Tổng hợp đề thi THPTQG môn Toán cực hay, có lời gi...

Câu 1 : Thể tích khối nón có bán kính bằng 2a và chiều cao bằng 3a là:

A. $2 {πa}^{3}$
B. $4 {πa}^{3}$
C. $12 {πa}^{3}$
D. ${πa}^{3}$

Câu 2 : Phương trình $2 \cos^{2} x + \cos x - 3 = 0$ có nghiệm là

A. $\frac{π}{2} + k π$
B. $k 2 π$
C. $\frac{π}{2} + k 2 π; x = \arcsin \frac{3}{2} + k 2 π$
D. $k π$
Câu 3 : Cho tam giác ABC vuông tại A, có $A B = a, B C = a \sqrt{10}$ . Thể tích khối nón khi quay tam giác ABC quanh trục AC là:

A. $3 {πa}^{3}$
B. $9 {πa}^{3}$
C. ${πa}^{3}$
D. $10 {πa}^{3}$
Câu 4 : Tính $P = \log_{2} 16 + \log_{\frac{1}{4}} 64 . \log_{\sqrt{2}} 2$

A. P = -2
B. P = 10
C. P = 1
D. P = -1
Câu 5 : Số hạng chính giữa trong khai triển ${(3 x + 2 y)}^{4}$ là

A. $36 C_{4}^{2} x^{2} y^{2}$
B. $4 {(3 x)}^{2} {(2 y)}^{2}$
C. $6 C_{4}^{2} x^{2} y^{2}$
D. $C_{4}^{2} x^{2} y^{2}$

Câu 6 : Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn là AD. Gọi M là trung điểm của SA, N là giao điểm của cạnh SB và mặt phẳng (MCD) Mệnh đề nào sau đây đúng?

A. MN và SD cắt nhau
B. MN và CD cắt nhau
C. MN và CD song song với nhau
D. MN và SC cắt nhau
Câu 7 : Tính giới hạn $M = \lim_{x \to - 1} \frac{x^{3} + 1}{x + 1}$

A. M = 0
B. M = -1
C. M = 1
D. M = 3
Câu 8 : Sự tăng trưởng của một loài vi khuẩn tuân theo công thức $N = A . e^{r t}$ trong đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng (r > 0) và t là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu có 250 con và sau 12 giờ là 1500 con. Hỏi sau bao lâu thì số lượng vi khuẩn tăng gấp 216 lần số lượng vi khuẩn ban đầu?

A. 48 giờ
B. 24 giờ
C. 60 giờ
D. 36 giờ
Câu 9 : Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, $A B = 2 a, B C = a, A A' = 2 a \sqrt{3}$ .Tính theo a thể tích khối trụ ABC.A'B'C'

A. $\frac{2 a^{3} \sqrt{3}}{3}$
B. $\frac{a^{3} \sqrt{3}}{3}$
C. $4 a^{3} \sqrt{3}$
D. $2 a^{3} \sqrt{3}$

Câu 10 : Cho các số tự nhiên n, k thỏa mãn $0 \leq k \leq n$ . Trong các đẳng thức sau, đẳng thức nào đúng.

A. $A_{n}^{k} = \frac{n!}{k!}$
B. $C_{n + 1}^{k} = C_{n + 1}^{n - k}$
C. $C_{n}^{k} + C_{n}^{k + 1} = C_{n + 1}^{k + 1}$
D. $P_{n} = \frac{n!}{(n - k)!}$
Câu 11 : Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AD, BC. Gọi G là trọng tâm $∆ B C D$ Khi đó, giao điểm của đường thẳng MG và mặt phẳng (ABC) là giao điểm của đường thẳng MG và đường thẳng

A. BC
B. AC
C. AN
D. AB
Câu 12 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f (x) = 2 x^{3} - 3 x^{2} - 12 x + 10$ trên đoạn [-3;3] là

A. $\underset{[- 3; 3]}{m a x} f (x) = 1; \underset{[- 3; 3]}{m i n} f (x) = - 35$
B. $\underset{[- 3; 3]}{m a x} f (x) = 1; \underset{[- 3; 3]}{m i n} f (x) = - 10$
C. $\underset{[- 3; 3]}{m a x} f (x) = 17; \underset{[- 3; 3]}{m i n} f (x) = - 10$
D. $\underset{[- 3; 3]}{m a x} f (x) = 17; \underset{[- 3; 3]}{m i n} f (x) = - 35$
Câu 13 : Trong các dãy số cho bởi công thức truy hồi sau, hãy chọn dãy số là cấp số nhân

A. $\{\begin{cases} u_{1} = 2 \\ u_{n + 1} = {u_{n}}^{2} \end{cases}$
B. $\{\begin{cases} u_{1} = - 3 \\ u_{n + 1} = u_{n} + 1 \end{cases}$
C. $\{\begin{cases} u_{1} = - 1 \\ u_{n + 1} = 3 u_{n} \end{cases}$
D. $\{\begin{cases} u_{1} = 3 \\ u_{n + 1} = 2^{n} . u_{n} \end{cases}$

Câu 14 : Hàm số nào dưới đây là hàm số chẵn?

A. $y = \sin 2 x + \sin 4 x$
B. $y = c o s x - \sin^{4} x + 2017$
C. $y = t a n x + c o t x$
D. $y = x \cos^{2} x + x^{2}$
Câu 15 : Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm $∆ A B D, ∆ A B C$ . Tìm mệnh đề đúng

A. Hai đường thẳng IJ, CD chéo nhau
B. Đường thẳng IJ cắt CD
C. Đường thẳng IJ cắt mặt phẳng (BCD)
D. Đường thẳng IJ//CD
Câu 16 : Cấp số cộng $(u_{n})$ có $\{\begin{cases} u_{1} + u_{3} = 8 \\ 2 u_{2} + 3 u_{4} = 32 \end{cases}$ . Khi đó, số hạng đầu tiên là

A. 8
B. $\frac{3}{2}$
C. 2
D. $\frac{22}{3}$
Câu 17 : Giải phương trình ${(4 + \sqrt{15})}^{2 x^{2} - 5 x} = {(4 - \sqrt{15})}^{6 - 2 x}$

A. $x = \frac{3}{2}; x = 2$
B. $x = \frac{3}{2}; x = - 2$
C. $x = - \frac{3}{2}; x = - 3$
D. $x = - \frac{3}{2}; x = 2$

Câu 18 : Cho cấp số cộng có $u_{4} = - 12, d = 3$ Khi đó tổng của 16 số hạng đầu tiên của cấp số cộng là

A. -24
B. 24
C. -26
D. 26
Câu 19 : Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD, E là trung điểm của cạnh SA, F, G là các điểm thuộc cạnh SC, AB (F không là trung điểm của SC). Thiết diện của hình chóp cắt bởi mặt phẳng (EFG) là:

A. Lục giác
B. Tứ giác
C. Ngũ giác
D. Tam giác
Câu 20 : Cho hàm số $y = \frac{3 - 4 x}{x + 1}$ có đồ thị (C) Trong các khẳng định sau, khẳng định nào đúng?

A. (C) có tiệm cận ngang là đường thẳng y = 4
B. (C)có tiệm cận đứng là đường thẳng x = -1
C. (C) không có tiệm cận
D. (C) có tiệm cận đứng là đường thẳng x = -4
Câu 21 : Cho hàm số f(x) có đồ thị như hình vẽ bên. Xác định tất cả các giá trị của tham số m để phương trình $|f (x)| = m$ có 6 nghiệm thực phân biệt

A. m > 4
B. 0 < m < 4
C. 0 < m < 3
D. 3 < m < 4

Câu 22 : Cho hình trụ có đường kính đáy là 8, đường sinh 10. Thể tích khối trụ là:

A. 160
B. $160 π$
C. $\frac{160}{3} π$
D. $640 π$
Câu 23 : Cho hàm số $y = f (x) = - 2 x^{3} + 3 x^{2} + 12 x - 5$ Mệnh đề nào dưới đây sai?

A. f(x) nghịch biến trên khoảng $(1; + \infty)$
B. f(x)đồng biến trên khoảng $(- 1; 1)$
C. f(x)đồng biến trên khoảng $(0; 2)$
D. f(x) nghịch biến trên khoảng $(- \infty; - 3)$
Câu 24 : Cho a, b là các số thực dương, thỏa mãn $a^{\frac{3}{4}} > a^{\frac{4}{3}}$ và $\log_{b} \frac{1}{2} < \log_{b} \frac{2}{3}$ Mệnh đề nào dưới đây đúng?

A. a > 1,0 < b < 1
B. 0 < a < 1,b > 1
C. 0 < a < 1,0 < b < 1
D. a > 1,b > 1
Câu 25 : Cho hàm số y = f(x) xác định trên khoảng (-2;-1) và có $\lim_{x \to 2^{-}} f (x) = 2, \lim_{x \to 1^{-}} f (x) = - \infty$ . Hỏi khẳng định nào dưới đây là khẳng định đúng?

A. Đồ thị hàm số f(x) có đúng một tiệm cận ngang là đường thẳng y = 2
B. Đồ thị hàm số f(x) có đúng hai tiệm cận ngang là các đường thẳng y = 2 và y = -1
C. Đồ thị hàm số f(x) có đúng một tiệm cận đứng là đường thẳng x = -1
D. Đồ thị hàm số f(x) có đúng hai tiệm cận đứng là các đường thẳng x = -2 và x = -1

Câu 26 : Cho hàm số $y = {(\frac{1}{10})}^{x}$ . Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số nghịch biến trên $ℝ$
B. Tập xác định của hàm số là $D = (0; + \infty)$
C. Tập giá trị của hàm số là $ℝ$
D. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng
Câu 27 : Tìm số hạng chứa $x^{4}$ trong khai triển ${(\frac{x}{3} - \frac{3}{x})}^{12}$

A. $\frac{55}{9}$
B. $\frac{55}{9} x^{4}$
C. $\frac{1}{81}$
D. $- \frac{1}{81}$
Câu 28 : Tìm tất cả các giả trị của tham số m sao cho đồ thị của hàm số $y = x^{3} - 3 x^{2} + (m + 2) x - m$ và đồ thị của hàm số y = 2x - 2 có 3 điểm chung phân biệt

A. m < 3
B. m > 3
C. m < 2
D. m > 2
Câu 29 : Cho hàm số $f (x) = \{\begin{cases} \frac{e^{a x} - 1}{x} k h i x \neq 0 \\ \frac{1}{2} k h i x = 0 \end{cases}$ với $a \neq 0$ . Tìm giá trị của a để hàm số f(x) liên tục tại $x_{0} = x$

A. $a = 1$
B. $a = \frac{1}{2}$
C. $a = - 1$
D. $a = - \frac{1}{2}$

Câu 30 : Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác cận tại A,AB=AC=2a, $\hat{C A B} = 120 °$ góc giữa (A'BC) và (ABC) là $45 °$ Thể tích lăng trụ là

A. $V = 2 a^{3} \sqrt{3}$
B. $V = a^{3} \sqrt{3}$
C. $V = \frac{a^{3} \sqrt{3}}{3}$
D. $V = \frac{a^{3} \sqrt{3}}{2}$
Câu 31 : Tìm số hạng không chứa x trong khai triển thành đa thức của ${(x \sqrt{x} + \frac{1}{x^{4}})}^{n}$ , với x > 0 nếu biết rằng $C_{n}^{2} - C_{n}^{1} = 44$

A. 165
B. 238
C. 485
D. 525
Câu 32 : Cho $m = \log_{2} 20$ . Tính $\log_{20} 5$ theo m được

A. $\frac{m - 2}{m}$
B. $\frac{m - 1}{m}$
C. $\frac{m}{m - 2}$
D. $\frac{m + 2}{m}$
Câu 33 : Cho hai hàm số $F (x) = (x^{2} + a x + b) e^{- x}$ và $f (x) = (- x^{2} + 3 x + 6) e^{- x}$ . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x).

A. a = 1,b = -7
B. a = -1,b = -7
C. a = -1,b = 7
D. a = 1,b = 7

Câu 34 : Cho hàm số $y = f (x) = a x^{3} + b x^{2} + c x + d$ Biết $f (x + 1) = x^{3} + 3 x^{2} + 3 x + 2$ hãy xác định biểu thức f(x)

A. $f (x) = x^{3} + 1$
B. $f (x) = x^{3} + 3 x + 2$
C. $f (x) = x^{3} + 3 x^{2}$
D. $f (x) = x^{3} + 3 x^{2} + 3 x + 1$
Câu 35 : Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;-4); B(1;-3;1); C(2;2;3). Tính đường kính l của mặt cầu (S) đi qua ba điểm trên và có tâm nằm trên mặt phẳng (Oxy)

A. $l = 2 \sqrt{13}$
B. $l = 2 \sqrt{41}$
C. $l = 2 \sqrt{26}$
D. $l = 2 \sqrt{11}$
Câu 36 : Cho hàm số $y = f (x) = a x^{3} + b x^{2} + c x + d$ có đồ thị như hĩnh vẽ sau

A. S = 1
B. S = 0
C. S = -2
D. S = -1
Câu 37 : Đồ thị hàm số $f (x) = \frac{1}{\sqrt{x^{2} - 4 x} - \sqrt{x^{2} - 3 x}}$ có bao nhiêu đường tiệm cận ngang?

A. 3
B. 1
C. 4
D. 2

Câu 38 : Cho hình chóp S.ABC có $S A ⊥ (A B C), S A = 2 a$ tam giác ABC cân tại A, $B C = 2 a \sqrt{2}, \cos \hat{A C B} = \frac{1}{3}$ . Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC

A. $S = \frac{97 {πa}^{2}}{\sqrt{3}}$
B. $S = \frac{97 {πa}^{2}}{4}$
C. $S = \frac{97 {πa}^{2}}{2}$
D. $S = \frac{97 {πa}^{2}}{5}$
Câu 39 : Trong mặt phẳng tọa độ Oxy, cho hai đường tròn $(C') : x^{2} + y^{2} + 2 (m - 2) y - 6 x + 12 + m^{2} = 0$ và $(C) : {(x + m)}^{2} + {(y - 2)}^{2} = 5$ . Vectơ $\vec{v}$ nào dưới đây là vectơ của phép tịnh tiến biến (C) thành (C')

A. $\vec{v} = (2; 1)$
B. $\vec{v} = (- 2; 1)$
C. $\vec{v} = (- 1; 2)$
D. $\vec{v} = (2; - 1)$
Câu 40 : Cho hàm số $f (x) = \{\begin{cases} \frac{x^{2} - 1}{x + 1} k h i x \neq - 1 \\ - 2 k h i x = - 1 \end{cases}$ . Trong các khẳng định sau, khẳng định nào sai

A. Hàm số f(x) liên tục trên khoảng $(- \infty; - 1)$
B. Hàm số không liên tục trên $ℝ$
C. Hàm số f(x) liên tục trên $ℝ$
D. Hàm số f(x) liên tục trên khoảng $(1; + \infty)$
Câu 41 : Gọi x, y là các số thực dương thỏa mãn điều kiện $\log_{9} x = \log_{6} x = \log_{4} (x + y)$ và biết rằng $\frac{x}{y} = \frac{- a + \sqrt{b}}{2}$ với a, b là các số nguyên dương. Tính giá trị a + b

A. a + b = 6
B. a + b = 11
C. a + b = 4
D. a + b = 8

Câu 42 : Tìm tất cả các giá trị thực của tham số m để bất phương trình $\log_{0, 02} [\log_{2} (3^{x} + 1)] > \log_{0, 02} m$ có nghiệm với mọi $x \in (- \infty; 0)$

A. m > 9
B. m < 2
C. 0 < m < 1
D. $m \geq 1$
Câu 43 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SA vuông góc với đáy (ABCD). Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng $α$ với $\tan α = \frac{\sqrt{10}}{5}$ . Tính góc giữa đường thẳng SO và mặt phẳng (ABCD).

A. $60 °$
B. $69, 3 °$
C. $90 °$
D. $45 °$
Câu 44 : Bổ dọc một quả dưa hấu ta được tiết diện là hình elip có trục lớn là 28cm, trục nhỏ 25cm. Biết cứ 31000cm dưa hấu sẽ làm được cốc sinh tố giá 20.000đ. Hỏi từ quả dưa như trên có thể thu được bao nhiêu tiền từ việc bán nước sinh tố? (Biết rằng bề dày vỏ dưa không đáng kể, kết quả đã được quy tròn)

A. 183.000đ
B. 180.000đ
C. 185.000đ
D. 190.000đ
Câu 45 : Cho dãy số $(u_{n})$ với $u_{n} = \frac{a n + 2}{n + 1}$ , a là tham số. Tìm tất cả các giá trị của a để dãy số là một dãy số tăng

A. a < 1
B. a > 1
C. a > 2
D. a < 2

Câu 46 : Tìm tất cả các giá trị thực của tham số m để hàm số $y = \sin^{3} x - 3 \cos^{2} x - m \sin x - 1$ đồng biến trên đoạn $[0; \frac{π}{2}]$

A. m > -3
B. $m \leq 0$
C. $m \leq - 3$
D. m > 0
Câu 47 : Cho hình chóp S.ABC có AB = BC = CA = a, SA = SB = SC = $a \sqrt{3}$ , M là điểm bất kì trong không gian. Gọi d là tổng các khoảng cách từ M đến tất cả các đường thẳng AB, BC, CA, SA, SB, SC. Giá trị nhỏ nhất của d bằng

A. $d = 2 a \sqrt{3}$
B. $\frac{a \sqrt{6}}{2}$
C. $a \sqrt{6}$
D. $\frac{a \sqrt{3}}{2}$
Câu 48 : Tìm m để phương trình $\log_{3}^{2} x - (m + 2) \log_{3} x + 3 m - 1 = 0$ có hai nghiệm $x_{1}, x_{2}$ thỏa mãn $x_{1} x_{2} = 27$

A. $m > 4 + 2 \sqrt{2}$
B. m = 1
C. m = 3
D. $m = \frac{28}{3}$
Câu 49 : Cho hàm số $y = f (x)$ xác định và có đạo hàm $f' (x)$ . Biết rằng hình bên là đồ thị của hàm số $f' (x)$ . Khẳng định nào sau đây là đúng về cực trị của hàm số $f (x)$

A. Hàm số f(x) đạt cực đại tại x = -1
B. Hàm số f(x) đạt cực tiểu tại x= 1
C. Hàm số f(x) đạt cực tiểu tại x = -2
D. Hàm số f(x) đạt cực đại tại x = -2

Câu 50 : Một hộp giấy hình hộp chữ nhật có thể tích 2dm³. Nếu tăng mỗi cạnh của hộp giấy thêm $\sqrt[3]{2}$ dm thì thể tích của hộp giấy là 16dm³. Hỏi nếu tăng mỗi cạnh của hộp giấy ban đầu lên $2 \sqrt[3]{2}$ dm thì thể tích hộp giấy mới là:

A. 32 $d m^{3}$
B. 54 $d m^{3}$
C. 64 $d m^{3}$
D. 72 $d m^{3}$
Câu 51 : Cho hàm số $y = f (x)$ liên tục trên $ℝ$ và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau

A. 1
B. 3
C. 4
D. 2
Câu 52 : Cho $a \in [\frac{1}{9}; 3]$ và M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P = 9 \log_{\frac{1}{3}}^{3} \sqrt[3]{a} - \log_{\frac{1}{3}} a^{3} + 1$ . Khi đó giá trị của $A = 5 m + 3 M$ gần giá trị nào nhất

A. -1,3
B. -1,5
C. -1,4
D. -1,2
Câu 53 : Cho hình lập phương ABCD.A’B’C’D’. Gọi M là điểm trên đường chéo CA’ sao cho $\vec{M C} = - 3 \vec{M A'}$ Tính tỉ số giữa thể tích $V_{1}$ của khối chóp M.ABCD và thể tích $V_{2}$ của khối lập phương?

A. $\frac{V_{1}}{V_{2}} = \frac{1}{3}$
B. $\frac{V_{1}}{V_{2}} = \frac{3}{4}$
C. $\frac{V_{1}}{V_{2}} = \frac{1}{9}$
D. $\frac{V_{1}}{V_{2}} = \frac{1}{4}$

Câu 54 : Cho mặt cầu (S) tâm O, bán kính R. Xét mặt phẳng (P) thay đổi cắt mặt cầu theo giao tuyến là đường tròn (C). Hình trụ (T) nội tiếp mặt cầu (S) có một đáy là đường tròn (C) và có chiều cao là $h (h > 0)$ . Tính h để khối trụ (T) có giá trị lớn nhất

A. $h = 2 R \sqrt{3}$
B. $h = \frac{2 R \sqrt{3}}{3}$
C. $h = R \sqrt{3}$
D. $h = \frac{R \sqrt{3}}{3}$
Câu 55 : Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho AN = 2DN. Đường thẳng qua N vuông góc với BN cắt BC tại K. Thể tích khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK là

A. $V = \frac{6}{7} {πa}^{3}$
B. $V = \frac{3}{2} {πa}^{3}$
C. $V = \frac{4}{3} {πa}^{3}$
D. $V = \frac{7}{6} {πa}^{3}$
Câu 56 : Cho hình cầu (O;R) hai mặt phẳng (P) và (Q) song song với nhau, cách đều O, đồng thời cắt khối cầu thành ba phần sao cho thể tích phần nằm giữa hai mặt phẳng bằng $\frac{13}{27}$ thể tích khối cầu .Tính khoảng cách giữa (P) và (Q).

A. $\frac{3 R}{2}$
B. $\frac{R}{3}$
C. $\frac{2 R}{3}$
D. $\frac{R}{2}$
Câu 57 : Hệ thức liên hệ giữa giá trị cực đại $y_{C D}$ và giá trị cực tiểu $y_{C T}$ của đồ thị hàm số $y = x^{3} - 2 x$ là:

A. $y_{C D} + y_{C T} = 0$
B. $y_{C T} = 2 y_{C D}$
C. $y_{C T} = y_{C D}$
D. $2 y_{C T} = 3 y_{C D}$

Câu 58 : Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x + 2y - 2z + 2 =0 và mặt cầu tâm I(1;4;1) bán kính R tiếp xúc với (P). Bán kính R là:

A. $R = \frac{7}{3}$
B. $R = 3$
C. $R = 1$
D. $R = 9$
Câu 59 : Tính $L = \lim_{x \to - \infty} (\sqrt{x^{2} + x + 1} + \sqrt[3]{x^{3} + 1})$ .

A. L = -0,5
B. L = $- \infty$
C. L = 0
D. L = 0,5
Câu 60 : Trong các phép biến hình sau, phép nào không phải là phép dời hình

A. Phép chiếu vuông góc lên một đường thẳng
B. Phép đối xứng trục
C. Phép đồng nhất
D. Phép vị tự tỉ số -1
Câu 61 : Cho số phức z = 5 +2i. Tìm phần thực và phần ảo của số phức z .

A. Phần thực bằng -5 và phần ảo bằng -2
B. Phần thực bằng 5 và phần ảo bằng 2
C. Phần thực bằng 5 và phần ảo bằng -2
D. Phần thực bằng 5 và phần ảo bằng -2i

Câu 62 : Tìm a để hàm số $y = \{\begin{cases} x^{2} + 1, x > 3 \\ a . x + 4, x \leq 3 \end{cases}$ liên tục tai điểm $x_{0} = 3$ ?

A. a = 1
B. a = 2
C. a = 4
D. a = 3
Câu 63 : Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;3;2); B(3;5;-4). Phương trình mặt phẳng trung trực của AB là:

A. x + y - 3z + 9 = 0
B. x + y - 3z + 2 = 0
C. $\frac{x - 3}{1} = \frac{y - 5}{1} = \frac{z + 4}{- 3}$
D. x + y - 3z - 9 = 0
Câu 64 : Chỉ ra mệnh đề sai trong các mệnh đề sau:

A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Cho hai đường thẳng vuông góc với nhau, mặt phẳng nào vuông góc với đường thẳng này thì song song với đường thẳng kia.
C. Cho hai đường thẳng song song với nhau, mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
D. Cho hai mặt phẳng song song với nhau, đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
Câu 65 : Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Kết quả nào sau đây là đúng?

A. (AFD)//(BEC)
B. EC//(ABF)
C. (ABD)//(EFC)
D. AD//(BEF)

Câu 66 : Cho hình chóp S.ABC có $B S C = 120 °, C S A = 60 °, A S B = 90 °, S A = S B = S C$ . Gọi I là hình chiếu vuông góc của S lên mp (ABC). Chọn khẳng định đúng trong các khẳng định sau?

A. I là trung điểm của AB
B. I là trung điểm của BC
C. I là trọng tâm của tam giác ABC
D. I là trung điểm của AC
Câu 67 : Cho hình chóp S.ABCDcó đáy ABCD là hình vuông cạnh a, SA $⊥$ (ABCD), SA = $a \sqrt{6}$ . Gọi là góc giữa SC và mp (ABCD). Chọn khẳng định đúng trong các khẳng định sau?

A. $\cos α = \frac{\sqrt{3}}{3}$
B. $α = 60 °$
C. $α = 45 °$
D. $α = 30 °$
Câu 68 : Cho hàm số $y = \frac{2 x + 1}{x - 1}$ . Số tiệm cận của đồ thị hàm số là:

A. 3
B. 2
C. 1
D. 0
Câu 69 : Cho hình chữ nhật ABCD có AB = 3AD. Quay hình chữ nhật ABCD lần lượt quanh AD và AB ta thu được hai hình trụ tròn xoay tương ứng có thể tích $V_{1}; V_{2}$ . Hỏi hệ thức nào sau đây là đúng?

A. $V_{2} = 3 V_{1}$
B. $V_{2} = V_{1}$
C. $V_{1} = 3 V_{2}$
D. $V_{1} = 9 V_{2}$

Câu 70 : Cho hai số phức $z_{1} = 4 + i$ và $z_{2} = 1 - 3 i$ . Tính môđun của số phức $z_{1} - z_{2}$ .

A. $|z_{1} - z_{2}| = \sqrt{17} - \sqrt{10}$
B. $|z_{1} - z_{2}| = \sqrt{13}$
C. $|z_{1} - z_{2}| = 25$
D. $|z_{1} - z_{2}| = 5$
Câu 71 : Tìm nguyên hàm của hàm của hàm số $f (x) = {(2 x - 1)}^{2}$ .

A. $\int f (x) d x = \frac{{(2 x - 1)}^{3}}{6} + C$
B. $\int f (x) d x = \frac{{(2 x - 1)}^{3}}{3} + C$
C. $\int f (x) d x = 4 (2 x - 1) + C$
D. $\int f (x) d x = 2 (2 x - 1) + C$
Câu 72 : Ba người cùng đi săn A, B, C độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A, B, C tương ứng với 0,7; 0,6; 0,5. Tính xác suất để có ít nhất một xạ thủ bắn trúng?

A. 0,75
B. 0,45
C. 0,94
D. 0,80
Câu 73 : Cho a, b, c là các số thực dương, $a \neq 1$ . Xét các mệnh đề sau:

A. 3
B. 2
C. 1
D. 0

Câu 74 : Có 10 chiếc bút, 15 cái thước, 5 cái tẩy, các đồ vật này phân biệt. Chọn 1 đồ vật trong số các đồ vật trên. Hỏi có bao nhiêu cách chọn?

A. 30
B. 10!.15!.5!
C. 30!
D. 25!
Câu 75 : Cho hàm số y = f(x). Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ $x_{0}$ có hệ số góc là:

A. $k = f' (x_{0}) . (x - x_{0}) + f (x_{0})$
B. $k = f' (x_{0}) + f (x_{0})$
C. $k = f (x_{0})$
D. $k = f' (x_{0})$
Câu 76 : Giá trị lớn nhất của hàm số y = 3sin3x - 4cos3x + 5 ?

A. 5
B. 10
C. 4
D. 12
Câu 77 : Cho x = log2017, y = ln2017. Hỏi quan hệ nào sau đây giữa x và y là đúng?

A. $\frac{1}{x} + \frac{1}{y} = \frac{e}{10}$
B. $\frac{x}{y} = \frac{10}{e}$
C. $10^{y} = e^{x}$
D. $10^{x} = e^{y}$

Câu 78 : Kí hiệu $z_{1}, z_{2}, z_{3}, z_{4}$ là bốn nghiệm phức của phương trình $z^{4} - 3 z^{2} - 4 = 0$ . Tính $T = |z_{1} + z_{2} + z_{3} + z_{4}|$

A. T = 3
B. T = 0
C. T = 4 + $\sqrt{2}$
D. T = 4
Câu 79 : Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f (x) = x + \frac{9}{x}$ trên đoạn [1;4]. Tính hiệu M - m.

A. $M - m = \frac{1}{4}$
B. $M - m = \frac{15}{4}$
C. $M - m = 16$
D. $M - m = 4$
Câu 80 : Cho số phức z thỏa mãn (2 - i)z = (2 + i)(1 - 3i). Gọi M là điểm biểu diễn của z. Khi đó tọa độ điểm M là.

A. M(3;1)
B. M(3;-1)
C. M(1;3)
D. M(1;-3)
Câu 81 : Một hãng dược phẩm cần một số lọ đựng thuốc dạng hình trụ với dung tích $16 π {cm}^{3}$ . Tính bán kính đáy R của lọ để ít tốn nguyên liệu sản xuất lọ nhất.

A. $R = 2 c m$
B. $R = 1, 6 c m$
C. $R = π c m$
D. $R = \frac{16}{π} c m$

Câu 82 : Cho khối chóp S.ABCD có đáy ABCD là hình thoi. Gọi O là giao điểm của AC và BD. Tỉ số thể tích giữa khối chóp S.ABCD và S.AOB là:

A. $\frac{1}{2}$
B. $\frac{1}{4}$
C. 4
D. 2
Câu 83 : Biết F(x) là nguyên hàm của hàm số $f (x) = \frac{3 x^{4} - 2 x^{3} - 1}{x^{2}}$ và F(1) + 2F(2) = 40. Tính F(-1).

A. 8
B. 7
C. -8
D. 0
Câu 84 : Tìm tập nghiệm S của bất phương trình ${(\frac{1}{3})}^{x + 1} - 3 > 0$

A. $S = (- \infty; - 2)$
B. $S = (- 1; + \infty)$
C. $S = (1; + \infty)$
D. $S = (- 2; + \infty)$
Câu 85 : Cho hàm số $y = x^{4} - x^{2} - 12$ có đồ thị (C). Tìm số giao điểm của (C) và trục hoành

A. 0
B. 3
C. 2
D. 4

Câu 86 : Một khối nón có diện tích toàn phần bằng $10 π$ và diện tích xung quanh bằng $6 π$ . Tính thể tích V của khối nón đó.

A. $V = 4 π \sqrt{5}$
B. $V = \frac{4 π \sqrt{5}}{3}$
C. $V = 12 π$
D. $V = 4 π$
Câu 87 : Tìm tập nghiệm của phương trình $\log_{2} (x - 2) + \log_{2} (x + 1) = 2$

A. $S = \{- 2; 3\}$
B. $S = \{3\}$
C. $S = \{\frac{1 - \sqrt{17}}{2}; \frac{1 + \sqrt{17}}{2}\}$
D. $S = \emptyset$
Câu 88 : Trong mặt phẳng Oxy, cho điểm A(2;-1). Ảnh của điểm A qua phép vị tự tâm O tỉ số k = 2 có tọa độ là:

A. $A' (4; 2)$
B. $A' (4; - 2)$
C. $A' (2; 1)$
D. $A' (- 4; - 2)$
Câu 89 : Đồ thị hàm số $y = \frac{x + 1}{x^{2} - 4 |x| + 3}$ có bao nhiêu đường tiệm cận đứng?

A. 1
B. 2
C. 3
D. 4

Câu 90 : Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm các tam giác ABC và ABD. Trong các mệnh đề sau, mệnh đề nào đúng?

A. IJ//AB
B. IJ//DC
C. IJ//BD
D. IJ//AC
Câu 91 : Cho số phức z có phần ảo âm, gọi $w = 2 z + |z - \bar{z}| i$ . Khi đó khẳng định nào sau đây về w là đúng?

A. w là số thực
B. w có phần thực bằng 0
C. w có phần ảo âm
D. w có phần ảo dương
Câu 92 : Cho hình nón có bán kính đáy bằng 2a và độ dài đường sinh $l = \frac{5 a}{2}$ . Diện tích toàn phần của hình nón bằng

A. $10 {πa}^{2}$
B. $11 {πa}^{2}$
C. $3 {πa}^{2}$
D. $9 {πa}^{2}$
Câu 93 : Cho hàm số f(x) có bảng biến thiên như hình vẽ bên. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?

A. 2
B. 3
C. 1
D. 2

Câu 94 : Cho a là số thực dương. Mệnh đề nào sau đây đúng ?

A. $\log_{3} \frac{a^{2}}{\sqrt{3}} = 2 \log_{3} a - 2$
B. $\log_{3} \frac{a^{2}}{\sqrt{3}} = 2 \log_{3} a + 2$
C. $\log_{3} \frac{a^{2}}{\sqrt{3}} = 2 \log_{3} a - \frac{1}{2}$
D. $\log_{3} \frac{a^{2}}{\sqrt{3}} = 2 \log_{3} a + \frac{1}{2}$
Câu 95 : Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , SD tạo với mặt phẳng (SAC) một góc bằng $30 °$ . Tính thể tích V của hình chóp S.ABCD.

A. $V = \frac{\sqrt{6} a^{3}}{6}$
B. $V = \frac{a^{3}}{3}$
C. $V = \frac{\sqrt{6} a^{3}}{2}$
D. $V = \frac{a^{3}}{6}$
Câu 96 : Cho số thực x lớn hơn 1 và ba số thực dương a, b, c khác 1 thỏa mãn điều kiện $\log_{a} x > \log_{b} x > 0 > \log_{c} x$ . Mệnh đề nào sau đây đúng ?

A. c > a > b
B. b > a > c
C. c > b > a
D. a > b > c
Câu 97 : Hàm số $y = \frac{2 \sin x + 1}{1 - c o s x}$ xác định khi:

A. $x \neq \frac{π}{2} + k 2 π$
B. $x \neq \frac{π}{2} + k π$
C. $x \neq k 2 π$
D. $x \neq k π$

Câu 98 : Cho 6 chữ số 2, 3, 4, 5, 6, 7. Hỏi có bao nhiêu số gồm 3 chữ số được lập thành từ 6 chữ số đó?

A. 36
B. 18
C. 216
D. 256
Câu 99 : Phương trình $s i n x - m = 0$ vô nghiệm khi m là:

A. $- 1 \leq m \leq 1$
B. $[\begin{array}{l} m < - 1 \\ m > 1 \end{array}$
C. m < -1
D. m > 1
Câu 100 : Cho hai mặt phẳng (P)và (Q)song song với nhau. Mệnh đề nào sau đây sai?

A. $d \subset (P)$ và $d' \subset (Q)$ thì $d / / d'$
B. Mọi đường thẳng đi qua điểm $A \in (P)$ và song song với (Q) đều nằm trong (P)
C. Nếu đường thẳng $a \subset (Q)$ thì a // (P)
D. Nếu đường thẳng $∆$ cắt (P) thì $∆$ cũng cắt (Q)
Câu 101 : Phương trình $\cos x = \frac{\sqrt{3}}{2}$ có nghiệm thỏa mãn $0 \leq x \leq π$ là:

A. $x = \frac{π}{3} + k 2 π$
B. $x = \frac{π}{6} + k 2 π$
C. $x = \frac{π}{3}$
D. $x = \frac{π}{6}$

Câu 102 : Cho hình chóp S.ABC có đáy ABC vuông tại B, SA vuông góc với đáy ABC. Khẳng định nào dưới đây sai?

A. $S A ⊥ B C$
B. $S B ⊥ A C$
C. $S A ⊥ A B$
D. $S B ⊥ B C$
Câu 103 : Điều kiện để phương trình $3 \sin x + m \cos x = 5$ vô nghiệm là:

A. m > 4
B. m < -4
C. -4 < m < 4
D. $[\begin{array}{l} m \leq - 4 \\ m \geq 4 \end{array}$
Câu 104 : Hình chóp S.ABC có đáy là tam giác ABC vuông tại A, có SA vuông góc với mặt phẳng (ABC) và có SA = a, AB = b, AC = a. Mặt cầu đi qua các đỉnh có bán kính r bằng:

A. $\frac{1}{2} \sqrt{a^{2} + b^{2} + c^{2}}$
B. $2 \sqrt{a^{2} + b^{2} + c^{2}}$
C. $\frac{2 (a + b + c)}{3}$
D. $\sqrt{a^{2} + b^{2} + c^{2}}$
Câu 105 : Cho hàm số $y = \frac{2 x + 3}{x + 2}$ có đồ thị (C) và đường thẳng d ; y = x + m. Với giá trị nào của tham số m thì d cắt (C) tại hai điểm phân biệt?

A. m < -2
B. m < 2 hoặc m > 6
C. 2 < m < 6
D. m < -6

Câu 106 : Tìm tất cả các giá trị của a sao cho $l i m \frac{a . 2^{n} - 3}{a + 2^{n + 1}} = 1$

A. a = 1
B. a = 2
C. a = -3
D. $a \neq 0$
Câu 107 : Khẳng định nào sau đây là khẳng định đúng?

A. Hai đường thẳng phân biệt không song song thì chéo nhau
B. Hai đường thẳng không có điểm chung thì chéo nhau
C. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau
D. Hai đường thẳng chéo nhau thì không có điểm chung
Câu 108 : Tập giá trị của hàm số $y = \sin 2 x + 3$ là:

A. [2;3]
B. [-2;3]
C. [2;4]
D. [0;1]
Câu 109 : Cho tích phân $I = \int_{0}^{\frac{π}{4}} \frac{\sin 2 x d x}{\cos^{4} x + \sin^{4} x}$ . Nếu đặt t = cos2x thì mệnh đề nào sau đây đúng?

A. $I = \int_{0}^{1} \frac{- d t}{t^{2} + 1}$
B. $I = \int_{0}^{1} \frac{d t}{t^{2} + 1}$
C. $I = \frac{1}{2} \int_{0}^{1} \frac{d t}{t^{2} + 1}$
D. $I = \int_{0}^{1} \frac{2 d t}{t^{2} + 1}$

Câu 110 : Gọi S là diện tích hình phẳng giới hạn bởi đồ thị $(C) : y = \frac{2 x - 1}{x + 1}$ , tiệm cận ngang của (C) trục tung và đường thẳng x = a(a > 0). Tìm a để S = ln2017.

A. $a = \sqrt[3]{2017} - 1$
B. $a = \frac{2017}{3} - 1$
C. $a = 2016$
D. $a = \sqrt{2017} - 1$
Câu 111 : Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-1;3) và hai đường thẳng, $d_{1} : \frac{x - 4}{1} = \frac{y + 2}{4} = \frac{z - 1}{- 2}, d_{2} = \frac{x - 2}{1} = \frac{y + 1}{- 1} = \frac{z - 1}{1}$ . Viết phương trình đường thẳng d đi qua A, vuông góc với đường thẳng $d_{1}$ và cắt đường thẳng $d_{2}$ .

A. $d : \frac{x - 4}{4} = \frac{y + 1}{1} = \frac{z - 3}{4}$
B. $d : \frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z - 3}{3}$
C. $d : \frac{x - 1}{2} = \frac{y + 1}{- 1} = \frac{z - 3}{- 1}$
D. $d : \frac{x - 1}{- 2} = \frac{y + 1}{2} = \frac{z - 3}{3}$
Câu 112 : Trong mặt phẳng Oxy cho điểm M(1;-2). Tọa độ ảnh của điểm M qua phép tịnh tiến theo vectơ $\vec{v} (3; - 2)$ là:

A. M'(-2;4)
B. M'(4;-4)
C. M'(4;4)
D. M'(-2;0)
Câu 113 : Cho khối chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng $a \sqrt{3}$ . Tính thể tích V của khối chóp đó theo a:

A. $V = \frac{a^{3} \sqrt{2}}{3}$
B. $V = \frac{a^{3} \sqrt{3}}{6}$
C. $V = \frac{a^{3} \sqrt{10}}{6}$
D. $V = \frac{a^{3}}{2}$

Câu 114 : Trên mặt phẳng tọa độ Oxy, xét tam giác vuông OAB với A chạy trên trục hoành và có hoành độ dương; B chạy trên trục tung và có tung độ âm sao cho OA + OB = 1. Hỏi thể tích lớn nhất của vật thể tạo thành khi quay tam giác OAB quanh trục Oy bằng bao nhiêu?

A. $\frac{4 π}{81}$
B. $\frac{25 π}{27}$
C. $\frac{9 π}{4}$
D. $\frac{17 π}{9}$
Câu 115 : Đặt $a = \log_{3} 5, b = \log_{4} 5$ . Hãy biểu diễn $\log_{15} 10$ theo a và b.

A. $\log_{15} 10 = \frac{a^{2} - a b}{a b + b}$
B. $\log_{15} 10 = \frac{a + 2 a b}{2 a b + 2 b}$
C. $\log_{15} 10 = \frac{a + 2 a b}{2 a b}$
D. $\log_{15} 10 = \frac{a^{2} - a b}{a b}$
Câu 116 : Một hình lập phương cạnh bằng a nội tiếp khối cầu $(S_{1})$ và ngoại tiếp khối cầu $(S_{2})$ , gọi $V_{1}$ và $V_{2}$ lần lượt là thể tích của các khối $(S_{1})$ và $(S_{2})$ . Tính tỉ số $k = \frac{V_{1}}{V_{2}}$ .

A. $k = \frac{1}{2 \sqrt{2}}$
B. $k = \frac{1}{3 \sqrt{3}}$
C. $k = 2 \sqrt{2}$
D. $3 \sqrt{3}$
Câu 117 : Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AA' = 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là $\frac{9 {πa}^{3}}{2}$ . Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.

A. $V = \frac{9 a^{3}}{4}$
B. $V = 4 a^{3}$
C. $V = \frac{4 a^{3}}{3}$
D. $V = 2 a^{3}$

Câu 118 : Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;0;0), B(0;3;0), C(0;0;2), D(1;3;-2). Hỏi có tất cả bao nhiêu mặt phẳng cách đều 5 điểm O, A, B, C, D (O là gốc tọa độ )?

A. 5 mặt phẳng
B. 4 mặt phẳng
C. Có vô số mặt phẳng
D. 7 mặt phẳng
Câu 119 : Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số $y = \frac{2 x - \sqrt{(m - 1) x^{2} + 1}}{x - 1}$ có đúng hai tiệm cận ngang?

A. m = 1
B. $m \in (1; 4) \cup (4; + \infty)$
C. m < 1
D. m > 1
Câu 120 : Các giá trị của tham số m để phương trình $12^{x} + (4 - m) . 3^{x} - m = 0$ có nghiệm thực khoảng (-1;0) là:

A. $m \in (\frac{17}{16}; \frac{5}{2})$
B. $m \in [2; 4]$
C. $m \in (\frac{5}{2}; 6)$
D. $m \in (1; \frac{5}{2})$
Câu 121 : Một hộp chứa 3 quả cầu trắng và 2 quả cầu đen. Lấy ngẫu nhiên đồng thời hai quả. Xác suất để lấy được cả hai quả trắng là:

A. $\frac{2}{10}$
B. $\frac{4}{10}$
C. $\frac{5}{10}$
D. $\frac{3}{10}$

Câu 122 : Cho a, b là các số thực dương thỏa mãn $a \neq 1, \sqrt{a} \neq b$ và $\log_{a} b = \sqrt{2}$ . Tính $P = \log_{\frac{b}{\sqrt{a}}} \sqrt{\frac{a}{b}}$ .

A. $P = \frac{1 - \sqrt{2}}{2 \sqrt{2} - 1}$
B. $P = \frac{1 + \sqrt{2}}{2 \sqrt{2} + 1}$
C. $P = \frac{1 - \sqrt{2}}{2 \sqrt{2} + 1}$
D. $P = \frac{1 + \sqrt{2}}{2 \sqrt{2} - 1}$
Câu 123 : Hỏi có bao nhiêu số nguyên m để hàm số $y = \frac{1}{3} (m - 2) x^{3} + (m - 2) x^{2} - 2 x + 4$ nghịch biến trên khoảng ?

A. 0
B. 3
C. 1
D. 2
Câu 124 : Cho hình lập phương ABCD.A'B'C'D'. Gọi M là điểm trên đường chéo CA' sao cho $\vec{M C} = - 3 \vec{M A'}$ . Tính tỉ số giữa thể tích $V_{1}$ của khối chóp M.ABCD và thể tích $V_{2}$ của khối lập phương.

A. $\frac{V_{1}}{V_{2}} = \frac{1}{3}$
B. $\frac{V_{1}}{V_{2}} = \frac{3}{4}$
C. $\frac{V_{1}}{V_{2}} = \frac{1}{9}$
D. $\frac{V_{1}}{V_{2}} = \frac{1}{4}$
Câu 125 : Cho $\log_{b} a = x; \log_{b} c = y$ . Hãy biểu diễn $\log_{a^{2}} (\sqrt[3]{b^{5} c^{4}})$ theo x và y:

A. $\frac{5 + 4 y}{6 x}$
B. $\frac{20 y}{3 x}$
C. $\frac{5 + 3 y^{4}}{3 x^{2}}$
D. $2 x + \frac{20 y}{3}$

Câu 126 : Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng $60 °$ . Tính thể tích V của khối tứ diện ABCD theo a:

A. $V = \frac{a^{3}}{8}$
B. $V = \frac{a^{3} \sqrt{3}}{16}$
C. $V = \frac{a^{3} \sqrt{2}}{8}$
D. $V = \frac{a^{3} \sqrt{2}}{12}$
Câu 127 : Cho các số thực a,b thỏa mãn a > b > 1. Chọn khẳng định sai trong các khẳng định sau:

A. $\log_{a} b > \log_{b} a$
B. $\log_{a} b < \log_{b} a$
C. $\ln a > \ln b$
D. $\log_{\frac{1}{2}} (a b) < 0$
Câu 128 : Các thành phố A,B,C,D được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?

A. 10
B. 9
C. 24
D. 18
Câu 129 : Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Gọi M là trung điểm A'B' là trung điểm. Tính thể tích của khối tứ diện ADMN

A. $V = \frac{a^{3}}{3}$
B. $V = \frac{a^{3}}{12}$
C. $V = \frac{a^{3}}{6}$
D. $V = \frac{a^{3}}{2}$

Câu 130 : Xét một phép thử có không gian mẫu $Ω$ và A là một biến cố của phép thử đó. Phát biểu nào dưới đây là sai?

A. P(A) = 0 khi và chỉ khi A là chắc chắn
B. $0 \leq P (A) \leq 1$
C. Xác suất của biến cố A là số $P (A) = \frac{n (A)}{n (Ω)}$
D. $P (A) = 1 - P (A)$
Câu 131 : Cho bốn điểm A,B,C,D không cùng nằm trong một mặt phẳng. Trên AB,AD lần lượt lấy các điểm M và N sao cho MN cắt BD tại I. Điểm I không thuộc mặt phẳng nào sau đây:

A. (ACD)
B. (CMN)
C. (BCD)
D. (ABD)
Câu 132 : Cho đường tròn tâm O đường kính AB = 8. Trên AB lấy 2 điểm M, N đối xứng nhau qua O sao cho MN = 4. Qua M, N kẻ 2 dây cung PQ và EF cùng vuông góc với AB. Tính diện tích S phần giới hạn bới đường tròn và 2 dây cung PQ, EF (phần chứa điểm O ).

A. $S = \frac{16}{3} π + 8 \sqrt{3}$
B. $S = 8 π + 5$
C. $S = 12 π - 7$
D. $S = 6 π + 8 \sqrt{3}$
Câu 133 : Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp S.ABCD cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB,CD để thiết diện đó là hình bình hành?

A. AB = 3CD
B. AB = 2CD
C. CD = 2AB
D. CD = 3AB

Câu 134 : Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng

A. $\frac{(3 + 2 \sqrt{3}) {πR}^{2}}{3}$
B. $\frac{(3 + 2 \sqrt{3}) {πR}^{2}}{2}$
C. $\frac{(3 + 2 \sqrt{2}) {πR}^{2}}{2}$
D. $\frac{(3 + 2 \sqrt{2}) {πR}^{2}}{3}$
Câu 135 : Gọi T là tập hợp các số phức z thỏa mãn $|z - i| \geq 3$ và $|z - 1| \leq 5$ . Gọi $z_{1}, z_{2} \in T$ lần lượt là các số phức có môđun nhỏ nhất và lớn nhất. Tìm số phức $z_{1} + 2 z_{2}$ .

A. 12 - 2i
B. -2 + 12i
C. 6 - 4i
D. 12 + 4i
Câu 136 : Cho hàm số y = f(x) liên tục trên $ℝ$ và hàm số $y = g (x) = x f (x^{2})$ có đồ thị trên đoạn [0;2] như hình vẽ bên. Biết diện tích miền được tô màu là $S = \frac{5}{2}$ , tính tích phân $I = \int_{1}^{4} f (x) d x$ .

A. $I = \frac{5}{4}$
B. $I = \frac{5}{2}$
C. $I = 5$
D. $I = 10$
Câu 137 : Một sân chơi cho trẻ em hình chữ nhật có chiều dài 100m và chiều rộng là 60m người ta làm một con đường nằm trong sân (như hình vẽ). Biết rằng viền ngoài và viền trong của con đường là hai đường Elip, Elip của đường viền ngoài có trục lớn và trục bé lần lượt song song với các cạnh hình chữ nhật và chiều rộng của mặt đường là 2m. Kinh phí của mỗi $m^{2}$ làm đường 600.000đồng. Tính tổng số tiền làm con đường đó. (Số tiền được làm tròn đến hàng nghìn).

A. 293.904.000
B. 283.904.000
C. 293.804.000
D. 294.053.072

Câu 138 : Khi tính giới hạn $\lim_{x \to - \infty} \frac{\sqrt{x^{2} - x} + 2 x}{3 - 4 |x|}$ ta được kết quả là một phân số tối giản $\frac{a}{b}, a \in ℤ, b \in ℤ, b \neq 0$ . Tính a + b?

A. a + b = 5
B. a + b = 7
C. a + b = -1
D. a + b = -3
Câu 139 : Cho hàm số $f (x) = \{\begin{cases} \sqrt{x - 1} + x k h i x \geq 1 \\ (m^{3} - 3 m + 3) x k h i x < 1 \end{cases}$ . Tìm tất cả các giá trị của tham số m để hàm số liên tục trên $ℝ$ ?

A. $m = 1; m = - 2$
B. $m = 1; m = 2$
C. $m = - 1; m = - 2$
D. $m = 1; m = 2$
Câu 140 : Cho hàm số f(x) xác định trên $ℝ$ và có đồ thị hàm số y = f '(x) là đường cong trong vẽ dưới đây.Mệnh đề nào dưới đây đúng ?

A. f(x) đồng biến trên khoảng (1;2)
B. f(x) nghịch biến trên khoảng (0;2)
C. f(x) đồng biến trên khoảng (-2;1)
D. f(x) nghịch biến trên khoảng (-1;1)
Câu 141 : Trong không gian với hệ tọa độ Oxyz cho ba điểm A(0;1;1), B(3;0;-1), C(0;21;-19) và mặt cầu $(S) : {(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 1$ . M(a;b;c) là điểm thuộc mặt cầu (S) sao cho biểu thức $T = 3 M A^{2} + 2 M B^{2} + M C^{2}$ đạt giá trị nhỏ nhất. Tính tổng a + b + c.

A. a + b + c = 0
B. a + b + c = 12
C. a + b + c = $\frac{12}{5}$
D. a + b + c = $\frac{15}{4}$

Câu 142 : Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 1, SA vuông góc với đáy, góc giữa mặt bên (SBC) và đáy bằng 60 $°$ . Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng bao nhiêu?

A. $\frac{43 π}{4}$
B. $\frac{43 π}{36}$
C. $\frac{43 π}{12}$
D. $\frac{4 {πa}^{3}}{16}$
Câu 143 : Gọi a, b, c là ba số thực khác 0 thay đổi và thỏa mãn điều kiện $3^{a} = 5^{b} = 15^{- c}$ . Tìm giá trị nhỏ nhất của biểu thức $P = a^{2} + b^{2} + c^{2} - 4 (a + b + c)$

A. $- 3 - \log_{5} 3$
B. -4
C. $- 2 - \sqrt{3}$
D. $- 2 - \log_{5} 3$
Câu 144 : Cho tam giác ABC có AB = 3,BC = 5,CA = 7. Tính thể tích của khối tròn xoay sinh ra là do hình tam giác ABC quay quanh đường thẳng AB:

A. $50 π$
B. $\frac{75 π}{4}$
C. $\frac{275 π}{8}$
D. $\frac{125 π}{8}$
Câu 145 : Tất cả các giá trị của tham số m để bất phương trình $(3 m + 1) . 12^{x} + (2 - m) 6^{x} + 3^{x} < 0$ có nghiệm đúng với mọi x > 0 là:

A. m > -2
B. m < -2
C. $m < \frac{1}{3}$
D. $- 2 < m < \frac{1}{3}$

Câu 146 : Cho $\int_{- 1}^{5} f (x) d x = 5, \int_{4}^{5} f (t) d t = - 2$ và $\int_{- 1}^{4} g (u) d u = \frac{1}{3}$ .Tính $\int_{- 1}^{4} (f (x) + g (x)) d x$ bằng.

A. $\frac{8}{3}$
B. $\frac{22}{3}$
C. $\frac{- 20}{3}$
D. $\frac{10}{3}$
Câu 147 : Cho khối hộpABCD.A'B'C'D' Gọi M là trung điểm của cạnh AB. Mặt phẳng (MB'D') chia khối hộp thành hai phần. Tính tỉ số thể tích hai phần đó.

A. $\frac{5}{12}$
B. $\frac{7}{17}$
C. $\frac{7}{24}$
D. $\frac{5}{17}$
Câu 148 : Cho biết sự tăng dân số được ước tính theo công thức $S = A . e^{N r}$ (trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau N năm, r là tỉ lệ tăng dân số hàng năm). Đầu năm 2010 dân số tỉnh Bắc Ninh là 1.038.229 người tính đến đầu năm 2015 dân số của tỉnh là 1.153.600 người. Hỏi nếu tỉ lệ tăng dân số hàng năm giữ nguyên thì đầu năm 2020 dân số của tỉnh nằm trong khoảng nào?

A. (1.281.600;1.281.700)
B. (1.281.800;1.281.900)
C. (1.281.900;1.282.000)
D. (1.281.700;1.281.800)
Câu 149 : Cho hình phẳng (H) giới hạn bởi các đường $y = \sqrt{\ln x}, y = 0, x = 1 v à x = k (k > 1)$ . Gọi $V_{k}$ là thể tích khối tròn xoay thu được khi quay hình (H) quanh trục Ox. Biết rằng $V_{k} = π$ , hãy chọn khẳng định đúng?

A. 3 < k < 4
B. 1 < k < 2
C. 2 < k < 3
D. 4 < k < 5

Câu 150 : Phần không gian bên trong của chai rượu có hình dạng như hình bên. Biết bán kính đáy bằng R = 4,5 cm bán kính cổ r = 1,5cm,AB = 4,5 cm, BC = 6,5cm, CD = 20cm. Thể tích phần không gian bên trong của chai rượu đó bằng:

A. $\frac{3321 π}{8} c m^{3}$
B. $\frac{7695 π}{16} c m^{3}$
C. $\frac{957 π}{2} c m^{3}$
D. $478 π c m^{3}$
Câu 151 : Lãi suất tiền gửi tiết kiệm của ngân hàng thời gian vừa qua liên tục thay đổi. Ông A gửi số tiền ban đầu là 10 triệu đồng với lãi suất 0,5%/tháng, chưa đầy nửa năm thì lãi suất tăng lên 1%/tháng trong vòng một quý (3 tháng) và sau đó lãi suất lại thay đổi xuống còn 0,8%/tháng. Ông A tiếp tục gửi thêm một số tháng tròn nữa rồi rút cả vốn lẫn lãi được 10937826,46912 đồng (chưa làm tròn). Hỏi ông A đã gửi tổng là bao nhiêu tháng? ( Biết rằng kỳ hạn là một tháng, lãi suất nếu có thay đổi chỉ thay đổi sau khi hết tháng và trong quá trình gửi ông A không rút đồng nào, tiền lãi của mỗi tháng được cộng vào tiền gốc của tháng sau).

A. 12 tháng
B. 13 tháng
C. 9 tháng
D. 10 tháng
Câu 152 : Cho $a, b > 0; m, n \in ℤ *$ . Trong các đẳng thức sau, đẳng thức nào sai?

A. $\sqrt[m]{a} : \sqrt[m]{b} = \sqrt[m]{a : b}$
B. ${(\sqrt[m]{a})}^{n} = \sqrt[m]{a^{n}}$
C. $\sqrt[m]{a} . \sqrt[m]{b} = \sqrt[m]{a b}$
D. $\sqrt[m]{a} + \sqrt[m]{b} = \sqrt[m]{a + b}$
Câu 153 : Một khối đá có hình một khối cầu có bán kính R, người thợ thủ công mỹ nghệ cần cắt và gọt viên đá đó thành một viên đá cảnh có hình dạng là một khối trụ. Tính thể tích lớn nhất có thể của viên đá cảnh sau khi đã hoàn thiện.

A. $\frac{4 \sqrt{3} {πR}^{3}}{3}$
B. $\frac{4 \sqrt{3} {πR}^{3}}{9}$
C. $\frac{4 \sqrt{3} {πR}^{3}}{6}$
D. $\frac{4 \sqrt{3} {πR}^{3}}{12}$

Câu 154 : Trong mặt phẳng tọa độ Oxy, cho biết A(3;5). Tìm tọa độ A’ là ảnh của điểm A qua phép đối xứng trục Ox.

A. A'(-3;-5)
B. A'(5;3)
C. A'(-3;5)
D. A'(3;-5)
Câu 155 : Cho $0 < a \neq 1$ . Trong các đẳng thức sau, đẳng thức nào đúng?

A. $\log_{\sqrt[3]{a}} (a \sqrt[3]{a^{2}}) = - 3$
B. $\log_{\sqrt[3]{a}} (a \sqrt[3]{a^{2}}) = 5$
C. $\log_{\sqrt[3]{a}} (a \sqrt[3]{a^{2}}) = 2$
D. $\log_{\sqrt[3]{a}} (a \sqrt[3]{a^{2}}) = 3$
Câu 156 : Cho đường thẳng a và mặt phẳng (P) đường thẳng b đối xứng với đường thẳng a qua mặt phẳng (P). Khi nào thì $b ⊥ a$ ?

A. $K h i a \subset (P)$
B. $K h i (a, (P)) = 90 °$
C. $K h i (a, (P)) = 45 °$
D. $K h i a / / (P)$
Câu 157 : Trong không gian với hệ tọa độ Oxyz cho M(2;3;-2), N(-2;-1;4). Tìm tọa độ điểm E thuộc trục cao sao cho tam giác MNE cân tại E.

A. $(0; 0; \frac{1}{2})$
B. $(0; 0; \frac{- 1}{3})$
C. $(0; 0; \frac{1}{3})$
D. $(0; 0; \frac{- 1}{2})$

Câu 158 : Cho hàm số $y = x^{3} - 3 x + 2$ . Tọa độ điểm cực tiểu của đồ thị hàm số là

A. (-2;0)
B. (-1;4)
C. (0;1)
D. (1;0)
Câu 159 : Cho hàm số f(x) có đồ thị f ' (x) của nó

A. 1
B. 4
C. 3
D. 2
Câu 160 : Đồ thị hàm số $y = \frac{\sqrt{4 - x^{2}}}{x^{2} - 3 x - 4}$ có tất cả bao nhiêu đường tiệm cận.

A. 3
B. 0
C. 2
D. 1
Câu 161 : Tìm tọa độ điểm biểu diễn số phức $z = \frac{(2 - 3 i) (4 - i)}{3 + 2 i}$ ?

A. (-1;-4)
B. (1;4)
C. (1;-4)
D. (-1;4)

Câu 162 : Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình sinx = 0?

A. cosx = -1
B. cosx = 1
C. tanx = 0
D. cotx = 1
Câu 163 : Tìm hàm số F(x) biết F(x) là một nguyên hàm của hàm số $f (x) = \sqrt{x}$ và $F (1) = 1$

A. $F (x) = \frac{2}{3} x \sqrt{x}$
B. $F (x) = \frac{2}{3} x \sqrt{x} + \frac{1}{3}$
C. $F (x) = \frac{1}{2 \sqrt{x}} + \frac{1}{2}$
D. $F (x) = \frac{2}{3} x \sqrt{x} - \frac{5}{3}$
Câu 164 : Đồ thị hai hàm số $y = \frac{2 x^{2} - x + 1}{x - 1}$ và y = x - 1 cắt nhau tại hai điểm A, B. Tính độ dài đoạn thẳng AB

A. AB = 2
B. $A B = \sqrt{2}$
C. $A B = \sqrt{10}$
D. $A B = \frac{1}{\sqrt{2}}$
Câu 165 : Tìm toạ độ giao điểm I của hai đường tiệm cận của đồ thị hàm số $y = \frac{2 x - 1}{2 - 3 x}$

A. $I (\frac{2}{3}; 1)$
B. $I (\frac{2}{3}; - \frac{2}{3})$
C. $I (\frac{3}{2}; - \frac{2}{3})$
D. $I (- \frac{2}{3}; \frac{2}{3})$

Câu 166 : Tìm tập xác định của hàm số $y = \frac{1}{\sin x} - \frac{1}{\cos x}$ .

A. $ℝ \ \{\frac{k π}{2}, k \in ℤ\}$
B. $ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$
C. $ℝ \ \{k π, k \in ℤ\}$
D. $ℝ \ \{k 2 π, k \in ℤ\}$
Câu 167 : Cho 6 chữ số 2;3;4;5;6;7. Từ các chữ số trên có thể lập được bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau?

A. 120
B. 60
C. 20
D. 40
Câu 168 : Giải phương trình $\sqrt{3} t a n x + 3 = 0$

A. $x = - \frac{π}{3} + k π, k \in ℤ$
B. $x = \frac{π}{6} + k π, k \in ℤ$
C. $x = - \frac{π}{6} + k π, k \in ℤ$
D. $x = \frac{π}{3} + k π, k \in ℤ$
Câu 169 : Cho tứ diện ABCD, G là trọng tâm $∆ A B D$ và M là điểm trên cạnh BC sao cho BM = 2MC. Đường thẳng MG song song với mặt phẳng nào sau đây:

A. (ABC)
B. (ABD)
C. (BCD)
D. (ACD)

Câu 170 : Tìm hệ số của $x^{97}$ trong khai triển đa thức ${(x - 2)}^{100}$ .

A. 1293600
B. -1293600
C. ${(- 2)}^{97} C_{100}^{97}$
D. $2^{97} C_{100}^{97}$
Câu 171 : Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình dưới đây : $\log (x - 40) + \log (60 - x) < 2 ?$

A. 20
B. 10
C. Vô số
D. 18
Câu 172 : Trong các bất đẳng thức sau, bất đẳng thức nào sai?

A. $\log_{2} 5 > \log_{2} π$
B. $\log_{\sqrt{2} - 1} π > \log_{\sqrt{2} - 1} e$
C. $\log_{\sqrt{3} + 1} π < \log_{\sqrt{3} + 1} 7 .$
D. $\log_{7} 5 < 1$
Câu 173 : Cho đường thẳng d song song mặt phẳng ( $α$ ) nằm trong mặt phẳng ( $β$ ). Gọi a là giao tuyến của ( $α$ ) và ( $β$ ). Khi đó

A. a và d trùng nhau
B. a và d cắt nhau
C. a song song d
D. a và d chéo nhau

Câu 174 : Tính bán kính mặt cầu ngoại tiếp khối chóp tứ giác đều có cạnh đáy bằng 1 và góc giữa cạnh bên và mặt đáy bằng $60 °$ .

A. $\frac{\sqrt{6}}{4}$
B. $\frac{\sqrt{6}}{2}$
C. $\frac{\sqrt{6}}{3}$
D. $\frac{\sqrt{6}}{6}$
Câu 175 : Kí hiệu M là giá trị lớn nhất của hàm số $y = \sin 2 x - \cos 2 x$ . Tìm M ?

A. M = $2 \sqrt{2}$
B. M = 1
C. M = 2
D. M = $\sqrt{2}$
Câu 176 : Cho hai số thực dương a, b thỏa mãn $\log_{a} b = 2$ . Tính $\log_{\frac{\sqrt{a}}{b}} (\sqrt[3]{b} . a)$

A. $- \frac{10}{9}$
B. $\frac{2}{3}$
C. $- \frac{2}{9}$
D. $\frac{2}{15}$
Câu 177 : Cho biết $C_{n}^{6} = 6$ . Tìm số hạng không chứa x trong khai triển của ${(x - \frac{1}{x})}^{n} .$

A. 9
B. 6
C. 8
D. Cả ba phương án trên đều sai

Câu 178 : Cho khối lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình vuông. Hình chiếu vuông góc của A' trên mặt phẳng (ABCD) là trung điểm của AB, góc giữa mặt phẳng (A'CD) và mặt phẳng (ABCD) là $60 °$ . Thể tích của khối chóp B'ABCD là $\frac{8 \sqrt{3} a^{3}}{3}$ . Tính độ dài đoạn thẳng AC.

A. $\frac{2 a}{\sqrt[3]{3}}$
B. $\frac{2 \sqrt{2} a}{\sqrt[3]{3}}$
C. $2 a$
D. $2 \sqrt{2} a$
Câu 179 : Cho biết tập xác định của hàm số $y = \log_{\frac{1}{2}} (- 1 + \log_{\frac{1}{4}} x)$ là một khoảng có độ dài $\frac{m}{n}$ (phân số tối giản). Tính giá trị m + n.

A. 6
B. 5
C. 4
D. 7
Câu 180 : Cho khai triển ${(2 x - 1)}^{20} = a_{0} + a_{1} x + a_{2} x^{2} + . . . + a_{20} x^{20}$ . Tính $a_{3}$ ?

A. $a_{3} = 9120$
B. $a_{3} = - 9120$
C. $a_{3} = - 1140$
D. $a_{3} = 1140$
Câu 181 : Tính tích tất cả các nghiệm của phương trình ${(\log_{2} (4 x))}^{2} + \log_{2} (\frac{x^{2}}{8}) = 8$ .

A. $\frac{1}{32}$
B. $\frac{1}{6}$
C. $\frac{1}{64}$
D. $\frac{1}{128}$

Câu 182 : Trong không gian với hệ tọa độ Oxyz cho $\vec{u} = (- 2; 3; 0); \vec{v} = (2; - 2; 1)$ , tọa độ của véc tơ $\vec{w} = \vec{u} - 2 \vec{v}$ là

A. (-6;7;-2)
B. (6;-8;1)
C. (6;3;0)
D. (-6;3;0)
Câu 183 : Trong không gian với hệ tọa độ Oxyz cho $\vec{u} = (- 2; 3; 0), \vec{v} = (2; - 2; 1)$ , độ dài của véc tơ $\vec{w} = \vec{u} + 2 \vec{v}$ là

A. 3
B. 5
C. 2
D. 9
Câu 184 : Tìm tất cả các giá trị của tham số m để đồ thị hàm số $y = x^{4} - 2 m^{2} x^{2} + 2 m$ có ba điểm cực trị A, B, C sao cho O, A, B, C là các đỉnh của một hình thoi (với O là gốc tọa độ).

A. m = 3
B. m = 1
C. m = -1
D. m = 2
Câu 185 : Lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông cân tại A, BC = 2a , cạnh bên AA' = 3a và có hai đáy là hai tam giác nội tiếp hai đường tròn đáy của hình trụ $(τ)$ . Tính thể tích khối trụ $(τ)$ .

A. $π a^{3}$
B. $3 π a^{3}$
C. $3 \sqrt{3} π a^{3}$
D. $4 π a^{3}$

Câu 186 : Trong không gian với hệ tọa độ Oxyz, cho ba vec tơ $\vec{a} (1; m; 2); \vec{b} (m + 1; 2; 1); \vec{c} (0; m - 2; 2) .$ Giá trị của m để $\vec{a}, \vec{b}, \vec{c}$ đồng phẳng là:

A. $\frac{2}{5}$
B. $- \frac{2}{5}$
C. $\frac{1}{5}$
D. 1
Câu 187 : Trong hệ trục tọa độ Oxy, cho hai đường tròn (C) và (C') lần lượt có phương trình là ${(x - 1)}^{2} + {(y + 2)}^{2} = 4$ và ${(x + 2)}^{2} + {(y - 1)}^{2} = 4$ . Xét phép tịnh tiến theo vectơ $\vec{v}$ biến đường tròn (C) thành đường tròn (C').Tìm $\vec{v}$ ?

A. $\vec{v} = (- 3; 3)$
B. $\vec{v} = (- 1; - 1)$
C. $\vec{v} = (3; - 3)$
D. $\vec{v} = (1; 1)$
Câu 188 : Cho cấp số nhân $(u_{n})$ , biết $u_{1} = 2; u_{4} = 54 .$ Tính $S_{10}$ là tổng của 10 số hạng đầu tiên trong cấp số nhân đã cho?

A. $S_{10} = 118096$
B. $S_{10} = 59048$
C. $S_{10} = - 59048$
D. $S_{10} = 29524$
Câu 189 : Tìm nghiệm dương nhỏ nhất thỏa mãn phương trình $\sin 2 x - \cos 2 x + \sin x - \cos x = 1$ ?

A. $x = \frac{π}{4}$
B. $x = \frac{5 π}{4}$
C. $x = \frac{2 π}{3}$
D. $x = \frac{π}{6}$

Câu 190 : Hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, $S A ⊥ (A B C D)$ , SC tạovới mặt đáy một góc $45 °$ . Mặt cầu ngoại tiếp hình chóp S.ABCD có bán kính bằng $a \sqrt{2}$ . Thể tích khối chóp S.ABCD bằng:

A. $2 a^{3}$
B. $2 a^{3} \sqrt{3}$
C. $\frac{a^{3} \sqrt{3}}{3}$
D. $\frac{2 a^{3} \sqrt{3}}{3}$
Câu 191 : Đạo hàm của hàm số $y = (x + 2) e^{2 x}$ là

A. $y' = (2 x - 4) e^{x}$
B. $y' = (2 x + 5) e^{2 x}$
C. $y' = (2 x + 5) e^{x}$
D. $y' = (2 x + 4) e^{2 x}$
Câu 192 : Hình nón có đáy là hình tròn bán kính R, chiều cao h . Kết luận nào sau đây sai ?

A. Góc ở đỉnh là $α = 2 a r c \tan \frac{R}{h}$
B. Đường sinh hình nón $l = \sqrt{h^{2} + R^{2}}$
C. Diện tích xung quanh $S_{x q} = πR \sqrt{R^{2} + h^{2}}$
D. Thể tích khối nón $V = {πR}^{2} h .$
Câu 193 : Cho a là một số thực dương khác 1 thoả mãn $\log_{4} \sqrt{a} = 5$ . Tính $\log_{a} 2$

A. $\log_{a} 2 = \frac{1}{5}$
B. $\log_{a} 2 = 5$
C. $\log_{a} 2 = 20$
D. $\log_{a} 2 = \frac{1}{20}$

Câu 194 : Cho hàm số y = f(x) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

A. Hàm số có giá trị cực tiểu bằng 2
B. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -2
C. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 2
D. Hàm số có ba cực trị
Câu 195 : Cho hình chóp S.ABC đáy là tam giác ABC có diện tích bằng 2, cạnh bên SA vuông góc với mặt phẳng đáy, SA = 4. Thể tích của khối chóp S.ABC là

A. 8
B. $\frac{1}{2}$
C. $\frac{16}{3}$
D. $\frac{8}{3}$
Câu 196 : Trong không gian với hệ tọa độ Oxyz, cho hai véctơ $\vec{a} = (2; - 3; 1)$ và $\vec{b} = (- 1; 0; 4)$ . Tìm tọa độ véctơ $\vec{u} = - 2 \vec{a} + 3 \vec{b}$ .

A. $\vec{u} = (- 7; - 6; 10)$
B. $\vec{u} = (- 7; 6; 10)$
C. $\vec{u} = (7; 6; 10)$
D. $\vec{u} = (- 7; 6; - 10)$
Câu 197 : Tìm số nghiệm thuộc khoảng $(- π; π)$ của phương trình cosx + sin2x = 0

A. 4
B. 3
C. 1
D. 2

Câu 198 : Cho hình chóp S.ABCD có đáy là hình chữ nhật AB = a, AC = $a \sqrt{5}$ . Cạnh bên SA = $a \sqrt{3}$ và vuông góc với (ABCD). Tính theo a thể tích của khối chóp S.ABC

A. $\frac{2 \sqrt{3} a^{3}}{3}$
B. $\frac{\sqrt{15} a^{3}}{6}$
C. $\frac{\sqrt{3} a^{3}}{2}$
D. $\frac{\sqrt{3} a^{3}}{3}$
Câu 199 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA = $a \sqrt{2}$ . Tìm số đo của góc giữa đường thẳng SC và mặt phẳng (SAB)

A. 30 $°$
B. 90 $°$
C. 45 $°$
D. 60 $°$
Câu 200 : Trong không gian với hệ tọa độ Oxyz, mặt cầu $x^{2} + y^{2} + z^{2} - 2 x - 4 y + 6 z - 2 = 0$ cắt mặt phẳng Oxy theo giao tuyến là một đường tròn. Tìm tâm và bán kính của đường tròn này

A. $I (1; - 2; 0), r = \sqrt{5}$
B. $I (1; 2; 0), r = 2 \sqrt{5}$
C. $I (1; 2; 0), r = \sqrt{7}$
D. $I (- 1; - 2; 0), r = 2 \sqrt{7}$
Câu 201 : Tìm hệ số của số hạng chứa $x^{5}$ trong khai triển ${(x^{2} + \frac{2}{x})}^{7}$

A. 560
B. 35
C. 280
D. 84

Câu 202 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA = 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)?

A. $\frac{\sqrt{5}}{5}$
B. $\frac{2 \sqrt{5}}{5}$
C. $\frac{1}{2}$
D. 1
Câu 203 : Tìm tất cả các giá trị của tham số m để hàm số $y = \frac{m x - 2}{m - 2 x}$ nghịch biến trên $(\frac{1}{2}; + \infty)$

A. $- 2 < m \leq 1$
B. m > 2
C. -2 < m < 2
D. $- 2 \leq m \leq 2$
Câu 204 : Cho f(x), g(x) là các hàm số xác định và liên tục trên $ℝ$ . Trong các mệnh đề sau, mệnh đề nào sai?

A. $\int [2 f (x) + 3 g (x)] d x = 2 \int f (x) d x + 3 \int g (x) d x$
B. $\int [f (x) - g (x)] d x = \int f (x) d x - \int g (x) d x$
C. $\int 2 f (x) d x = 2 \int f (x) d x$
D. $\int f (x) . g (x) d x = \int f (x) d x . \int g (x) d x$
Câu 205 : Cho số phức z thỏa mãn điều kiện (1 - i)(2 + i)z + 1 - i = (5 - i)(1 + i). Tính môđun của số phức $w = 1 + 2 z + z^{2}$

A. 8
B. 64
C. $2 \sqrt{2}$
D. $\sqrt{5}$

Câu 206 : Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và OA = OB = OC = a (tham khảo hình vẽ). 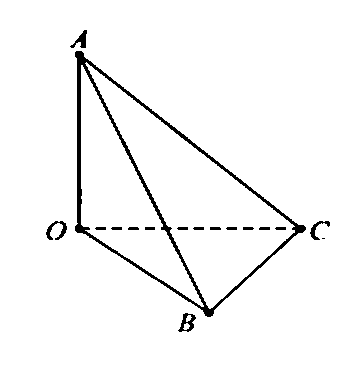Tính khoảng cách giữa hai đường thẳng AB và OC

A. $\frac{a}{2}$
B. $\frac{a \sqrt{2}}{2}$
C. $\frac{a \sqrt{3}}{2}$
D. $\frac{3 a}{4}$
Câu 207 : Cho hàm số $y = \frac{x + 2}{x + 1} (C)$ . Gọi d là khoảng cách từ giao điểm hai tiệm cận của đồ thị (C) đến một tiếp tuyến của (C). Giá trị lớn nhất d có thể đạt được là:

A. $3 \sqrt{3}$
B. $\sqrt{3}$
C. $\sqrt{2}$
D. $2 \sqrt{2}$
Câu 208 : Hàm f(x) có đạo hàm $f' (x) = x^{2} (x + 2)$ . Phát biểu nào sau đây là đúng?

A. Hàm số nghịch biến trên các $(- \infty; - 2)$ và $(0; + \infty)$
B. Hàm số đồng biến trên các khoảng $(- \infty; - 2)$ và $(0; + \infty)$
C. Hàm số đồng biến trên khoảng $(- 2; + \infty)$
D. Hàm số nghịch biến trên khoảng $(- 2; 0)$
Câu 209 : Đặt $I = \lim_{x \to 0} \frac{x \log_{a} (1 - 2 x) + 1 - \cos x}{x^{2}}, 0 < a \neq 1$ cho trước. Kết quả nào sau đây đúng?

A. $I = \frac{1}{2} - \frac{2}{\ln a}$
B. $I = \ln a - \frac{1}{2}$
C. $I = \frac{1}{2} + \frac{2}{\ln a}$
D. $I = \ln a + \frac{1}{2}$

Câu 210 : Trong không gian với hệ trục tọa độ Oxyz, cho điểm M thỏa mãn OM = 7. Biết rằng khoảng cách từ M đến (Oxz), (Oyz) lần lượt là 2 và 3. Tính khoảng cách từ M đến (Oxy).

A. 12
B. 5
C. 2
D. 6
Câu 211 : Tính môđun của số phức z thỏa mãn $3 z . \bar{z} + 2017 (z - \bar{z}) = 48 - 2016 i$

A. $|z| = 4$
B. $|z| = \sqrt{2016}$
C. $|z| = \sqrt{2017}$
D. $|z| = 2$
Câu 212 : Cho hàm số f(x) liên tục trên [0;1] thỏa mãn $f (x) = 6 x^{2} . f (x^{3}) - \frac{6}{\sqrt{3 x + 1}}$ . Tính $\int_{0}^{1} f (x) d x$ .

A. 2
B. 4
C. -1
D. 6
Câu 213 : Người ta muốn xây một bể nước dạng hình hộp chữ nhật không nắp có thể tích bằng $\frac{500}{3} m^{3}$ đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê công nhân xây bể là 500000đồng/ $m^{2}$ . Chi phí công nhân thấp nhất là:

A. 150 triệu đồng
B. 75 triệu đồng
C. 60 triệu đồng
D. 100 triệu đồng

Câu 214 : Một công ty dự kiến làm một đường ống thoát nước thải hình trụ dài 1km, đường kính trong ống (không kể lớp bê tông) bằng 1m; độ dày của lớp bê tông bằng 10cm. Biết rằng cứ một khối bê tông phải dùng 10 bao xi măng. Số bao xi măng công ty phải dùng để xây dựng đường ông thoát nước gần đúng với số nào nhất?

A. 3456 bao
B. 3450 bao
C. 4000 bao
D. 3000 bao
Câu 215 : Cho hình chóp S.ABCD có đáy là hình vuông tâm O, SA vuông góc với đáy ABCD. Gọi I là trung điểm của SC. Xét các khẳng định sau:

A. 3
B. 1
C. 4
D. 2
Câu 216 : Cho đa thức $P (x) = {(2 x - 1)}^{1000}$ . Khai triển và rút gọn ta được

A. $a_{1000} + a_{999} + . . . + a_{1} = 0$
B. $a_{1000} + a_{999} + . . . + a_{1} = 2^{1000} - 1$
C. $a_{1000} + a_{999} + . . . + a_{1} = 1$
D. $a_{1000} + a_{999} + . . . + a_{1} = 2^{1000}$
Câu 217 : Cho tam giác ABC có BAC = 120 $°$ , AB = AC = a . Quay tam giác ABC (bao gồm cả điểm trong tam giác) quanh đường thẳng AB ta được một khối tròn xoay. Thể tích khối tròn xoay đó bằng :

A. $\frac{{πa}^{3}}{3}$
B. $\frac{{πa}^{3}}{4}$
C. $\frac{{πa}^{3} \sqrt{3}}{2}$
D. $\frac{{πa}^{3} \sqrt{3}}{4}$

Câu 218 : Cho hàm số $y = \frac{x + b}{a x - 2} (a b \neq - 2)$ . Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-2) song song với đường thẳng $d : 3 x + y - 4 = 0$ . Khi đó giá trị của a - 3b bằng

A. -2
B. 4
C. -1
D. 5
Câu 219 : Trong các khối trụ có cùng diện tích toàn phần bằng $π$ . Gọi $(τ)$ là khối trụ có thể tích lớn nhất, chiều cao của $(τ)$ bằng

A. $\frac{π}{3}$
B. $\frac{\sqrt{6}}{3}$
C. $\frac{\sqrt{6}}{6}$
D. $\frac{π \sqrt{3}}{4}$
Câu 220 : Gọi S là tổng các nghiệm của phương trình $\frac{\sin x}{\cos x + 1} = 0$ trên đoạn [0;2017 $π$ ] .Tính S.

A. $S = 2035153 π$
B. $S = 1001000 π$
C. $S = 1017072 π$
D. $S = 200200 π$
Câu 221 : Cho hình chóp S.ABC có SA $⊥$ (ABC) và góc BAC=120 $°$ . Hình chiếu của A trên các đoạn SB, SC lần lượt là M, N. Tính góc giữa hai mặt phẳng (ABC) và (AMN)

A. $45 °$
B. 60 $°$
C. 15 $°$
D. 30 $°$

Câu 222 : Ký hiệu $f (x) - {(x^{1 + \frac{1}{2 \log_{4} x}} + 8^{\frac{1}{3 \log_{x^{2}} 2}} + 1)}^{\frac{1}{2}} - 1 .$ Giá trị của $f (f (2017))$ bằng:

A. 1500
B. 2017
C. 1017
D. 2000
Câu 223 : Gọi M là điểm có hoành độ khác 0, thuộc đồ thị (C) của hàm số $y = x^{3} - 3 x$ . Tiếp tuyến của (C) tại M cắt (C) tại điểm thứ hai là N (N không trùng với M). Kí hiệu $x_{M}, x_{N}$ thứ tự là hoành độ của M và N. Kết luận nào sau đây là đúng?

A. $2 x_{M} + x_{N} = 0$
B. $x_{M} + 2 x_{N} = 3$
C. $x_{M} + x_{N} = - 2$
D. $x_{M} + x_{N} = 3$
Câu 224 : Cho dãy số $(u_{n})$ xác định bởi $u_{1} = 1$ và $u_{n + 1} = \sqrt{u_{n}^{2} + 2}, \forall n \in N *$ . Tổng $S = u_{1}^{2} + u_{2}^{2} + u_{3}^{2} + . . . + u_{1001}^{2}$ bằng

A. 1002001
B. 1001001
C. 1001002
D. 1002002
Câu 225 : Cho một tấm nhôm hình chữ nhật ABCD có AD = 60 cm. Ta gập tấm nhôm theo hai cạnh MN và PQ vào phía trong đến khi AB và DC trùng nhau, với AN = PD (như hình vẽ dưới đây) để được một hình lăng trụ. Tìm độ dài đoạn AN để thể tích khối lăng trụ lớn nhất.

A. AN = 39 cm
B. AN = 20 cm
C. AN = $\frac{15}{2}$ cm
D. AN = 15 cm

Câu 226 : Một công ty điện lực bán điện sinh hoạt cho dân theo hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 10 số; bậc 1 từ số thứ 1 đến số thứ 10, bậc 2 từ số thứ 11 đến số thứ 20, bậc 3 từ số thứ 21 đến số thứ 30,.... Bậc 1 có giá là 500 đồng/1số, giá của mỗi số ở bậc thứ n +1 tăng so với giá của mỗi số ở bậc thứ n là $2, 5 %$ . Gia đình ông A sử dụng hết 847 số trong tháng 1, hỏi tháng 1 ông A phải đóng bao nhiêu tiền? (Kết quả làm tròn đến hàng phần trăm)

A. $x \approx 1431392, 85$
B. $x \approx 1419455, 83$
C. $x \approx 1914455, 82$
D. $x \approx 1542672, 87$
Câu 227 : Cho hàm số $f (x) = x^{3} - 3 x^{2} + 4$ . Tính $f' (1)$ .

A. -3
B. 0
C. 9
D. 3
Câu 228 : Trong các dãy số sau, dãy số nào không là cấp số cộng?

A. $\frac{1}{2}; \frac{1}{4}; \frac{1}{6}; \frac{1}{8}; \frac{1}{10}$
B. $\frac{1}{2}; \frac{3}{2}; \frac{5}{2}; \frac{7}{2}; \frac{9}{2}$
C. -8;-6;-4;-2;0
D. 2;2;2;2;2
Câu 229 : Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy ABC là tam giác cân tại C. Gọi H và K lần lượt là trung điểm của AB và SB. Trong các khẳng định sau, khẳng định nào sai?

A. $C H ⊥ S B$
B. $A K ⊥ B C$
C. $C H ⊥ S A$
D. $C H ⊥ A K$

Câu 230 : Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-1;2;4) và B(0;1;5). Gọi (P) là mặt phẳng đi qua A sao cho khoảng cách từ B đến (P) là lớn nhất. Khi đó, khoảng cách d từ O đến mặt phẳng (P) bằng bao nhiêu?

A. $d = - \frac{\sqrt{3}}{3}$
B. $d = \sqrt{3}$
C. $d = \frac{1}{3}$
D. $d = \frac{1}{\sqrt{3}}$
Câu 231 : Hỏi khối đa diện đều loại {4;3} có bao nhiêu mặt?

A. 4
B. 20
C. 6
D. 12
Câu 232 : Giải phương trình $\cos 2 x + 5 \sin x - 4 = 0 .$

A. $x = \frac{π}{2} + k π$
B. $x = - \frac{π}{2} + k π$
C. $x = k 2 π$
D. $x = \frac{π}{2} + k 2 π$
Câu 233 : Cho hàm số $\frac{3 x - 1}{- 2 + x}$ . Khẳng định nào sau đây là đúng?

A. Hàm số luôn nghịch biến trên $ℝ$
B. Hàm số luôn nghịch biến trên từng khoảng xác định
C. Hàm số đồng biến trên các khoảng $(- \infty; 2) v à (2; + \infty)$
D. Hàm số luôn nghịch biến các khoảng $(- \infty; - 2) v à (- 2; + \infty)$

Câu 234 : Số các giá trị nguyên dương của tham số m để hàm số $y = {(\frac{1}{2})}^{x^{3} - 6 x^{2} + m x + 2}$ luôn đồng biến trên khoảng (1;3) là

A. 8
B. 9
C. 10
D. Vô số.
Câu 235 : Tìm giá trị của tham số m để hàm số $f (x) = \{\begin{cases} \frac{\sqrt{3 x + 1} - 2}{x - 1} k h i x \neq 1 \\ m k h i x = 1 \end{cases}$ liên lục tại điểm $x_{0} = 1$

A. m = 3
B. m = 1
C. m = $\frac{3}{4}$
D. m = $\frac{1}{2}$
Câu 236 : Biết nghiệm của phương $2^{x} . 15^{x + 1} = 3^{x + 3}$ được viết dưới dạng x = 2loga - logb là các số nguyên dương nhỏ hơn 10. Tính S = $2017 a^{3} - 2018 b^{2}$

A. S = 4009
B. S = 2014982
C. S =1419943
D. S = -197791
Câu 237 : Cho hàm số $y = x^{3} - m x^{2} - m x + 2 m - 3$ có đồ thị là (C), với m là tham số thực. Gọi T là tập tất cả giá trị nguyên của m để mọi đường thẳng tiếp xúc với (C) đều có hệ số góc dương. Tính tổng các phần tử của T.

A. 3
B. 6
C. -6
D. -3

Câu 238 : Tìm tổng tất cả các nghiệm thuộc đoạn $[0; 10 π]$ của phương trình $\sin^{2} 2 x + 3 \sin 2 x + 2 = 0$ ?

A. $\frac{105}{2} π$
B. $\frac{105}{4} π$
C. $\frac{297}{4} π$
D. $\frac{299}{4} π$
Câu 239 : Cho tam giác SOA vuông tại O có MN//SO với M, N lần lượt nằm trên cạnh SA, OA như hình vẽ bên. Đặt SO = h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O bán kính R = OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất

A. $M N = \frac{h}{2}$
B. $M N = \frac{h}{3}$
C. $M N = \frac{h}{4}$
D. $M N = \frac{h}{6}$
Câu 240 : Với n là số nguyên dương thỏa mãn đăng thức $3 C_{n + 1}^{3} - 3 A_{n}^{2} = 52 (n - 1)$ . Trong khai triển biểu thức ${(x^{3} + 2 y^{2})}^{n}$ , gọi $T_{k}$ là số hạng mà tổng số mũ của x và y của số hạng đó bằng 34. Hệ số của là

A. 54912
B. 1287
C. 2574
D. 41184
Câu 241 : Cho phương trình $25^{x} - (m + 2) 5^{x} + 2 m + 1 = 0$ với m là số thực. Có bao nhiêu giá trị nguyên $m \in [0; 2018]$ để phương trình có nghiệm?

A. 2015
B. 2016
C. 2018
D. 2017

Câu 242 : Hàm số $y = \ln (x + 2) + \frac{3}{x + 2}$ đồng biến trên khoảng nào sau đây?

A. $(- \infty; 1)$
B. $(1; + \infty)$
C. $(\frac{1}{2}; 1)$
D. $(- \frac{1}{2}; + \infty)$
Câu 243 : Tìm số đường tiệm cận của đồ thị hàm số $y = \frac{2 x - \sqrt{x^{2} - x - 6}}{x^{2} - 1}$

A. 1
B. 2
C. 3
D. 4
Câu 244 : Phương trình tiếp tuyến của đồ thị hàm số $y = x^{3} - 3 x^{2} + 1$ tại điểm A(3;1)?

A. -9x - 26
B. 9x - 26
C. -9x - 3
D. 9x - 2
Câu 245 : Cho hàm số $y = - 2017 e^{- x} - 3 e^{- 2 x} .$ Mệnh đề nào dưới đây đúng?

A. $y'' + 3 y' + 2 y = - 2017$
B. $y'' + 3 y' + 2 y = - 3$
C. $y'' + 3 y' + 2 y = 0$
D. $y'' + 3 y' + 2 y = 2$

Câu 246 : Tìm số giao điểm của đồ thị (C): $y = x^{3} - 3 x^{2} + 2 x + 2017$ và đường thẳng y = 2017.

A. 3
B. 0
C. 1
D. 2
Câu 247 : Tiếp tuyến với đồ thị hàm số $y = \frac{2 x + 1}{x + 1}$ tại điểm có hoành độ bằng 0 cắt hai trục tọa độ lần lượt tại A và B. Diện tích tam giác OAB bằng

A. 2
B. 3
C. $\frac{1}{2}$
D. $\frac{1}{4}$
Câu 248 : Cho hàm số y = ln x. Khẳng định nào sau đây là khẳng định sai?

A. Hàm số đồng biến trên khoảng $(0; + \infty)$
B. Hàm số có tập giá trị là $(- \infty; + \infty)$
C. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng
D. Hàm số có tập giá trị là $(0; + \infty)$
Câu 249 : Tính đạo hàm của hàm số $y = \log_{2} (2 x + 1)$ .

A. $y' = \frac{2}{2 x + 1}$
B. $y' = \frac{2}{(2 x + 1) \ln 2}$
C. $y' = \frac{1}{(2 x + 1) \ln 2}$
D. $y' = \frac{1}{2 x + 1}$

Câu 250 : Tìm tập xác định D của hàm số $y = {(2 - x)}^{1 - \sqrt{3}}$ .

A. $D = (- \infty; + \infty)$
B. $D = (- \infty; 2]$
C. $D = (- \infty; 2)$
D. $D = (2; + \infty)$
Câu 251 : Cho a > 0, a $\neq$ 1,x,y là hai số thực khác 0. Khẳng định nào sau đây là khẳng định đúng?

A. $\log_{a} x^{2} = 2 \log_{a} x$
B. $\log_{a} (x y) = \log_{a} x + \log_{a} y$
C. $\log_{a} (x + y) = \log_{a} x + \log_{a} y$
D. $\log_{a} (x y) = \log_{a} |x| + \log_{a} |y|$
Câu 252 : Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau?

A. 648
B. 1000
C. 729
D. 720
Câu 253 : Một hộp có 5 bi đen, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất 2 bi được chọn có cùng màu là

A. $\frac{1}{4}$
B. $\frac{1}{9}$
C. $\frac{4}{9}$
D. $\frac{5}{9}$

Câu 254 : Trong khai triển đa thức $P (x) = {(x + \frac{2}{\sqrt{x}})}^{6} (x > 0) .$ Hệ số của $x^{3}$ là

A. 60
B. 80
C. 160
D. 240
Câu 255 : Tập xác định của hàm số $y = \ln (\frac{x}{\log_{2} x - 2})$ là

A. $D = (3; + \infty)$
B. $D = (- \infty; 0) \cup (3; + \infty)$
C. $D = (4; + \infty)$
D. $D = (- \infty; 0) \cup (4; + \infty)$
Câu 256 : Đường thẳng d: y = x - 5 cắt đồ thị (C): y = $\frac{x + 1}{x - 3}$ tại hai điểm A, B phân biệt. Gọi $d_{1}, d_{2}$ lần lượt là khoảng cách từ A và B đến đường thẳng $∆ : x = 0 .$ Tính $d = d_{1} + d_{2}$

A. d = 9
B. d = -1
C. d = 5
D. d = $5 \sqrt{2}$
Câu 257 : Một hộp chứa 12 viên bi kích thước khác nhau gồm 3 bi màu đỏ, 4 bi màu xanh và 5 bi màu vàng. Chọn ngẫu nhiên cùng một lúc 3 viên bi. Xác suất để 3 bi được chọn có đủ 3 màu là:

A. $\frac{3}{11}$
B. $\frac{3}{55}$
C. $\frac{3}{220}$
D. $\frac{1}{22}$

Câu 258 : Tìm giá trị của x,y sao cho dãy số -2 ,x ,6,y theo thứ tự lập thành một cấp số cộng?

A. x = -6, y = -2
B. x = 1, y = 7
C. x = 2, y = 8
D. x = 2, y = 10
Câu 259 : Trong các dãy số $(u_{n})$ được cho bởi các phương án dưới đây, dãy số nào là một cấp số cộng?

A. $u_{n} = \frac{2}{n}$
B. $u_{n} = n^{2}$
C. $u_{n} = n + 2$
D. $u_{n} = 2^{n}$
Câu 260 : Tính giới hạn $I = l i m (\sqrt{n^{2} - 2 n + 3} - n) ?$

A. I = -1
B. I = 0
C. I = $+ \infty$
D. I = 1
Câu 261 : Cho tứ diện ABCD. Khẳng định nào sau đây là đúng?

A. $\vec{A C} - \vec{C D} = \vec{A D}$
B. $\vec{A B} - \vec{A C} = \vec{D C} - \vec{D B}$
C. $\vec{A B} + \vec{C D} = \vec{A D} + \vec{C B}$
D. $\vec{A B} + \vec{A D} = \vec{B D}$

Câu 262 : Cho hàm số $y = x^{3} - 6 x^{2} + 9 x - 2 (C)$ . Đường thẳng đi qua điểm A(-1;1) và vuông góc với đường thẳng đi qua hai điểm cực trị của (C) là:

A. $y = - \frac{1}{2} x + \frac{3}{2}$
B. $y = \frac{1}{2} x + \frac{3}{2}$
C. y = x + 3
D. x - 2y - 3 = 0
Câu 263 : Cho hàm số $f (x) = {(\frac{1}{2})}^{x} . 5^{x^{2}} .$ Khẳng định nào sau đây là đúng:

A. $f (x) > 1 \Leftrightarrow - x \ln 2 + x^{2} \ln 5 > 0$
B. $f (x) > 1 \Leftrightarrow x^{2} + x \log_{2} 5 > 0$
C. $f (x) > 1 \Leftrightarrow x - x^{2} \log_{2} 5 > 0$
D. $f (x) > 1 \Leftrightarrow x^{2} - x \log_{2} 5 > 0$
Câu 264 : Cho hai đường thẳng $d_{1}, d_{2}$ song song nhau. Trên $d_{1}$ có 6 điểm tô màu đỏ, trên $d_{2}$ có 4 điểm tô màu xanh. Chọn ngẫu nhiên 3 điểm bất kì trong các điểm trên. Tính xác suất để 3 điểm được chọn lập thành tam giác có 2 đỉnh tô màu đỏ.

A. $\frac{5}{8}$
B. $\frac{5}{32}$
C. $\frac{5}{9}$
D. $\frac{1}{2}$
Câu 265 : Trên đoạn $[- π; π]$ phương trình $4 \sin x - 3 = 0$ có tất cả bao nhiêu nghiệm?

A. 1
B. 0
C. 2
D. 4

Câu 266 : Gọi n là số nguyên dương sao cho $\frac{1}{\log_{3} x} + \frac{1}{\log_{3^{2}} x} + \frac{1}{\log_{3^{3}} x} + . . . + \frac{1}{\log_{3^{n}} x} = \frac{210}{\log_{3} x}$ đúng với mọi x dương. Tìm giá trị của biểu thức P = 2n + 3.

A. P = 32
B. P = 40
C. P = 43
D. P = 23
Câu 267 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều, SC = SD = $a \sqrt{3}$ . Tính thể tích V của khối chóp S.ABCD theo a

A. $V = \frac{a^{3} \sqrt{2}}{6}$
B. $V = \frac{a^{3}}{6}$
C. $V = a^{3} \sqrt{2}$
D. $V = \frac{a^{3} \sqrt{3}}{3}$
Câu 268 : Cho lăng trụ tam giácABC.A'B'C'. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AC, AA', A' C', BC. Khẳng định nào dưới đây là khẳng định đúng?

A. $(M N P) / / (B B' C' C)$
B. $(N Q P) / / (A C' B')$
C. $(M N Q) / / (A' B' C')$
D. $(M P Q) / / (A A' B' B)$
Câu 269 : Cho hàm số $y = m x^{3} - x^{2} - 2 x + 8 m$ có đồ thị $(C_{m})$ . Tìm tất cả các giá trị của tham số m để đồ thị cắt trục hoành tại ba điểm phân biệt.

A. $m \in (- \frac{1}{6}; \frac{1}{2})$
B. $m \in [- \frac{1}{6}; \frac{1}{2}]$
C. $m \in (- \frac{1}{6}; \frac{1}{2}) \ \{0\}$
D. $m \in (- \infty; \frac{1}{2}) \ \{0\}$

Câu 270 : Đợt xuất khẩu gạo của Tỉnh Đồng Tháp thường kéo dài 2 tháng (60 ngày). Người ta nhận thấy số lượng gạo xuất khẩu tính theo ngày thứ t được xác định bởi công thức $S (t) = \frac{2}{5} t^{3} - 63 t^{2} + 3240 t - 3100$ (tấn) với $(1 \leq t \leq 60)$ . Hỏi trong 60 ngày đó thì ngày thứ mấy có số lượng xuất khẩu cao nhất?

A. 60
B. 45
C. 30
D. 25
Câu 271 : Hỏi có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $y = \frac{x^{2} - 3 x + 2}{x^{2} - m x - m + 5}$ không có đường tiệm cận đứng?

A. 9
B. 10
C. 11
D. 8
Câu 272 : Tính tổng $S = 1 + 2^{2} \log_{\sqrt{2}} 2 + 3^{2} \log_{\sqrt[3]{2}} 2 + 4^{2} \log_{\sqrt[4]{2}} 2 + . . . + 2017^{2} \log_{\sqrt[2017]{2}} 2 .$

A. $S = 1008^{2} . 2017^{2}$
B. $S = 1007^{2} . 2017^{2}$
C. $S = 1009^{2} . 2017^{2}$
D. $S = 1010^{2} . 2017^{2}$
Câu 273 : Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác vuông tại A, AB = a, AC = $a \sqrt{2}$ . Biết góc giữa hai mặt phẳng (AB'C') và (ABC) bằng $60 °$ và hình chiếu của A lên (A'B'C') là trung điểm H của đoạn thẳng A'B'. Tính bán kính mặt cầu ngoại tiếp tứ diện A.HB'C' theo a

A. $\frac{a \sqrt{21}}{7}$
B. $\frac{3 a \sqrt{6}}{8}$
C. $\frac{a \sqrt{62}}{8}$
D. $\frac{2 a \sqrt{21}}{7}$

Câu 274 : Cho hai số thực dương a, b thỏa mãn $\frac{9 a^{3} + a}{b + 1} = \sqrt{3 b + 2}$ . Giá trị lớn nhất của biểu thức S = 6a - b là

A. $\frac{17}{12}$
B. $\frac{82}{3}$
C. $\frac{11}{3}$
D. $\frac{89}{12}$
Câu 275 : Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;0;0), N(1;1;1). Mặt phẳng (P) thay đổi qua M, N cắt các trục Ox, Oy lần lượt tại B(0;b;0), C(0;0;c) với b > 0,c > 0. Hệ thức nào dưới đây đúng?

A. $b c = 2 (b + c)$
B. $b c = \frac{1}{b} + \frac{1}{c}$
C. $b c = b + c$
D. $b c = b - c$
Câu 276 : Cho hình lăng trụ ABC.A’B’C’ có thể tích bằng $6 a^{3}$ . Các điểm M, N, P lần lượt thuộc các cạnh AC', BB', CC' sao cho $\frac{A M}{A A'} = \frac{1}{2}, \frac{B N}{B B'} = \frac{C P}{C C'} = \frac{2}{3}$ . Tính thể tích V¢ của khối đa diện ABC.MNP ?

A. $V' = \frac{11}{27} a^{3}$
B. $V' = \frac{9}{16} a^{3}$
C. $V' = \frac{11}{3} a^{3}$
D. $V' = \frac{11}{18} a^{3}$
Câu 277 : Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y = \frac{m}{3} x^{3} + 7 m x^{2} + 14 x - m + 2$ nghịch biến trên nửa khoảng $[1; + \infty)$ ?

A. $(- \infty; - \frac{14}{15})$
B. $(- \infty; - \frac{14}{15}]$
C. $[- 2; - \frac{14}{15}]$
D. $[- \frac{14}{15}; + \infty)$

Câu 278 : Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a; tam giác A’BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABC) M là trung điểm của cạnh CC’. Tính cosin góc $α$ là góc giữa hai đường thẳng AA’ và BM

A. $\cos α = \frac{2 \sqrt{22}}{11}$
B. $\cos α = \frac{\sqrt{11}}{11}$
C. $\cos α = \frac{\sqrt{33}}{11}$
D. $\cos α = \frac{\sqrt{22}}{11}$
Câu 279 : Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = - 1 + 2 \cos x [(2 - \sqrt{3}) \sin x + c o s x]$ trên $ℝ$ . Biểu thức M + N + 2 có giá trị bằng:

A. 0
B. $4 \sqrt{2 - \sqrt{3}}$
C. 2
D. $\sqrt{2 + \sqrt{3}} + 2$
Câu 280 : Xác định giá trị thực k để hàm số $f (x) = \{\begin{cases} \frac{x^{2016} + x - 2}{\sqrt{2018 x + 1} - \sqrt{x + 2018}}, x \neq 1 \\ k, x = 1 \end{cases}$ liên tục tại x = 1.

A. $k = 1$
B. $k = 2 \sqrt{2019}$
C. $k = \frac{2017 . \sqrt{2018}}{2}$
D. $\frac{20016}{2017} \sqrt{2019}$
Câu 281 : Cho hàm số y = f(x) có đồ thị của hàm số y = f '(x) được cho như hình bên và các mệnh đề sau:

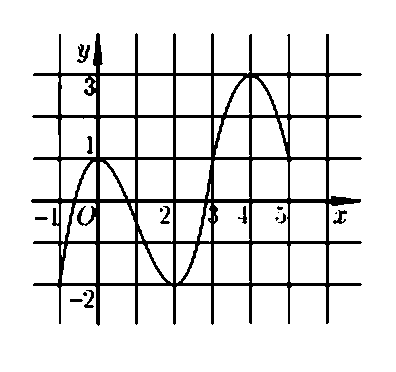
A. 1
B. 3
C. 4
D. 2

Câu 282 : Một bà mẹ Việt Nam anh hùng được hưởng số tiền là 4 triệu đồng trên một tháng (chuyển vào tài khoản ngân hàng của mẹ vào đầu tháng). Từ tháng 1 năm 2016 mẹ không đi rút tiền mà để lại ngân hàng và được tính lãi suất 1%trên một tháng. Đến đầu tháng 12 năm 2016 mẹ rút toàn bộ số tiền (bao gồm số tiền của tháng 12 và số tiền đã gửi từ tháng 1). Hỏi khi đó mẹ lĩnh về bao nhiêu tiền? (Kết quả làm tròn theo đơn vị nghìn đồng)

A. 50 triệu 730 nghìn đồng
B. 50 triệu 640 nghìn đồng
C. 53 triệu 760 nghìn đồng
D. 48 triệu 480 nghìn đồng
Câu 283 : Cho hàm số $y = a x^{3} + b x^{2} + c x + d$ đạt cực trị tại các điểm $x_{1}, x_{2}$ thỏa mãn $x_{1} \in (- 1; 0), x_{2} \in (1; 2)$ . Biết hàm số đồng biến trên ( $x_{1}, x_{2}$ ). Đồ thị hàm số cắt trục tung tại điểm có tung độ âm. Trong các khẳng định sau, khẳng định nào đúng?

A. $a < 0, b > 0, c > 0, d < 0$
B. $a < 0, b < 0, c > 0, d < 0$
C. $a > 0, b > 0, c > 0, d < 0$
D. $a < 0, b > 0, c < 0, d < 0$
Câu 284 : Cho hàm số y = f(x) xác định và liên tục trên $ℝ$ thỏa mãn đồng thời các điều kiện sau: f(x) > 0 với $\forall x \in ℝ, f' (x) = - e^{x} . f^{2} (x)$ với $\forall x \in ℝ f (0) = \frac{1}{2}$ . Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ $x_{0} = \ln 2$ là:

A. $2 x + 9 y - 2 \ln 2 = 0$
B. $2 x - 9 y - 2 \ln 2 + 3 = 0$
C. $2 x - 9 y + 2 \ln 2 - 3 = 0$
D. $2 x + 9 y - 2 \ln 2 - 3 = 0$
Câu 285 : Trong đợt hội trại “Khi tôi 18” được tổ chức tại trường THPT XXX, Đoàn trường có thực hiện một dự án ảnh trưng bày trên một pano có dạng parabol như hình vẽ. Biết rằng Đoàn trường sẽ yêu cầu các lớp gửi hình dự thi và dán lên khu vực hình chữ nhật ABCD, phần còn lại sẽ được trang trí hoa văn cho phù hợp. 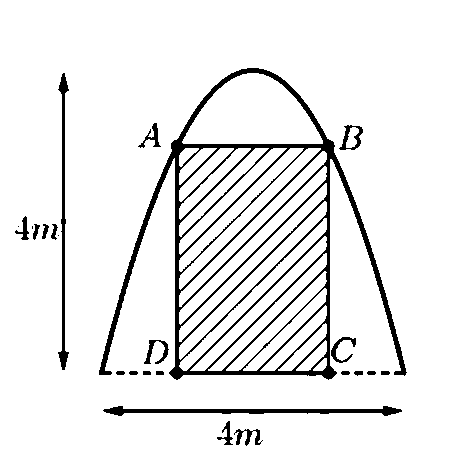Chi phí dán hoa văn là 200.000 đồng cho một $m^{2}$ bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm tròn đến hàng nghìn)?

A. 900.000 đồng
B. 1.232.000 đồng
C. 902.000 đồng
D. 1.230.000 đồng

Câu 286 : Tam giác ABC vuông tại B, AB = 10, BC = 4 . Gọi M,N lần lượt là trung điểm của AB, AC. Thể tích khối tròn xoay do hình thang vuông BMNC quay một vòng quanh MB là:

A. $\frac{40 π}{3}$
B. $\frac{20 π}{3}$
C. $\frac{120 π}{3}$
D. $\frac{140 π}{3}$
Câu 287 : Cho hàm số f(x). Biết hàm số y = f '(x) có đồ thị như hình bên. 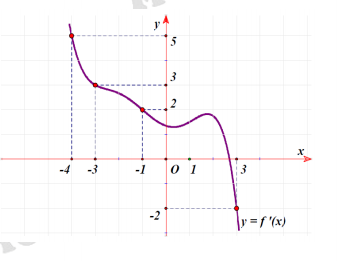Trên đoạn [-4;3] hàm số g(x) = 2f(x) + ${(1 - x)}^{2}$ đạt giá trị nhỏ nhất tại điểm

A. $x_{0} = - 4$
B. $x_{0} = - 1$
C. $x_{0} = 3$
D. $x_{0} = - 3$
Câu 288 : Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông ở A, AB = 2a, AC = a, AA' = 4a. M là điểm thuộc cạnh AA' sao cho MA' = 3MA . Tính khoảng cách giữa hai đường chéo nhau BC và C'M

A. $d = \frac{6 a}{7}$
B. $d = \frac{8 a}{7}$
C. $d = \frac{4 a}{3}$
D. $d = \frac{4 a}{7}$
Câu 289 : Cho dãy số $(u_{n})$ với $u_{1} = \sqrt{2}$ và $u_{n + 1} = \sqrt{2 + u_{n}}, n \geq 1$ . Chọn phát biểu đúng:

A. $(u_{n})$ không bị chặn trên
B. $u_{3} = \sqrt{2 + \sqrt{2 \sqrt{2}}}$
C. $(u_{n})$ là dãy giảm
D. $(u_{n})$ bị chặn

Câu 290 : Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số $y = |\frac{1}{4} x^{4} - \frac{19}{2} x^{2} + 30 x + m - 20|$ trên đoạn [0;2] không vượt quá 20. Tổng các phần tử của S bằng:

A. 210
B. 105
C. -195
D. 300
Câu 291 : Biết số phức z thỏa mãn $|z - 3 - 4 i| = \sqrt{5}$ và biểu thức $T = {|z + 2|}^{2} - {|z - i|}^{2}$ đạt giá trị lớn nhất. Tính $|z|$ .

A. $|z| = \sqrt{33}$
B. $|z| = 50$
C. $|z| = 10$
D. $|z| = 5 \sqrt{2}$
Câu 292 : Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số lập được từ tập hợp X = {1,2,3,4,5,6,7,8,9}. Chọn ngẫu nhiên một số từ S. Tính xác suất để số chọn được là số chia hết cho 6

A. $\frac{4}{27}$
B. $\frac{9}{28}$
C. $\frac{1}{9}$
D. $\frac{4}{9}$
Câu 293 : Cho hàm số $y = f (x) = - x^{3} + 6 x^{2} + 2$ có đồ thị (C) và điểm M(m;2). Gọi S là tập hợp các giá trị thực của m để qua M kẻ được đúng hai tiếp tuyến với đồ thị (C). Tổng các phần tử của S là:

A. $\frac{12}{3}$
B. $\frac{20}{3}$
C. $\frac{19}{3}$
D. $\frac{23}{3}$

Câu 294 : Phương trình $2 \log_{3} (c o t x) = \log_{2} (\cos x)$ có bao nhiêu nghiệm trong khoảng $(0; 2018 π)$ ?

A. 2018 nghiệm
B. 1008 nghiệm
C. 2017 nghiệm
D. 1009 nghiệm
Câu 295 : Một khối hình trụ có chiều cao bằng 3 lần đường kính của mặt đáy chứa đầy nước. Người ta đặt vào trong khối đó một khối cầu có đường kính bằng đường kính khối trụ và một khối nón có đỉnh tiếp xúc với khối cầu, đáy khối nón trùng với đáy trên của khối trụ (như hình vẽ).

A. $\frac{4}{9}$
B. $\frac{5}{9}$
C. $\frac{2}{3}$
D. $\frac{1}{2}$
Câu 296 : Tìm tất cả các giá trị thực của tham số m để hàm số $y = \ln (x^{2} - 2 m x + 4)$ xác định với mọi $x \in ℝ$ .

A. $m \in [- \infty; - 2] \cup [2; + \infty]$
B. $m \in [- 2; 2]$
C. $m \in (- \infty; - 2) \cup (2; + \infty)$
D. $m \in (- 2; 2)$
Câu 297 : Cho hai số thực dương a và b. Rút gọn biểu thức $A = \frac{a^{\frac{1}{3}} \sqrt{b} + b^{\frac{1}{3}} \sqrt{a}}{\sqrt[6]{a} + \sqrt[6]{b}}$ .

A. $A = \sqrt[6]{a b}$
B. $A = \sqrt[3]{a b}$
C. $A = \frac{1}{\sqrt[3]{a b}}$
D. $A = \frac{1}{\sqrt[6]{a b}}$

Câu 298 : Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc nhau và SA = SB = SC = a. Tính thể tích của khối chóp S.ABC.

A. $\frac{1}{3} a^{3}$
B. $\frac{1}{2} a^{3}$
C. $\frac{1}{6} a^{3}$
D. $\frac{2}{3} a^{3}$
Câu 299 : Trong không gian với hệ trục tọa độ Oxy, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là:

A. $D (- 1; 1; \frac{2}{3})$
B. $D (1; 3; 4)$
C. $D (1; 4; 4)$
D. $D (- 1; - 3; - 2)$
Câu 300 : Tập xác định của hàm số $y = \frac{1}{\sqrt{x^{2} - 4 x + 5}} + \log_{3} (x - 4)$ là

A. $D = (- 4; + \infty)$
B. $D = [4; + \infty)$
C. $D = (4; 5) \cup (5; + \infty)$
D. $D = (4; + \infty)$
Câu 301 : Trong không gian Oxyz, mặt phẳng (P):6x - 3y + 2z - 6 = 0. Tính khoảng cách d từ điểm M(1;-2;3) đến mặt phẳng (P).

A. $d = \frac{\sqrt{31}}{7}$
B. $d = \frac{12 \sqrt{85}}{85}$
C. $d = \frac{18}{7}$
D. $d = \frac{12}{7}$

Câu 302 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sinx trên đoạn $[- \frac{π}{2}; - \frac{π}{3}]$ lần lượt là

A. $- \frac{1}{2}; - \frac{\sqrt{3}}{2}$
B. $- \frac{\sqrt{3}}{2}; - 1$
C. $- \frac{\sqrt{3}}{2}; - 2$
D. $- \frac{\sqrt{2}}{2}; - \frac{\sqrt{3}}{2}$
Câu 303 : Cho số phức $w = 2 i - 3 + \frac{2}{i^{7}}$ . Tính môđun của số phức wi.

A. Không tồn tại
B. $|w i| = \sqrt{13}$
C. $|w i| = 5$
D. $|w i| = \sqrt{17}$
Câu 304 : Tính đạo hàm của hàm số $y = - x^{7} + 2 x^{5} + 3 x^{3}$

A. $y' = - x^{6} + 2 x^{4} + 3 x^{2}$
B. $y' = - 7 x^{6} - 10 x^{4} - 6 x^{2}$
C. $y' = 7 x^{6} - 10 x^{4} - 6 x^{2}$
D. $y' = - 7 x^{6} + 10 x^{4} + 9 x^{2}$
Câu 305 : Tính $L = l i m \frac{8 n^{5} - 2 n^{3} + 1}{4 n^{5} + 2 n^{2} + 1}$

A. $L = 2$
B. $L = 8$
C. $L = 1$
D. $L = 4$

Câu 306 : Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng (H) được giới hạn bởi các đường y = f(x) trục Ox và hai đường thẳng x = a,x = b (a < b) xung quanh trục Ox

A. $π \int_{a}^{b} f^{2} (x) d x$
B. $\int_{a}^{b} f^{2} (x) d x$
C. $π \int_{a}^{b} f (x) d x$
D. $2 π \int_{a}^{b} f^{2} (x) d x$
Câu 307 : Số nào sau đây lớn hơn 1

A. $\log_{0, 5} \frac{1}{8}$
B. $\log_{0, 2} 125$
C. $\log_{\frac{1}{6}} 36$
D. $\log_{0, 5} \frac{1}{2}$
Câu 308 : Cho hàm số $f (x) = \frac{4^{x} - 4^{- x}}{2}$ . Tính M = y' + yln4

A. $M = 4^{x}$
B. $M = 4^{- x}$
C. $M = 4^{x} \ln 4$
D. $M = 4^{- x} \ln 4$
Câu 309 : Gọi x, y là các số thực thỏa điều kiện $3 x - i y + 5 x y i = {(x + i y)}^{2}$ . Tìm tất cả các giá trị của y.

A. y = -1
B. y = 0
C. y = 3
D. $y = \frac{1}{3}$

Câu 310 : Tổng số đỉnh, số cạnh và số mặt của một hình lập phương là

A. 16
B. 26
C. 8
D. 24
Câu 311 : Trong không gian Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x + 4 y + 2 z - 3 = 0$ . Tính bán kính R của mặt cầu (S).

A. R = 3
B. R = 9
C. R = $3 \sqrt{3}$
D. R = $\sqrt{3}$
Câu 312 : Cho hình nón có độ dài đường sinh l = 2a, góc ở đỉnh của hình nón $2 β = 60 °$ . Tính thể tích V của khối nón đã cho

A. $V = π a^{3}$
B. $V = \frac{π a^{3}}{2}$
C. $V = \frac{π a^{3} \sqrt{3}}{3}$
D. $V = π a^{3} \sqrt{3}$
Câu 313 : Cho cấp số cộng $(u_{n})$ có $u_{4} = - 12, u_{14} = 18$ . Tính tổng 16 số hạng đầu tiên của cấp số cộng này.

A. $S_{16} = - 24$
B. $S_{16} = 26$
C. $S_{16} = - 25$
D. $S_{16} = 24$

Câu 314 : Cho hàm số y = f(x) có $\lim_{x \to + \infty} f (x) = 1$ và $\lim_{x \to - \infty} f (x) = - 1$ . Khẳng định nào sau đây là đúng?

A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 1 và y = -1
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 1 và y = -1
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang
D. Đồ thị hàm số đã cho không có tiệm cận ngang
Câu 315 : Cho hàm số $y = f (x) = \frac{2 \sqrt{1 + x} - \sqrt[3]{8 - x}}{x}$ . Tính $\lim_{x \to 0} f (x)$

A. $\frac{1}{12}$
B. $\frac{13}{12}$
C. $+ \infty$
D. $\frac{10}{11}$
Câu 316 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên SD = $\frac{3 a}{2}$ . Tính thể tích khối chóp S.ABCD theo a.

A. $\frac{1}{3} a^{3}$
B. $\frac{\sqrt{3}}{3} a^{3}$
C. $\frac{\sqrt{6}}{3} a^{3}$
D. $\frac{\sqrt{2}}{3} a^{3}$
Câu 317 : Tìm số nghiệm của phương trình $\log_{5} (1 + x^{2}) + \log_{\frac{1}{3}} (1 - x^{2}) = 0 .$

A. 0
B. 1
C. 2
D. 3

Câu 318 : Cho hàm số y = f(x). Hàm số y = f ' (x) có đồ thị như hình bên.

A. 3
B. 1
C. 0
D. 2
Câu 319 : Cho hàm số $y = \{\begin{array}{l} \frac{2 x + 6}{3 x^{2} - 27}, x \neq \pm 3 \\ - \frac{1}{9}, x = \pm 3 \end{array} .$ Mệnh đề nào sau đây đúng ?

A. Hàm số liên tục tại mọi điểm trừ các điểm x thuộc khoảng (-3;3)
B. Hàm số liên tục tại mọi điểm trừ điểm x = -3
C. Hàm số liên tục tại mọi điểm trừ điểm x = 3
D. Hàm số liên tục trên $ℝ$
Câu 320 : Cho khối hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACB’D’.

A. $\frac{7}{3}$
B. 3
C. $\frac{8}{3}$
D. 2
Câu 321 : Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số $y = 3 + \frac{1}{x - 3} .$

A. y = -3
B. x = 3
C. x = -3
D. y = 3

Câu 322 : Biết rằng đồ thị hàm số $y = x^{4} - 3 x^{2} + 5$ và đường thẳng y = 9 cắt nhau tại hai điểm phân biệt $A (x_{1}; y_{1}), B (x_{2}; y_{2})$ Tính $x_{1} + x_{2}$ .

A. $x_{1} + x_{2} = 3$
B. $x_{1} + x_{2} = 0$
C. $x_{1} + x_{2} = 18$
D. $x_{1} + x_{2} = 5$
Câu 323 : Hàm số nào trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây, không có cực trị?

A. $y = x^{3} + 3 x^{2} - 4 x + 1$
B. $y = - x^{4} - 4 x^{2} + 3$
C. $y = x^{3} - 3 x + 5$
D. $y = \frac{x + 4}{x - 1}$
Câu 324 : Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức $G (x) = 0, 024 x^{2} (30 - x),$ trong đó x là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp (x được tính bằng mg). Tìm lượng thuốc để tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất.

A. 20mg
B. 0,5mg
C. 2,8mg
D. 15mg
Câu 325 : Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a.

A. $V = \frac{\sqrt{2} a^{3}}{3}$
B. $V = \frac{\sqrt{2} a^{3}}{4}$
C. $V = \frac{\sqrt{3} a^{3}}{2}$
D. $V = \frac{\sqrt{3} a^{3}}{4}$

Câu 326 : Trong các dãy số ( $u_{n}$ ) cho dưới đây, dãy số nào có giới hạn khác 1?

A. $u_{n} = \frac{n {(n - 2018)}^{2017}}{{(n - 2017)}^{2018}}$
B. $u_{n} = n (\sqrt{n^{2} + 2020} - \sqrt{4 n^{2} + 2017})$
C. $u_{n} = \frac{1}{1.3} + \frac{1}{3.5} + . . . + \frac{1}{(2 n + 1) (2 n + 3)}$
D. $\{\begin{cases} u_{1} = 2018 \\ u_{n + 1} = \frac{1}{2} (u_{n} + 1), n \geq 1 \end{cases}$
Câu 327 : Đồ thị hàm số $y = x^{2} - x$ và đồ thị hàm số $y = 5 + \frac{3}{x}$ cắt nhau tại hai điểm A và B. Khi đó, độ dài AB là:

A. $A B = 8 \sqrt{5}$
B. $A B = 25$
C. $A B = 4 \sqrt{2}$
D. $A B = 10 \sqrt{2}$
Câu 328 : Cho hai số phức $z_{1} = 1 - i$ và $z_{2} = 2 + 3 i$ . Tính môđun của số phức $z_{2} - i z_{1} .$

A. $\sqrt{3}$
B. 5
C. $\sqrt{5}$
D. $\sqrt{13}$
Câu 329 : Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số $y = \frac{x^{3} - 3 x^{2} + 20}{x^{2} - 5 x - 14} .$

A. x = -2 và x = 7
B. x = -2
C. x = 2 và x = -7
D. x = 7

Câu 330 : Tìm tổng các nghiệm của phương trình $2^{2 x + 1} - 5 . 2^{x} + 2 = 0 .$

A. 0
B. $\frac{5}{2}$
C. 1
D. 2
Câu 331 : Cho mặt cầu $(S) : {(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 25$ và mặt phẳng $(α) : 2 x + y - 2 z + m = 0 .$ Các giá trị của m để $(α)$ và (S) không có điểm chung là:

A. $m \leq - 9 h o ặ c m \geq 21$
B. $m < - 9 h o ặ c m > 21$
C. $- 9 \leq m \leq 21$
D. $- 9 < m < 21$
Câu 332 : Cho điểm A(-3;2;4) gọi A,B, C lần lượt là hình chiếu của M trên trục Ox, Oy, Oz. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (ABC)

A. $6 x - 4 y - 3 z - 12 = 0$
B. $3 x - 6 y - 4 z + 12 = 0$
C. $4 x - 6 y - 3 z + 12 = 0$
D. $4 x - 6 y - 3 z - 12 = 0$
Câu 333 : Đồ thị hàm số $y = \frac{\sqrt{x^{2} - 4}}{x^{2} - 5 x + 6}$ có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

A. 1
B. 3
C. 4
D. 2

Câu 334 : Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y = $|f (x) + m|$ có ba điểm cực trị là

A. $m \leq - 1 h o ặ c m \geq 3 .$
B. $m = - 1 h o ặ c m = 3 .$
C. $m \leq - 3 h o ặ c m \geq 1 .$
D. $1 \leq m \leq 3 .$
Câu 335 : Tìm tập xác định D của hàm số $y = \log_{2017} {(x - 2)}^{4} + \log_{2018} (9 - x^{2}) .$

A. D = (-3;2)
B. D = (2;3)
C. D = (-3;3) $\ \{2\}$
D. D = [-3;3]
Câu 336 : Tìm hệ số của $x^{4}$ trong khai triển nhị thức Newton ${(2 x + \frac{1}{\sqrt[5]{x}})}^{n}$ với x > 0, biết n là số tự nhiên lớn nhất thỏa mãn $A_{n}^{5} \leq 18 A_{n - 2}^{4} .$

A. 8064
B. 3360
C. 13440
D. 15360
Câu 337 : Để đầu tư dự án trồng rau sạch theo công nghệ mới, bác A đã làm hợp đồng xin vay vốn ngân hàng với số tiền 100 triệu đồng với lãi suất x% trên một năm. Điều kiện kèm theo của hợp đồng là số tiền lãi tháng trước sẽ được tính làm vốn để sinh lãi cho tháng sau. Sau hai năm thành công với dự án rau sạch của mình, bác A đã thanh toán hợp đồng ngân hàng số tiền làm tròn là 129 512 000 đồng. Hỏi lãi suất trong hợp đồng giữa bác A và ngân hàng là bao nhiêu?

A. x = 14
B. x = 15
C. x = 13
D. x = 12

Câu 338 : Trong không gian với hệ trục Oxyz cho điểm A(2;1;3) và đường thẳng có phương trình $(d) : \frac{x - 1}{2} = \frac{y - 2}{- 1} = \frac{z}{1} .$ Mặt phẳng (P) chứa A và d. Viết phương trình mặt cầu tâm O tiếp xúc với mặt phẳng (P).

A. $x^{2} + y^{2} + z^{2} = \frac{12}{5}$
B. $x^{2} + y^{2} + z^{2} = 3$
C. $x^{2} + y^{2} + z^{2} = 6$
D. $x^{2} + y^{2} + z^{2} = \frac{24}{5}$
Câu 339 : Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;1;3), B(0;2;1), C(-2;0;-3). Điểm M thuộc Oz sao cho $|2 \vec{M A} + \vec{M B} + \vec{M C}|$ nhỏ nhất có tọa độ là:

A. (0;0;2)
B. (0;0;-1)
C. (0;0;1)
D. $(0; 0; \frac{1}{2})$
Câu 340 : Biết rằng $\int_{0}^{1} 3 e^{\sqrt{1 + 3 x}} d x = \frac{a}{5} e^{2} + \frac{b}{3} e + c$ . Tính $T = a + \frac{b}{2} + \frac{c}{3}$ .

A. $T = 6$
B. $T = 9$
C. $T = 10$
D. $T = 5$
Câu 341 : Cho bốn hàm số $y = {(\sqrt{3})}^{x} (1)$ , $y = {(\frac{1}{\sqrt{3}})}^{x} (2)$ , $y = 4^{x} (3), y = {(\frac{1}{4})}^{x} (4)$ có đồ thị là 4 đường cong theo phía trên đồ thị, thứ tự từ trái qua phải là $(C_{1}), (C_{2}), (C_{3}), (C_{4})$ như hình vẽ. Tương ứng hàm số - đồ thị đúng là

A. $(1) - (C_{2}), (2) - (C_{3}), (3) - (C_{4}), (4) - (C_{1})$
B. $(1) - (C_{1}), (2) - (C_{2}), (3) - (C_{3}), (4) - (C_{4})$
C. $(1) - (C_{4}), (2) - (C_{1}), (3) - (C_{3}), (4) - (C_{2})$
D. $(1) - (C_{4}), (2) - (C_{2}), (3) - (C_{3}), (4) - (C_{1})$

Câu 342 : Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Gọi BE và DF là hai đường cao của tam giác BCD. DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau?

A. $(A B E) ⊥ (A D C)$
B. $(A B D) ⊥ (A D C)$
C. $(A B C) ⊥ (D F K)$
D. $(D F K) ⊥ (A D C)$
Câu 343 : Cho hàm số $f (x) = \{\begin{array}{l} \frac{\sqrt{x + 4} - 2}{x}, x > 0 \\ m x + m + \frac{1}{4}, x \leq 0 \end{array}, m$ là tham số. Tìm giá trị của tham số m để hàm số có giới hạn tại x = 0.

A. m = 1
B. m = 0
C. $m = \frac{1}{2}$
D. $m = \frac{- 1}{2}$
Câu 344 : Tính $F (x) = \int x \sin x d x$ . Chọn kết quả đúng?

A. $F (x) = \frac{1}{4} (2 x \cos 2 x + \sin 2 x) + C$
B. $F (x) = - \frac{1}{4} (2 x \cos 2 x + \sin 2 x) + C$
C. $F (x) = - \frac{1}{4} (2 x \cos 2 x - \sin 2 x) + C$
D. $F (x) = \frac{1}{4} (2 x \cos 2 x - \sin 2 x) + C$
Câu 345 : Một cấp số nhân có số hạng đầu $u_{1} = 3$ , công bội q = 2. Biết $S_{n} = 765$ . Tìm n?

A. n = 7
B. n = 6
C. n = 8
D. n = 9

Câu 346 : Biến đổi $\int_{0}^{3} \frac{x}{1 + \sqrt{1 + x}} d x$ thành $\int_{1}^{2} f (t) d t$ với $t = \sqrt{1 + x}$ . Khi đó f(t) là hàm số nào trong các hàm số sau đây?

A. $f (t) = 2 t^{2} - 2 t$
B. $f (t) = t^{2} + t$
C. $f (t) = 2 t^{2} + 2 t$
D. $f (t) = t^{2} - t$
Câu 347 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AD = 2a, AB = a, cạnh bên SA = $a \sqrt{2}$ và vuông góc với mặt phẳng đáy (ABCD). Gọi M là trung điểm của cạnh BC. Tính bán kính hình cầu ngoại tiếp hình chóp S.AMD

A. $\frac{a \sqrt{6}}{6}$
B. $\frac{a \sqrt{6}}{4}$
C. $\frac{a \sqrt{6}}{2}$
D. $\frac{a \sqrt{6}}{3}$
Câu 348 : Từ các chữ số 0,1,2,3,4,5,6 có thể lập được bao nhiêu số có 5 chữ số khác nhau mà số đó nhất thiết có mặt các chữ số 1,2,5?

A. 684
B. 648
C. 846
D. 864
Câu 349 : Hỏi có bao nhiêu giá trị nguyên của m để bất phương trình $\log_{2}^{2} x + m \log_{2} x - m \geq 0$ nghiệm đúng với mọi giá trị của $x \in (0; + \infty)$ ?

A. Có 4 giá trị nguyên
B. Có 6 giá trị nguyên
C. Có 5 giá trị nguyên
D. Có 7 giá trị nguyên

Câu 350 : Cho hàm số $y = f (x) = a x^{3} + b x^{2} + c x + d (a, b, c \in ℝ, a \neq 0)$ có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y = f '(x) cho bởi hình vẽ dưới đây. 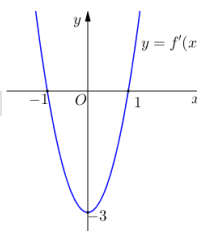Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.

A. S = 9
B. $S = \frac{5}{4}$
C. $S = \frac{21}{4}$
D. $S = \frac{27}{4}$
Câu 351 : Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d : \frac{x}{1} = \frac{y}{2} = \frac{z - 1}{- 1}$ và $d' : \{\begin{cases} x = 1 - 3 t \\ y = 1 + 2 t \\ z = 1 - t \end{cases}$ . Mặt phẳng (P) chứa d, tạo với đường thẳng d¢ một góc lớn nhất đi qua điểm nào dưới đây?

A. M(-1;2;1)
B. N(1;2;-3)
C. P(1;1;1)
D. Q(1;0;-4)
Câu 352 : Cho hàm số $y = |x^{3} - 3 x - m|$ . Có bao nhiêu giá trị nguyên của m để hàm số có 5 điểm cực trị?

A. 1
B. 2
C. 3
D. 4
Câu 353 : Một công ty dự kiến chi 1 tỷ đồng để sản xuất các thùng đựng sơn hình trụ có dung tích 5 lít. Biết rằng chi phí để làm mặt xung quanh của thùng đó là 100 000đ m/ $m^{2}$ chi phí để làm mặt đáy là 120 000đ m/ $m^{2}$ . Hãy tính số thùng sơn tối đa mà công ty đó sản xuất được (giả sử chi phí cho các mối nối không đáng kể).

A. 58135 thùng
B. 57582 thùng
C. 18209 thùng
D. 12525 thùng

Câu 354 : Cho y = f(x) là hàm số chẵn, có đạo hàm trên đoạn [-6;6]. Biết rằng $\int_{- 1}^{2} f (x) d x = 8$ và $\int_{1}^{3} f (- 2 x) d x = 3$ . Tính $I = \int_{- 1}^{6} f (x) d x$

A. I = 11
B. I = 5
C. I = 14
D. I = 2
Câu 355 : Một nguyên hàm của $f (x) = (2 x - 1) e^{\frac{1}{x}}$ là $F (x) = (a x^{2} + b x + c + \frac{d}{x}) e^{\frac{1}{x}} .$ Tính $a + b + c + d$

A. 1
B. 3
C. 0
D. 2
Câu 356 : Cho mặt cầu (S) bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất

A. $h = R \sqrt{2}$
B. $h = \frac{R}{2}$
C. $h = \frac{R \sqrt{2}}{2}$
D. $h = R$
Câu 357 : Tập giá trị của hàm số $\frac{\cos x + 1}{\sin x + 1}$ trên $[0; \frac{π}{2}]$ là:

A. $[\frac{1}{2}; 2]$
B. $(\frac{1}{2}; 2]$
C. $[\frac{1}{2}; 2)$
D. $(\frac{1}{2}; 2)$

Câu 358 : Đội thanh niên xung kích của trường THPT Moon.vn có 12 học sinh gồm 5 học sinh khối 12, 4 học sinh khối 11 và 3 học sinh khối 10. Chọn ngẫu nhiên 4 học sinh để làm nhiệm cụ mỗi buổi sáng. Tính xác suất sao cho 4 học sinh được chọn thuộc không quá 2 khối.

A. $\frac{5}{11}$
B. $\frac{6}{11}$
C. $\frac{21}{22}$
D. $\frac{15}{22}$
Câu 359 : Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $y = \frac{1 + \sqrt{x + 1}}{\sqrt{x^{2} - (1 - m) x + 2 m}}$ có hai tiệm cận đứng?

A. 0
B. 2
C. 3
D. 1
Câu 360 : Cho hàm số y = f(x) xác định trên $ℝ$ và có đồ thị hàm số y = f '(x) như hình vẽ bên. 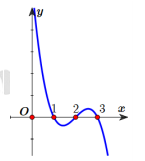Xét các khẳng định sau:

A. 1
B. 3
C. 2
D. 0
Câu 361 : Cho hàm số $y = \frac{2}{3} x^{3} + (m + 1) x^{2} + (m^{2} + 4 m + 3) x - 3$ (m là tham số thực). Tìm điều kiện của m để hàm số có cực đại và cực tiểu và các điểm cực trị của hàm số nằm bên phải của trục tung

A. $- 5 < m < - 1$
B. $- 5 < m < - 3$
C. $- 3 < m < - 1$
D. $[\begin{array}{l} m > - 1 \\ m < - 5 \end{array}$

Câu 362 : Tứ diện OABC có OA = OB = OC = 1 và $O A ⊥ O B .$ Tìm góc giữa OC và (OAB) để tứ diện có thể tích là $\frac{1}{12}$

A. 30 $°$
B. 45 $°$
C. 60 $°$
D. 90 $°$
Câu 363 : Cho tứ diện S.ABC trên đoạn thẳng SA, SB, SC lần lượt lấy các điểm M, N, P sao cho SM = 5 MA, SN = 2NB và SP = kPC. Kí hiệu $V_{T}$ là thể tích của khối đa diện T. Biết rằng $V_{S M N P} = \frac{1}{2} V_{S A B C} .$ Tìm k?

A. $k = \frac{1}{2}$
B. k = 9
C. k = 5
D. k = 4
Câu 364 : Xét tứ diện AB = BC = CD = DA = 1 và AC = BD thay đổi. Giá trị lớn nhất của thể tích tứ diện ABCD bằng

A. $\frac{2 \sqrt{3}}{27}$
B. $\frac{4 \sqrt{3}}{27}$
C. $\frac{2 \sqrt{3}}{9}$
D. $\frac{4 \sqrt{3}}{9}$
Câu 365 : Một người nông dân có một tấm cót hình chữ nhật có chiều dài $12 π (dm)$ , chiều rộng 1 (m). Người nông dân muốn quây tấm cót thành một chiếc bồ đựng thóc không có đáy, không có nắp đậy, có chiều cao bằng chiều rộng của tấm cót theo các hình dáng sau:

A. (I)
B. (II)
C. (III)
D. (IV)

Câu 366 : Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số (x;y) thỏa mãn $e^{2 x + y + 1} - e^{3 x + 2 y} = x + y + 1$ đồng thời thỏa mãn $\log_{2}^{2} (2 x + y - 1) - (m + 4) \log_{2} x + m^{2} + 4 = 0$ .

A. 3
B. 4
C. 5
D. 6
Câu 367 : Bác An có ba tấm lưới mắt cáo, mỗi tấm có chiều dài 4 m. Bác muốn rào một phần vườn của nhà bác dọc theo bờ tường (bờ tường ngăn đất nhà bác với đất nhà hàng xóm) theo hình thang cân ABCD (như hình vẽ) để trồng rau (AB là phần tường không cần phải rào). Bác An rào được phần đất vườn có diện tích lớn nhất gần với giá trị nào nhất sau đây?

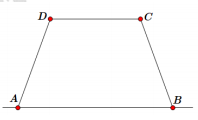
A. 28 $m^{2}$
B. 7 $m^{2}$
C. 35 $m^{2}$
D. 21 $m^{2}$
Câu 368 : Tính giá trị của biểu thức $P = x^{2} + y^{2} - x y + 1$ biết rằng $4^{x^{2} + \frac{1}{x^{2}} - 1} = \log_{2} [14 - (y - 2) \sqrt{y + 1}]$ với $x \neq 0; - 1 \leq y \leq \frac{13}{2}$ .

A. P = 4
B. P = 2
C. P = 1
D. P = 3
Câu 369 : Cho hàm số $f (x) = \frac{4^{x}}{4^{x} + 2} .$

A. 2014
B. 2015
C. 1008
D. 1007

Câu 370 : Cho dãy số $(u_{n})$ thỏa mãn $\log^{3} u_{1} - 2 \log^{2} u_{1} + \log u_{1} - 2 = 0$ với mọi $n \geq 1$ . Giá trị nhỏ nhất của n để $u_{n} > 100^{100} - 10$ bằng:

A. 326
B. 327
C. 225
D. 226
Câu 371 : Số các giá trị nguyên của tham số $m \in [- 2018; 2018]$ để PT $x^{2} + (m + 2) x + 4 = (m - 1) \sqrt{x^{3} + 4 x}$ có nghiệm là

A. 2016
B. 2010
C. 2012
D. 2014
Câu 372 : Cho hàm số y = f(x) xác định trên $ℝ$ và có đạo hàm f '(x) thỏa mãn $f' (x) = (1 - x) (x + 2) . g (x) + 2018$ trong đó $g (x) < 0, \forall x \in ℝ$ . Hàm số $y = f (1 - x) + 2018 x + 2019$ nghịch biến trên khoảng nào?

A. $(1; + \infty)$
B. $(0; 3)$
C. $(- \infty; 3)$
D. $(3; + \infty)$
Câu 373 : Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có $B A C = 75 °, A C B = 60 °$ . Kẻ $B H ⊥ A C .$ Quay tam giác ABC quanh trục AC thì $∆ B H C$ tạo thành hình nón xoay có diện tích xung quanh bằng?

A. $\frac{{πR}^{2} \sqrt{3}}{4} . {(\sqrt{3} + 1)}^{2}$
B. $\frac{{πR}^{2} \sqrt{3}}{4}$
C. $\frac{{πR}^{2} \sqrt{3}}{4} . (\sqrt{2} + 1)$
D. $\frac{{πR}^{2} \sqrt{3}}{4} . (\sqrt{3} + 1)$

Câu 374 : Cho tứ diện ABCD có CD = 3. Hai tam giác ACD, BCD có diện tích lần lượt là 15 và 10. Biết thể tích của tứ diện ABCD bằng 20. Tính cotan của góc giữa hai mặt phẳng (ACD) và (BCD)?

A. $\frac{3}{4}$
B. $\frac{3}{5}$
C. $\frac{5}{3}$
D. $\frac{4}{3}$
Câu 375 : Cho số phức z thỏa $4 |z + i| + 3 |z - i| = 10$ . Giá trị nhỏ nhất của $|z|$ bằng

A. $\frac{1}{2}$
B. $\frac{5}{7}$
C. $\frac{3}{2}$
D. 1
Câu 376 : Cho hàm số f(x) có đạo hàm liên tục trên và thỏa mãn $f (x) > 0, \forall \in ℝ$ . Biết f(0) = 1 và $\frac{f' (x)}{f (x)} = 2 - 2 x$ . Tìm các giá trị thực của tham số m để phương trình f(x) = m có hai nghiệm thực phân biệt.

A. m > e
B. $0 < m \leq 1$
C. 0 < m < e
D. 1 < m < e
Câu 377 : Trong không gian với hệ tọa độ Oxyz, xét mặt cầu (S) đi qua hai điểm A(1;6;2), B(3;0;0) và có tâm thuộc mặt phẳng (P):x - y + 2 =0. Bán kính mặt cầu (S) có giá trị nhỏ nhất là:

A. $\frac{\sqrt{534}}{4}$
B. $\frac{\sqrt{426}}{6}$
C. $\frac{\sqrt{530}}{4}$
D. $\frac{\sqrt{218}}{6}$

Câu 378 : Cho hàm số y = f(x) xác định và liên tục trên $ℝ$ thỏa mãn đồng thời các điều kiện sau: $\{\begin{cases} f (x) > 0, \forall \in ℝ \\ f' (x) = - e^{x} . f^{2} (x), \forall \in ℝ \\ f (0) = \frac{1}{2} \end{cases}$

A. $\ln 2 + \frac{1}{2}$
B. $\frac{1}{4}$
C. $\frac{1}{3}$
D. $\ln^{2} 2 + \frac{1}{2}$
Câu 379 : Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?

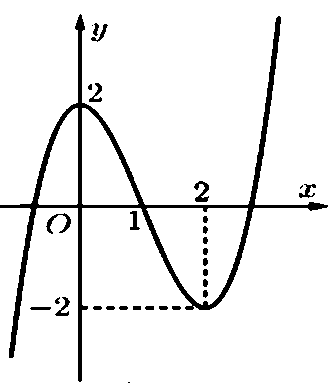
A. $y = x^{3} - 3 x^{2} + 2$
B. $y = x^{3} + 3 x^{2} + 2$
C. $y = - x^{3} + 3 x^{2} + 2$
D. $y = x^{3} - 3 x^{2} + 1$
Câu 380 : Một khối trụ có thể tích bằng $25 π$ . Nếu chiều cao khối trụ tăng lên năm lần và giữ nguyên bán kính đáy thì được khối trụ mới có diện tích xung quanh bằng $25 π$ . Bán kính đáy của khối trụ ban đầu là

A. r = 10
B. r = 5
C. r = 2
D. r = 15
Câu 381 : Cho một đa giác đều 20 đỉnh nội tiếp trong đường tròn O. Chọn ngẫu nhiên 4 đỉnh của đa giác đó. Tính xác suất sao cho 4 đỉnh được chọn là 4 đỉnh của một hình chữ nhật

A. $\frac{3}{323}$
B. $\frac{4}{9}$
C. $\frac{2}{969}$
D. $\frac{7}{216}$

Câu 382 : Cho hình chóp S.ABCD có đáy là hình vuông; SA = AB = a và $S A ⊥ (A B C D) .$ Gọi M là trung điểm AD, tính khoảng cách giữa hai đường thẳng SC và BM

A. $\frac{a \sqrt{14}}{6}$
B. $\frac{6 a}{\sqrt{14}}$
C. $\frac{a \sqrt{14}}{2}$
D. $\frac{2 a}{\sqrt{14}}$
Câu 383 : Cho hàm số $y = f (x) = \{\begin{cases} \frac{e^{a x} - e^{3 x}}{2 x} k h i x \neq 0 \\ \frac{1}{2} k h i x = 0 \end{cases} .$ Tìm giá trị của a để hàm số f(x) liên tục tại điểm x = 0.

A. a = 2
B. a = 4
C. $a = - \frac{1}{4}$
D. $a = - \frac{1}{2}$
Câu 384 : Cho hình chóp S.ABC có độ dài cạnh SA = BC = x, SB = AC = y, SC = AB = z thỏa mãn điều kiện $x^{2} + y^{2} + z^{2} = 9$ . Tính giá trị lớn nhất của thể tích khối chóp S.ABC.

A. $\frac{3 \sqrt{6}}{8}$
B. $\frac{3 \sqrt{6}}{4}$
C. $\frac{\sqrt{6}}{4}$
D. $\frac{2 \sqrt{6}}{5}$
Câu 385 : Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình $(1 - m^{2}) 2 n . x + 4 m n . y + (1 + m^{2}) (1 - n^{2}) . z + 4 (m^{2} n^{2} + m^{2} + n^{2} + 1) = 0,$ với m, n là tham số thực tùy ý. Biết rằng mặt phẳng (P) luôn tiếp xúc với một mặt cầu cố định khi m, n thay đổi. Tìm bán kính mặt cầu đó?

A. 1
B. 2
C. 3
D. 4

Câu 386 : Cho hai số phức $z_{1}, z_{2}$ thỏa mãn $|z_{1}| = |z_{2}| = |z_{1} - z_{2}| = 1 .$ Tính giá trị của biểu thức $P = {(\frac{z_{1}}{z_{2}})}^{2} + {(\frac{z_{2}}{z_{1}})}^{2} .$

A. P = 1 - i
B. P = -1 - i
C. P = -1
D. P = 1 + i
Câu 387 : Cho hàm số f(x) liên tục trên $ℝ^{+}$ thỏa mãn $f' (x) \geq x + \frac{1}{x}, \forall x \in ℝ^{+}$ và f(1) = 1. Tính giá trị nhỏ nhất của f(2).

A. 3
B. 2
C. $\frac{5}{2} + \ln 2$
D. 4
Câu 388 : Hàm số y = f(x) có đúng 3 điểm cực trị là -2;-1 và 0. Hỏi hàm số $y = f (x^{2} - 2 x)$ có bao nhiêu điểm cực trị?

A. 3
B. 4
C. 5
D. 6
Câu 389 : Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là $V = π$ tìm giá trị lớn nhất của biểu thức P = R + 2r.

A. $2 \sqrt{3}$
B. 3
C. $3 \sqrt{3}$
D. 2

Câu 390 : Có tất cả bao nhiêu cặp số thực (x,y) thỏa mãn đồng thời các điều kiện $3^{|x^{2} - 2 x - 3| - \log_{3} 5} = 5^{- (y + 4)}$ và $4 |y| - |y - 1| + {(y + 3)}^{2} \leq 8$ ?

A. 3
B. 2
C. 1
D. 4
Câu 391 : Cho hàm số y = f(x) với f(0) = f(1) = 1. Biết rằng: $\int_{0}^{1} e^{x} [f (x) + f' (x)] d x = a e + b .$

A. $Q = 2^{2017} + 1$
B. $Q = 2$
C. $Q = 0$
D. $Q = 2^{2017} - 1$
Câu 392 : Cho hình nón có bán kính đường tròn đáy là 6cm và diện tích hình tròn đáy bằng $\frac{3}{5}$ diện tích xung quanh của hình nón. Tính thể tích V khối nón

A. $V = 120 π ({cm}^{3})$
B. $V = 64 π ({cm}^{3})$
C. $V = 96 π ({cm}^{3})$
D. $V = 288 π ({cm}^{3})$
Câu 393 : Tìm cực tiểu của hàm số $y = - x^{3} + 6 x^{2} + 15 x + 10$

A. 5
B. 110
C. 2
D. -1

Câu 394 : Đồ thị của hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?

A. $y = \frac{2 x - 3}{3 x - 1}$
B. $y = \frac{- 2 x + 3}{x + 1}$
C. $y = \frac{3 x + 4}{x - 1}$
D. $y = \frac{4 x + 1}{x + 2}$
Câu 395 : Tính thể tích V của khối lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng 2a

A. $V = \frac{a^{3} \sqrt{3}}{2}$
B. $V = \frac{a^{3} \sqrt{3}}{6}$
C. $V = \frac{2 a^{3} \sqrt{3}}{3}$
D. $V = 2 a^{3} \sqrt{3}$
Câu 396 : Kí hiệu (H) là hình phẳng giới hạn bởi đường cong y =tan x trục hoành và hai đường thẳng x = 0; x = $\frac{π}{4}$ . Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox

A. $V = - π (1 - \frac{π}{4})$
B. $V = (1 + \frac{π}{4})$
C. $V = π (1 - \frac{π}{4})$
D. $V = π (2 - \frac{π}{4})$
Câu 397 : Trong không gian với hệ trục tọa độ Oxyz, cho A(1;2;-5), B(-3;0;1). Viết phương trình mặt cầu (S) có đường kính là AB.

A. $(S) : {(x + 2)}^{2} + {(y + 1)}^{2} + {(z - 3)}^{2} = 14$
B. $(S) : {(x - 1)}^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 56$
C. $(S) : {(x + 1)}^{2} + {(y - 1)}^{2} + {(z + 2)}^{2} = 14$
D. $(S) : {(x + 1)}^{2} + {(y - 1)}^{2} + {(z + 2)}^{2} = 56$

Câu 398 : Cho số phức z thỏa mãn $\frac{30 i}{1 - z} = 9 - 3 i$ . Gọi M là điểm biểu diễn số phức z. Tìm tung độ của M

A. 2
B. 3
C. -3
D. -1
Câu 399 : Trong không gian với hệ trục tọa độ Oxyz, gọi H là hình chiếu vuông góc của điểm A(-3;-1;-1) lên mặt phẳng (P): 2x + y + z - 4 = 0. Tìm tọa độ điểm H

A. H(2;0;0)
B. H(1;2;0)
C. H(1;1;1)
D. $H (\frac{1}{2}; 1; 2)$
Câu 400 : Gọi M, N là giao điểm của đường thẳng (d):y = x + 1 và đường cong $(C) : y = \frac{2 x + 4}{x - 1}$ . Hoành độ trung điểm I của đoạn thẳng MN bằng

A. $- \frac{5}{2}$
B. 2
C. $\frac{5}{2}$
D. 1
Câu 401 : Cho ba số x;5;2y lập thành cấp số cộng và ba số x;4;2y lập thành cấp số nhân thì $|x - 2 y|$ bằng

A. $|x - 2 y| = 8$
B. $|x - 2 y| = 9$
C. $|x - 2 y| = 6$
D. $|x - 2 y| = 10$

Câu 402 : Số giá trị nguyên dương của tham số m để phương trình $4 \sqrt{3} \cos x + \sin x + 2 m - 1 = 0$ có nghiệm là

A. 6
B. 5
C. 4
D. 3
Câu 403 : Trong các hàm số sau, hàm số nào đồng biến trên tập xác định của nó?

A. $y = {(\frac{3}{5})}^{x}$
B. $y = {(\frac{3}{2})}^{- x}$
C. $y = \log_{\frac{1}{2}} (x + 1)$
D. $y = {(\frac{2}{3})}^{1 - x}$
Câu 404 : Cho hình nón có bán kính đáy là $r = \sqrt{2}$ và độ dài đường sinh l = 4. Tính diện tích xung quanh S của hình nón đã cho

A. $S = 16 π$
B. $S = 8 \sqrt{2} π$
C. $S = 16 \sqrt{2} π$
D. $S = 4 \sqrt{2} π$
Câu 405 : Tiếp tuyến với đồ thị hàm số $y = x^{3} - 4 x + 1$ tại điểm có hoành độ bằng 2 có phương trình là

A. $y = - 8 x + 17$
B. $y = 8 x - 16$
C. $y = 8 x + 15$
D. $y = 8 x - 15$

Câu 406 : Hàm số nào sau đây không phải là một nguyên hàm của hàm số $f (x) = {(2 x - 3)}^{3}$ ?

A. $F (x) = \frac{{(2 x - 3)}^{4}}{8} + 8$
B. $F (x) = \frac{{(2 x - 3)}^{4}}{8} - 3$
C. $F (x) = \frac{{(2 x - 3)}^{4}}{8}$
D. $F (x) = \frac{{(2 x - 3)}^{4}}{4}$
Câu 407 : Cho hàm số f(x) thỏa mãn đồng thời các điều kiện f '(x) = x + sinx và f(0) = 1. Tìm f(x)

A. $f (x) = \frac{x^{2}}{2} - \cos x + 2$
B. $f (x) = \frac{x^{2}}{2} - \cos x - 2$
C. $f (x) = \frac{x^{2}}{2} + \cos x$
D. $f (x) = \frac{x^{2}}{2} + \cos x + \frac{1}{2}$
Câu 408 : Tính diện tích S của hình phẳng giới hạn bởi các đường $y = e^{x}, y = 2, x = 0$ và x = 1.

A. $S = 4 \ln 2 + e - 5$
B. $S = 4 \ln 2 + e - 6$
C. $S = e^{2} - 7$
D. $S = e - 3$
Câu 409 : Cho các số thực dương a, b thỏa mãn $\log_{2} a = x; \log_{2} b = y$ . Tính $P = \log_{2} (a^{2} b^{3})$

A. $P = x^{2} y^{3}$
B. $P = x^{2} + y^{3}$
C. $P = 6 x y$
$P = 2 x + 3 y$

Câu 410 : Cho các số tự nhiên m n, thỏa mãn đồng thời các điều kiện $C_{m}^{2} = 153$ và $C_{m}^{n} = C_{m}^{n + 2}$ . Khi đó m + 2 bằng

A. 25
B. 24
C. 26
D. 23
Câu 411 : Tính thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x = $π$ , biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ $x (0 \leq x \leq π)$ là một tam giác đều cạnh là $2 \sqrt{\sin x}$

A. $V = 3$
B. $V = 3 π$
C. $V = - 2 π \sqrt{3}$
D. $V = 2 \sqrt{3}$
Câu 412 : Cho cấp số cộng có tổng n số hạng đầu là $S_{n} = 3 n^{2} + 4 n, n \in ℕ *$ . Giá trị của số hạng thứ 10 của cấp số cộng là

A. $u_{10} = 55$
B. $u_{10} = 67$
C. $u_{10} = 61$
D. $u_{10} = 59$
Câu 413 : Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau

A. $\underset{(- 1; + \infty)}{m i n} f (x) = f (0)$
B. $\underset{(0; + \infty)}{m a x} f (x) = f (1)$
C. $\underset{(- 1; 1)}{m a x} f (x) = f (0)$
D. $\underset{(- \infty; - 1)}{m i n} f (x) = f (- 1)$

Câu 414 : Tổng của tất cả các số tự nhiên n thỏa mãn $\frac{1}{C_{n}^{1}} - \frac{1}{C_{n + 1}^{2}} = \frac{7}{6 C_{n + 4}^{1}}$ là

A. 13
B. 11
C. 10
D. 12
Câu 415 : Với hai số thực bất kì $a \neq 0, b \neq 0$ khẳng định nào sau đây là khẳng định sai?

A. $\log (a^{2} b^{2}) = 2 \log (a b)$
B. $\log (a^{2} b^{2}) = 3 \log \sqrt[3]{a^{2} b^{2}}$
C. $\log (a^{2} b^{2}) = \log (a^{4} b^{6}) - \log (a^{2} b^{4})$
D. $\log (a^{2} b^{2}) = \log a^{2} + \log b^{2}$
Câu 416 : Từ các chữ số 0; 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên chẵn có 3 chữ số?

A. 210
B. 105
C. 168
D. 145
Câu 417 : Cho hình phẳng (H) được giới hạn bởi đồ thị của hai hàm số $f (x_{1})$ và $f (x_{2})$ liên tục trên đoạn [a;b] và hai đường thẳng x = a,x = b (tham khảo hình vẽ). Công thức tính diện tích của (H) là

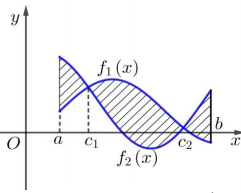
A. $S = \int_{a}^{b} |f_{1} (x) - f_{2} (x)| d x$
B. $S = \int_{a}^{b} [f_{1} (x) - f_{2} (x)] d x$
C. $S = \int_{a}^{b} |f_{1} (x) + f_{2} (x)| d x$
D. $S = \int_{a}^{b} f_{2} (x) - f_{1} (x) d x$

Câu 418 : Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kĩ sư theo phương thức sau: Mức lương của quý làm việc đầu tiên cho công ti là 4, 5 triệu đồng/quý, và kể từ quý làm việc thứ hai, mức lương sẽ được tăng thêm 0,3 triệu đồng mỗi quý. Hãy tính tổng số tiền lương một kĩ sư được nhận sau 3 năm làm việc cho công ti

A. 83,7 (triệu đồng)
B. 78,3 (triệu đồng)
C. 73,8 (triệu đồng).
D. 87,3 (triệu đồng)
Câu 419 : Cho hàm số y = f(x) xác định và liên tục trên $ℝ$ và có bảng biến thiên như hình bên. Khẳng định nào sau đây sai?

A. M(0;-3) là điểm cực tiểu của hàm số
B. Đồ thị hàm số có hai điểm cực đại và một điểm cực tiểu
C. f(2) được gọi là giá trị cực đại của hàm số
D. $x_{0} = 2$ được gọi là điểm cực đại của hàm số
Câu 420 : Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \frac{x + 1}{2} = \frac{y}{1} = \frac{z - 2}{1}$ và mặt phẳng (P) có phương trình x + y - 2z +5 = 0 và A(1;-1;2). Đường thẳng D cắt d và (P) lần lượt tại M và N sao cho A là trung điểm đoạn thẳng MN. Một vectơ chỉ phương của D là:

A. $\vec{a} = (2; 3; 2)$
B. $\vec{a} = (1; - 1; 2)$
C. $\vec{a} = (- 3; 5; 1)$
D. $\vec{a} = (4; 5; - 13)$
Câu 421 : Cho hàm số $y = x^{3} + 3 m x^{2} + (m + 1) x + 1$ có đồ thị (C). Biết rằng khi $m = m_{0}$ thì tiếp tuyến với đồ thị (C) tại điểm có hoành độ bằng $x_{0} = - 1$ đi qua điểm A(1;3). Khẳng định nào sau đây đúng?

A. $- 1 < m_{0} < 0$
B. $0 < m_{0} < 1$
C. $1 < m_{0} < 2$
D. $- 2 < m_{0} < - 1$

Câu 422 : Cho hàm số $y = x^{3} - 3 x + 2$ có đồ thị (C). Tổng các hệ số góc của các tiếp tuyến với (C) tại giao điểm của (C) với trục hoành bằng:

A. 9
B. 11
C. 0
D. -15
Câu 423 : Tìm giá trị lớn nhất của hàm số f(x) = sinx + cos2x trên $[0; π]$ là

A. $\frac{9}{8}$
B. $\frac{5}{4}$
C. 2
D. 1
Câu 424 : Tìm tất cả các giá trị của tham số a để hàm số $y = x^{3} + 3 \sqrt{3} a x$ có cực đại, cực tiểu và đường thẳng đi qua các điểm cực đại, cực tiểu của đồ thị hàm số đi qua gốc tọa độ

A. a < -1
B. a < 0
C. -1 < a < 0
D. a > 0
Câu 425 : Cho hình lăng trụ tam giác đều ABC.A’B’C’ có độ dài cạnh đáy bằng a và chiều cao bằng h. Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho

A. $V = \frac{{πa}^{2} h}{9}$
B. $V = \frac{a^{2} h}{9}$
C. $V = \frac{{πa}^{2} h}{3}$
D. $V = 3 {πa}^{2} h$

Câu 426 : Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0;2-2;) và B(2;2;-4). Giả sử I(a;b;c) là tâm đường tròn ngoại tiếp tam giác OAB. Tính $T = a^{2} + b^{2} + c^{2}$

A. T = 8
B. T = 2
C. T = 6
D. T = 14
Câu 427 : Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi K là trung điểm của DD¢. Khoảng cách giữa hai đường thẳng chéo nhau CK và AD¢ bằng:

A. $\frac{a \sqrt{3}}{3}$
B. $\frac{a \sqrt{3}}{2}$
C. $\frac{2 a \sqrt{3}}{3}$
D. $\frac{a}{3}$
Câu 428 : Gọi S là tập hợp các giá trị của tham số m để hàm số $y = \frac{1}{3} x^{3} + (m + 1) x^{2} + 4 x + 7$ nghịch biến trên một đoạn có độ dài bằng $2 \sqrt{5}$ . Tính tổng tất cả phần tử của S?

A. 4
B. 2
C. -1
D. -2
Câu 429 : Cho hình chóp S.ABC có $\hat{B S C} = 12 °, \hat{C S A} = 60 °, \hat{A S B} = 90 °$ và SA = SB = SC. Gọi I là hình chiếu vuông góc của S lên mặt phẳng (ABC). Khẳng định nào sau đây đúng?

A. I là trung điểm AB
B. I là trọng tâm tam giác ABC.
C. I là trung điểm AC
D. I là trung điểm BC

Câu 430 : Có 11 chiếc thẻ được đánh số từ 1 đến 11, người ta rút ngẫu nhiên hai thẻ khác nhau. Xác suất để rút được hai thẻ mà tích hai số được đánh trên thẻ là số chẵn bằng

A. $\frac{9}{11}$
B. $\frac{3}{11}$
C. $\frac{2}{11}$
D. $\frac{8}{11}$
Câu 431 : Trong không gian Oxyz, cho hai đường thẳng $∆_{1} : \frac{x - 4}{3} = \frac{y - 1}{- 1} = \frac{z + 5}{- 2}$ và $∆_{2} : \frac{x - 2}{1} = \frac{y + 3}{3} = \frac{z}{1}$ . Giả sử $M \in ∆_{1}, N \in ∆_{2}$ sao cho MN là đoạn vuông góc chung của hai đường thẳng $∆_{1}$ và $∆_{2}$ . Tính $\vec{M N}$ .

A. $\vec{M N} (5; - 5; 10)$
B. $\vec{M N} (2; - 2; 4)$
C. $\vec{M N} (3; - 3; 6)$
D. $\vec{M N} (1; - 1; 2)$
Câu 432 : Cho tứ diện ABCD có AB = CD = a. Gọi M và N lần lượt là trung điểm của AD và BC. Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng $30 °$ .

A. $M N = \frac{a}{2}$
B. $M N = \frac{a \sqrt{3}}{2}$
C. $M N = \frac{a \sqrt{3}}{3}$
D. $M N = \frac{a}{4}$
Câu 433 : Biết tập hợp các giá trị của tham số m để bất phương trình $4^{\sin^{2} x} + 5^{\cos^{2} x} \leq m . 7^{\cos^{2} x}$ có nghiệm là $[\frac{a}{b}; + \infty)$ với a, b là các số nguyên dương và $\frac{a}{b}$ là phân số tối giản. Khi đó giá trị S = a + b bằng:

A. S = 13
B. S = 15
C. S = 9
D. S = 11

Câu 434 : Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc vào thời gian t(h) có đồ thị vận tốc như hình bên. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh I(2;5) và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường mà vật di chuyển được trong 3 giờ đó

A. 15 (km)
B. $\frac{32}{3} (k m)$
C. 12 (km)
D. $\frac{35}{3} (k m)$
Câu 435 : Cho hàm số y = f(x) liên tục và có đạo hàm trên $ℝ$ thỏa mãn $f (2) = - 2; \int_{0}^{2} f (x) d x = 1$ . Tính tích phân $I = \int_{0}^{4} f' (x) d x$

A. I = -10
B. I = -5
C. I = 0
D. I = -18
Câu 436 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy SA = $a \sqrt{2}$ . Gọi M, N lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SD (tham khảo hình vẽ). Góc giữa mặt phẳng (AMN) và đường thẳng SB bằng

A. 45 $°$
B. 60 $°$
C. 90 $°$
Câu 437 : Cho hàm số $f (x) = 3^{2 x} - 2 . 3^{x}$ có đồ thị như hình vẽ sau

A. 2
B. 4
C. 1
D. 3

Câu 438 : Trong không gian tọa độ Oxyz, cho đường thẳng $\frac{x - 1}{1} = \frac{y - 2}{- 2} = \frac{z + 1}{- 1}$ và mặt phẳng (P):2x - y - 2z - 2018 = 0. Phương trình mặt phẳng (Q) chứa đường thẳng D và tạo với (P) một góc nhỏ nhất cắt các trục tọa độ lần lượt tại các điểm A, B, C. Thể tích tứ diện O.ABC là:

A. $\frac{1}{6}$
B. $\frac{32}{3}$
C. $\frac{32}{6}$
D. $\frac{64}{3}$
Câu 439 : Cho hàm số y= f(x) xác định và có đạo hàm trên $ℝ$ thỏa mãn ${[f (1 + 2 x)]}^{2} = x - {[f (1 - x)]}^{3}$ . Viết phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ bằng 1.

A. $y = - \frac{1}{7} x - \frac{6}{7}$
B. $y = \frac{1}{7} x - \frac{8}{7}$
C. $y = - \frac{1}{7} x + \frac{8}{7}$
D. $y = - x + \frac{6}{7}$
Câu 440 : Gọi a là một nghiệm của phương trình $4 . 2^{2 \log x} - 6^{\log x} - 18 . 3^{2 \log x} = 0$ . Khẳng định nào sau đây đúng khi đánh giá về a.

A. ${(a - 10)}^{2} = 1$
B. a cũng là nghiệm của phương trình ${(\frac{2}{3})}^{\log x} = \frac{9}{4}$
C. $a^{2} + a + 1 = 2$
D. $a = 10^{2}$
Câu 441 : Cho hai điểm A(0;-1;2), B(4;1;-1) và mặt phẳng $(α) : 3 x - y + z - 2 = 0$ . Xét vị trí tương đối của hai điểm AB, và $(α)$ .

A. $A \notin (α), B \in (α)$
B. $A \in (α), B \notin (α)$
C. A, B nằm về một phía đối với $(α)$
D. A, B nằm về hai phía đối với $(α)$

Câu 442 : Cho f(x) là hàm số chẵn trên $ℝ$ thỏa mãn $\int_{- 3}^{0} f (x) d x = 2$ . Chọn mệnh đề đúng.

A. $\int_{- 3}^{3} f (x) d x = 2$
B. $\int_{- 3}^{3} f (x) d x = 4$
C. $\int_{0}^{3} f (x) d x = - 2$
D. $\int_{0}^{3} f (x) d x = - \int_{- 3}^{0} f (x) d x$
Câu 443 : Hàm số nào sau đây thỏa mãn với mọi $x_{1}, x_{2} \in ℝ, x_{1} > x_{2}$ thì $f (x_{1}) > f (x_{2})$ ?

A. $f (x) = x^{4} + 2 x^{2} + 1$
B. $f (x) = \frac{2 x + 1}{x + 3}$
C. $f (x) = x^{3} + x^{2} + 1$
D. $f (x) = x^{3} + x^{2} + 3 x + 1$
Câu 444 : Tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện $|z - (1 + i)| = |z + 2 i|$ là đường nào trong các đường cho dưới đây?

A. Đường thẳng
B. Đường tròn
C. Elip
D. Parabo
Câu 445 : Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số $y = f (x) = \sqrt{x} e^{x^{2}}$ , trục hoành, đường thẳng x = 1. Tính thể tích V của khối tròn xoay thu được khi (H) quay quanh trục hoành.

A. $V = e^{2} - 1$
B. $V = π (e^{2} - 1)$
C. $V = \frac{1}{4} π e^{2} - 1$
D. $V = \frac{1}{4} π (e^{2} - 1)$

Câu 446 : Tìm môđun của số phức $z = (- 4 + i \sqrt{48}) (2 + i)$

A. $8 \sqrt{5}$
B. $5 \sqrt{5}$
C. $6 \sqrt{5}$
D. $9 \sqrt{5}$
Câu 447 : Dạng lũy thừa với số mũ hữu tỉ của biểu thức $\frac{1}{8} \sqrt[7]{2^{5} a x^{3}}$ với a > 0, x > 0 là:

A. $2^{\frac{16}{7}} a^{- \frac{1}{7}} x^{\frac{3}{7}}$
B. $2^{\frac{16}{7}} a^{\frac{1}{7}} x^{- \frac{3}{7}}$
C. $2^{- \frac{16}{7}} a^{\frac{1}{7}} x^{\frac{3}{7}}$
D. $2^{\frac{16}{7}} a^{\frac{1}{7}} x^{\frac{3}{7}}$
Câu 448 : Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Số nghiệm của phương trình $2 |f (x) - 1| - 3 = 0$ là

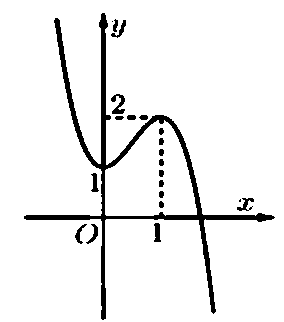
A. 1
B. 4
C. 3
D. 2
Câu 449 : Cho $x_{0}$ là nghiệm của phương trình $\sin x \cos x + 2 (\sin x + \cos x) = 2$ thì giá trị của biểu thức $P = \sin (x_{0} + \frac{π}{4})$ là

A. $P = \frac{\sqrt{2}}{2}$
B. P = 1
C. $P = \frac{1}{2}$
D. $P = - \frac{\sqrt{2}}{2}$

Câu 450 : Biết rằng x, y là các số thực thỏa mãn điều kiện $1 < x < \sqrt{y}$ . Tìm giá trị nhỏ nhất của biểu thức sau đây $P = {(\log_{x} y - 1)}^{2} + 8 {(\log_{\frac{\sqrt{y}}{x}} \frac{\sqrt{y}}{\sqrt{x}})}^{2}$

A. 18
B. 9
C. 27
D. 30
Câu 451 : Tổng các nghiệm của phương trình ${(\frac{z + i}{1 + i})}^{3} - \frac{z^{2} - 1 + 2 i z}{2 i} + 2 = 0$ là:

A. 1 + 2i
B. 2 - i
C. 1 - 2i
D. 2 + i
Câu 452 : Cho hàm số y = f(x) có đồ thị hàm số y = f '(x) như hình vẽ. Xét hàm số $g (x) = 2 f (x) + 2 x^{3} - 4 x - 3 m - 6 \sqrt{5}$ với m là số thực. Để $g (x) \leq 0, \forall x \in [- \sqrt{5}; \sqrt{5}]$ thì điều kiện của m là

A. $m \geq \frac{2}{3} f (\sqrt{5})$
B. $m \leq \frac{2}{3} f (\sqrt{5})$
C. $m \leq \frac{2}{3} f (0) - 2 \sqrt{5}$
D. $m \geq \frac{2}{3} f (- \sqrt{5}) - 4 \sqrt{5}$
Câu 453 : Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a, chiều cao bằng 2a. Mặt phẳng (P) qua B¢ và vuông góc AC¢ chia lăng trụ thành hai khối. Biết thể tích của hai khối là $V_{1}, V_{2}$ với $V_{1} < V_{2}$ . Tỉ số $\frac{V_{1}}{V_{2}}$ :

A. $\frac{1}{23}$
B. $\frac{1}{47}$
C. $\frac{1}{11}$
D. $\frac{1}{7}$

Câu 454 : Cho hai hộp đựng bi, đựng 2 loại bi là bi trắng và bi đen, tổng số bi trong hai hộp là 20 bi và hộp thứ nhất đựng ít hơn hộp thứ hai. Lấy ngẫu nhiên từ mỗi hộp 1 bi. Cho biết xác suất để lấy được 2 bi đen là $\frac{55}{84}$ . Tính xác suất để lấy được 2 bi trắng?

A. $\frac{15}{84}$
B. $\frac{1}{28}$
C. $\frac{11}{84}$
D. $\frac{11}{28}$
Câu 455 : Đồ thị của hàm số $y = 3 x^{4} - 4 x^{3} - 6 x^{2} + 12 x + 1$ đạt cực tiểu tại $M (x_{1}; y_{1})$ . Tính tổng $x_{1} + y_{1}$

A. 5
B. -11
C. 7
D. 6
Câu 456 : Cho hàm số y = f(x) có $\lim_{x \to - \infty} f (x) = 3$ và $\lim_{x \to - \infty} f (x) = - 3$ . Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số đã cho có đúng một tiện cận ngang
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 3 và x = -3
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 3 và y = -3
D. Đồ thị hàm số đã cho không có tiệm cận ngang
Câu 457 : Tập hợp các điểm trong mặt phẳng tọa đọ biễu diễn số phức z thỏa mãn điều kiện: $2 |2 - i| = |z - \bar{z} + 2 i|$ là hình gì?

A. Một đường thẳng.
B. Một đường Parabol
C. Một đường Elip
D. Một đường tròn

Câu 458 : Tìm tập nghiệm của bất phương trình $\log_{\frac{1}{2}} (x^{2} - 3 x + 2) \geq - 1$

A. $(- \infty; 1]$
B. $[0; 1) \cup (2; 3]$
C. $[0; 2) \cup (3; 7]$
D. [0;2)
Câu 459 : Cho số phức z = 3 -2i. Tìm phần ảo của số phức liên hợp của z?

A. 2i
B. -2i
C. 2
D. -2
Câu 460 : Biết F(x) là nguyên hàm của $f (x) = \frac{1}{x - 1}$ và F(2) = 1. Tính $F (3)$

A. ln2 + 1
B. $\frac{1}{2}$
C. $\ln \frac{3}{2}$
D. ln2
Câu 461 : Trong không gian với hệ tọa độ Oxyz, tính khoảng cách từ điểm M(1;2;-3) đến mặt phẳng (P):x + 2y - 2z - 2 = 0

A. 1
B. $\frac{11}{3}$
C. $\frac{1}{3}$
D. 3

Câu 462 : Trong không gian với hệ trục tọa độ Oxyz, tính góc giữa hai đường thẳng $d_{1} : \frac{x}{1} = \frac{y + 1}{- 1} = \frac{z - 1}{2}$ và $d_{2} : \frac{x + 1}{- 1} = \frac{y}{1} = \frac{z - 3}{1}$

A. 45 $°$
B. 30 $°$
C. 60 $°$
D. 90 $°$
Câu 463 : Biết rằng khi quay một đường tròn có bán kính bằng 1 quanh đường kính của nó thì ta được một mặt cầu. Tính diện tích mặt cầu đó.

A. $4 π$
B. $\frac{4}{3} π$
C. $2 π$
D. $π$
Câu 464 : Một người mỗi tháng gửi tiền đều đặn vào ngân hàng một khoản tiền T theo hình thức lãi kép với lãi suất 0,6% mỗi tháng. Biết sau 15 tháng người đó có số tiền là 10 triệu đồng. Hỏi số tiền T gần với số tiền nào nhất trong các số tiền sau đây?

A. 535.000
B. 635.000
C. 613.000
D. 643.000
Câu 465 : Trong không gian với hệ tọa độ Oxyz, cho điểm M(-3;2;4) gọi A, B, C lần lượt là hình chiếu của M trên Ox,Oy,Oz. Mặt phẳng nào sau đây song song với mặt phẳng (ABC)?

A. 4x - 6y - 3z + 12 = 0
B. 3x - 6y - 4z + 12 = 0
C. 4x - 6y - 3z - 12 = 0
D. 6x - 4y - 3z - 12 = 0

Câu 466 : Một vật chuyển động với vận tốc 10 (m/s) thì tăng tốc với gia tốc $3 t + t^{2}, (m / s^{2})$ . Quảng đường vật di chuyển trong thời gian 10 giây kể từ lúc bắt đầu tăng tốc

A. 3600 m
B. $\frac{4300}{3}$ m
C. $\frac{1750}{3}$ m
D. $\frac{1450}{3}$ m
Câu 467 : Cho tam giác AOB vuông tại O và OAB = 30 $°$ . Đường cao hạ từ O là OH, OH = a. Tính thể tích khối nón tròn xoay tạo bởi tam giác AOB khi quay quanh trục OA.

A. $\frac{π}{3} a^{3}$
B. $\frac{9}{10} π a^{3}$
C. $\frac{9}{8} π a^{3}$
D. $\frac{8}{9} π a^{3}$
Câu 468 : Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d có phương trình $\frac{x - 1}{2} = \frac{y}{- 5} = \frac{z - 3}{4} .$ Viết phương trình mặt phẳng $(α)$ chứa trục Oy và song song với đường thẳng d

A. -2x + y = 0
B. x - 2z = 0
C. 2x - z = 0
D. 2x + z = 0
Câu 469 : Tìm tập xác định D của hàm số $y = \log (\frac{x - 2}{1 - x})$

A. $D = (- \infty; 1) \cup (2; + \infty)$
B. $D = (1; 2)$
C. $D = ℝ \ \{1\}$
D. $D = ℝ \ (1; 2)$

Câu 470 : Tìm công thức tính thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi parabol (P): y = $x^{2}$ và đường thẳng d: y = 2x quay xung quanh trục Ox

A. $π \int_{0}^{2} {(x^{2} - 2 x)}^{2} d x$
B. $π \int_{0}^{2} 4 x^{2} d x - π \int_{0}^{2} x^{4} d x$
C. $π \int_{0}^{2} 4 x^{2} d x + π \int_{0}^{2} x^{4} d x$
D. $π \int_{0}^{2} {(2 x - x^{2})}^{2} d x$
Câu 471 : Đồ thị các hàm số $y = \frac{4 x + 4}{x - 1}$ và $y = x^{2} - 1$ cắt nhau tại bao nhiêu điểm?

A. 0
B. 1
C. 2
D. 3
Câu 472 : Tính môđun số phức nghịch đảo của số phức $z = {(1 - 2 i)}^{2}$

A. $\frac{1}{\sqrt{5}}$
B. $\sqrt{5}$
C. $\frac{1}{25}$
D. $\frac{1}{5}$
Câu 473 : Trong không gian với hệ trục tọa độ Oxyz, tính khoảng cách từ điểm M(1;3;2) đến đường thẳng có phương trình $(d) : \{\begin{cases} x = 1 + t \\ y = 1 + t \\ z = - t \end{cases}$

A. $\sqrt{2}$
B. 2
C. $2 \sqrt{2}$
D. 3

Câu 474 : Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình $\{\begin{cases} x = 6 + t \\ y = - 2 - 5 t \\ z = - 1 + t \end{cases}$ . Xét đường thẳng $∆ : \frac{x - a}{5} = \frac{y - 1}{- 12} = \frac{z + 5}{- 1}$ , với a là tham số thực. Tìm tất cả các giá trị của a để đường thẳng d và $∆$ cắt nhau.

A. a = 0
B. a = 4
C. a = 8
D. $a = \frac{1}{2}$
Câu 475 : Xét hàm số $y = f (x) = 2 x^{4} - 3 x^{2} + m$ liên tục trên $[- \frac{1}{2}; 2] .$ Tìm tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số trên đoạn đã cho bằng $\frac{31}{8}$

A. m = -4
B. m = $\pm 3$
C. m = 2
D. m = 5
Câu 476 : Có bao nhiêu giá trị m để đồ thị hàm số $y = \frac{m x^{2} - 1}{x^{2} - 3 x + 2}$ có đúng 2 đường tiệm cận?

A. 2
B. $\forall m$
C. 3
D. 1
Câu 477 : Tính tổng diện tích tất cả các mặt của khối đa diện đều loại {3;5} có cạnh bằng 1

A. $\frac{5 \sqrt{3}}{2}$
B. $5 \sqrt{3}$
C. $3 \sqrt{3}$
D. $\frac{3 \sqrt{3}}{2}$

Câu 478 : Cho hàm số $f (x) = \frac{4^{x}}{4^{x} + 2}$ . Hãy tính giá trị của tổng sau:

A. $\frac{1007}{2}$
B. $\frac{3025}{6}$
C. $\frac{1511}{3}$
D. $504$
Câu 479 : Biết rằng chỉ có hai giá trị thực khác nhau của tham số m thì đồ thị hàm số $y = \frac{m + 1}{x^{2} - 2 x + m}$ có đúng hai đường tiệm cận; kí hiệu m = a là giá trị thứ nhất, m = a là giá trị thứ hai. Tính ab

A. ab = -1
B. ab = -2
C. ab = -3
D. ab = -4
Câu 480 : Gọi $T = [a; b]$ là tập các giá trị của hàm số $y = \frac{x + 1}{\sqrt{x^{2} + 1}}$ trên [-1;2]. Khẳng định nào sau đây là đúng?

A. $a^{2} + b^{2} = \sqrt{2}$
B. $a^{2} + b^{2} = \frac{9}{5}$
C. $a^{2} + b^{2} = \frac{19}{5}$
D. $a^{2} + b^{2} = 2$
Câu 481 : Biết rằng T=[a;b] là tập tất cả các giá trị thực của tham số m để phương trình $\log_{\frac{1}{3}}^{2} x + \sqrt{\log_{3}^{2} + 1} - 1 - 5 m = 0$ có ít nhất một nghiệm thuộc khoảng $[1; 3^{2 \sqrt{2}}]$ . Tính $a^{2} + b^{2}$

A. $a^{2} + b^{2} = 4$
B. $a^{2} + b^{2} = 6$
C. $a^{2} + b^{2} = 8$
D. $a^{2} + b^{2} = 10$

Câu 482 : Tính tích phân $\int_{1}^{e} \frac{x^{2} + \ln x}{x^{3}} d x = \frac{a}{b} - \frac{3}{4 e^{2}}$ , trong đó a, b dương và $\frac{a}{b}$ là phân số tối giản. Tính ab

A. ab = 10
B. ab = 20
C. ab = 40
D. ab = 30
Câu 483 : Cho số phức z thỏa mãn điều kiện $|z| = 1$ . Tìm giá trị lớn nhất của $A = |1 + z| + 3 |1 - z|$

A. $4 \sqrt{8}$
B. $2 \sqrt{15}$
C. $\sqrt{10}$
D. $2 \sqrt{10}$
Câu 484 : Cho khối tứ diện ABCD có thể tích V. Gọi $G_{1}, G_{2}, G_{3}, G_{4}$ là trọng tâm 4 mặt của tứ diện ABCD. Thể tích của khối tứ diện $G_{1} G_{2} G_{3} G_{4}$ là

A. $\frac{V}{27}$
B. $\frac{V}{18}$
C. $\frac{V}{4}$
D. $\frac{V}{12}$
Câu 485 : Cho hình thang cân ABCD có các cạnh đáy AB = 2a, CD = 4a và cạnh bên AD = BC = 3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.

A. $V = \frac{4}{3} {πa}^{3}$
B. $V = \frac{4 + 10 \sqrt{2}}{3} {πa}^{3}$
C. $V = \frac{10 \sqrt{2}}{3} {πa}^{3}$
D. $V = \frac{14 \sqrt{2}}{3} {πa}^{3}$

Câu 486 : Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để điểm cực tiểu của đồ thị hàm số $y = x^{3} + x^{2} + m x - 1$ nằm bên phải trục tung. Tìm số phần tử của tập hợp $(- 5; 6) \cap S$

A. 2
B. 5
C. 3
D. 4
Câu 487 : Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) chứa đường thẳng $d : \frac{x - 1}{2} = \frac{y}{1} = \frac{z + 1}{3}$ và vuông góc với mặt phẳng (Q):2x + y - z = 0

A. x + 2y + z = 0
B. x - 2y - 1 = 0
C. x + 2y - 1 = 0
D. x - 2y + z = 0
Câu 488 : Một chậu nước hình trụ cao 12 cm, rộng 10 cm. Người ta đổ nước vào trong chậu sao cho nước trong chậu cao 10 cm. Sau đó người ta thả các viên bi vào chậu, biết bán kính mỗi viên bi là 2 cm và sau mỗi lần thả viên bi vào thì nước bắn ra ngoài bằng 15% thể tích viên bi. Hỏi cần thả ít nhất bao nhiêu viên bi vào chậu nước thì nước vừa bắn vừa đầy miệng chậu tràn ra ngoài

A. 4
B. 5
C. 6
D. 7
Câu 489 : Một vật chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc tính theo thời gian t là $a (t) = 3 t + t^{2}$ . Tính quãng đường vật đi được trong khoảng 10s kể từ khi bắt đầu tăng tốc.

A. $\frac{3400}{3} k m$
B. $\frac{4300}{3} k m$
C. $\frac{130}{3} k m$
D. $130 k m$

Câu 490 : Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x + 6 y - 4 z - 2 = 0$ mặt phẳng $(α) : x + 4 y + z - 11 = 0$ . Gọi (P) là mặt phẳng vuông góc với (a), (P) song song với giá của véctơ $\vec{v} = (1; 6; 2)$ và (P) tiếp xúc với (S). Lập phương trình mặt phẳng (P).

A. 2x - y + 2z - 2 = 0 và x - 2y + z - 21 = 0
B. x - 2y + 2z + 3 = 0 và x - 2y + z - 21 = 0
C. 2x - y + 2z + 3 = 0 và 2x - y + 2z - 21 = 0
D. 2x - y + 2z + 5 = 0 và 2x - y + 2z - 2 = 0
Câu 491 : Bạn Linh cần mua một chiếc gương hình dạng đường Parabol bậc 2 (xem hình vẽ).

A. $1000 (c m^{2})$
B. $1200 (c m^{2})$
C. $1400 (c m^{2})$
D. $900 (c m^{2})$
Câu 492 : Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) trong đó a > 0, b > 0, c > 0. Mặt phẳng (ABC) đi qua điểm I(1;2;3) sao cho thể tích khối tứ diện OABC đạt giá trị nhỏ nhất. Chọn đẳng thức không đúng khi nói về a, b, c?

A. a + b + c = 12
B. $a^{2} + b = c + 6$
C. a + b + c = 18
D. a + b - c = 0
Câu 493 : Biết $\int_{0}^{2} 2 x \ln (x + 1) d x = a \ln b$ với $a, b \in ℕ *$ và b là số nguyên tố. Tính 6a + 7b.

A. 33
B. 25
C. 42
D. 39

Câu 494 : Cho n là số nguyên dương thỏa mãn $A_{n}^{2} = C_{n}^{2} + C_{n}^{1} + 4 n + 6$ . Hệ số của số hạng chứa $x^{9}$ của khai triển biểu thức $P (x) = {(x^{2} + \frac{3}{x})}^{n}$ bằng:

A. 18564
B. 64152
C. 192456
D. 194256
Câu 495 : Cho $\log_{2} 5 = a$ và $\log_{5} 3 = b$ . Tính $\log_{24} 15$ theo a và b?

A. $\frac{a (1 + b)}{a b + 3}$
B. $\frac{a (1 + 2 b)}{a b + 1}$
C. $\frac{a (1 + 2 b)}{a b + 3}$
D. $\frac{a}{a b + 1}$
Câu 496 : Cho $z_{1}, z_{2}$ là hai nghiệm của phương trình $2017 z^{2} - 2016 z + 2017 = 0$ . Tính giá trị của biểu thức $P = {|1 - \vec{z_{1}} . z_{2}|}^{2} - {|z_{1} - z_{2}|}^{2}$

A. 3
B. $\frac{1}{3}$
C. 1
D. 6
Câu 497 : Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng (P):3x - 2y + 2z - 5 = 0 và (Q):4x + 5y - z + 1 = 0. Các điểm A, B phân biệt thuộc giao tuyến của hai mặt phẳng (P) và (Q). Véctơ $\vec{A B}$ cùng phương với vecto nào sau đây?

A. $\vec{w} = (3; - 2; 2)$
B. $\vec{v} = (- 8; 11; - 23)$
C. $\vec{a} = (4; 5; - 1)$
D. $\vec{u} = (8; - 11; - 23)$

Câu 498 : Cho hình nón có độ dài đường kính đáy là 2R, độ dài đường sinh là $R \sqrt{17}$ và hình trụ có chiều cao và đường kính đáy đều bằng 2R, lồng vào nhau như hình vẽ bên. Tính thể tích phần khối trụ không giao với khối nón

A. $\frac{5}{12} {πR}^{3}$
B. $\frac{1}{3} {πR}^{3}$
C. $\frac{4}{3} {πR}^{3}$
D. $\frac{5}{6} {πR}^{3}$
Câu 499 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh SA = a, vuông góc với mặt phẳng (ABCD) và SA = $a \sqrt{6}$ . Gọi a là góc giữa đường thẳng SB và mặt phẳng (SAC). Tính $\sin α$ ta được kết quả là

A. $\frac{1}{\sqrt{14}}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{\sqrt{3}}{2}$
D. $\frac{1}{5}$
Câu 500 : Cho hàm số $y = \sqrt{1 + 3 x - x^{2}}$ . Khẳng định nào dưới đây đúng?

A. ${(y')}^{2} + y . y'' = - 1$
B. ${(y')}^{2} + 2 y . y'' = 1$
C. $y . y'' - {(y')}^{2} = 1$
D. ${(y')}^{2} + y . y'' = 1$
Câu 501 : Cho hình phẳng (H) giới hạn bởi đường cong $y = \frac{\ln x}{\sqrt{x}}$ , trục hoành và đường thẳng x = e. Khối tròn xoay tạo thành khi quay (H) quanh trục hoành có thể tích V bằng bao nhiêu?

A. $V = \frac{π}{2}$
B. $V = \frac{π}{3}$
C. $V = \frac{π}{6}$
D. $V = π$

Câu 502 : Tìm tất cả các giá trị thực của m để phương trình $x + 1 = m \sqrt{2 x^{2} + 1}$ có hai nghiệm phân biệt?

A. $- \frac{\sqrt{2}}{2} < m < \frac{\sqrt{6}}{6}$
B. $m < \frac{\sqrt{2}}{2}$
D. $m > \frac{\sqrt{6}}{6}$
D. $\frac{\sqrt{2}}{2} < m < \frac{\sqrt{6}}{6}$
Câu 503 : Tìm giá trị nguyên của tham số m để hàm số $y = x^{4} - 2 (m^{2} + 1) x^{2} + 2$ có ba điểm cực trị sao cho giá trị cực tiểu đạt giá trị lớn nhất.

A. m = 2
B. m = 0
C. m = 1
D. m = 2
Câu 504 : Gọi (H) là hình phẳng giới hạn bởi đồ thị (P) của hàm số $y = 6 x - x^{2}$ và trục hoành. Hai đường thẳng $y = m, y = n$ chia hình (H) thành ba phần có diện tích bằng nhau. Tính $P = {(9 - m)}^{3} + {(9 - n)}^{3}$

A. P = 405
B. P = 409
C. P = 407
D. P = 403
Câu 505 : Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x + y - 2z + m = 0 và mặt cầu (S) có phương trình $x^{2} + y^{2} + z^{2} - 2 x + 4 y - 6 z - 2 = 0$ . Có bao nhiêu giá trị nguyên của m để mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (T) có chu vi bằng $4 π \sqrt{3}$ .

A. 3
B. 4
C. 2
D. 1

Câu 506 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, góc giữa hai mặt phẳng (SBC) và (ABCD) bằng $30 °$ . Tính tỉ số $\frac{3 V}{a^{3}}$ biết V là thể tích của khối chóp S.ABCD?

A. $\frac{\sqrt{3}}{12}$
B. $\frac{\sqrt{3}}{12}$
C. $\sqrt{3}$ 3
D. $\frac{8 \sqrt{3}}{3}$
Câu 507 : Với giá trị lớn nhất của a bằng bao nhiêu để phương trình $a \sin^{2} x + 2 \sin 2 x + 3 a \cos^{2} x = 2$ có nghiệm?

A. 2
B. $\frac{11}{3}$
C. 4
D. $\frac{8}{3}$
Câu 508 : Cho hàm số y = f(x) liên tục trên $ℝ$ và có đồ thị như hình dưới. Biết rằng trục hoành là tiệm cận ngang của đồ thị. Tìm tất cả các giá trị thực của tham số m để phương trình $f (x) = 4^{m + 2 \log_{4} \sqrt{2}}$ có hai nghiệm phân biệt dương.

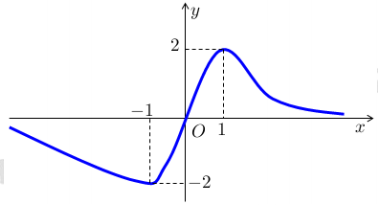
A. m > 1
B. 0 < m < 1
C. m < 0
D. 0 < m < 2
Câu 509 : Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x - y + z - 10 = 0 điểm A(1;3;2) và đường thẳng $d : \{\begin{cases} x = - 2 + 2 t \\ y = 1 + t \\ z = 1 - t \end{cases}$ . Tìm phương trình đường thẳng D cắt (P) và d lần lượt tại hai điểm M và N sao cho A là trung điểm của cạnh MN

A. $\frac{x - 6}{7} = \frac{y - 1}{- 4} = \frac{z + 3}{- 1}$
B. $\frac{x + 6}{7} = \frac{y + 1}{4} = \frac{z - 3}{- 1}$
C. $\frac{x - 6}{7} = \frac{y - 1}{4} = \frac{z + 3}{- 1}$
D. $\frac{x + 6}{7} = \frac{y + 1}{- 4} = \frac{z - 3}{- 1}$

Câu 510 : Giả sử a, b, c là các số nguyên thỏa mãn $\int_{0}^{4} \frac{2 x^{2} + 4 x + 1}{\sqrt{2 x + 1}} d x = \frac{1}{2} \int_{1}^{3} (a u^{4} + b u^{2} + c) d u$ , trong đó $u = \sqrt{2 x + 1}$ . Tính giá trị của S = a + b + c

A. S = 3
B. S = 0
C. S = 1
D. S = 2
Câu 511 : Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0;1;0), B(2;2;2), C(-2;3;1) và đường thẳng $d : \frac{x - 1}{2} = \frac{y + 2}{- 1} = \frac{z - 3}{2}$ . Tìm điểm M thuộc d để thể tích V của tứ diện MABC bằng 3.

A. $M_{1} (- \frac{15}{2}; \frac{9}{4}; - \frac{11}{2}), M_{2} (- \frac{3}{2}; - \frac{3}{4}; \frac{1}{2})$
B. $M_{1} (- \frac{3}{5}; - \frac{3}{4}; \frac{1}{2}), M_{2} (- \frac{15}{2}; \frac{9}{4}; \frac{11}{2})$
C. $M_{1} (\frac{3}{2}; - \frac{3}{4}; \frac{1}{2}), M_{2} (\frac{15}{2}; \frac{9}{4}; \frac{11}{2})$
D. $M_{1} (\frac{3}{5}; - \frac{3}{4}; \frac{1}{2}), M_{2} (\frac{15}{2}; \frac{9}{4}; \frac{11}{2})$
Câu 512 : Cho hình lập phương ABCD. A’B’C’D’ có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A’B’C’D’. Kết quả tính diện tích toàn phần $S_{t p}$ của hình nón đó có dạng bằng $\frac{{πa}^{2}}{4} (\sqrt{b} + c)$ với b, c là hai số nguyên dương và b > 1. Tính giá trị của bc?

A. bc = 5
B. bc = 8
C. bc = 15
D. bc = 7
Câu 513 : Tập nghiệm của bất phương trình $2 . 7^{x + 2} + 7 . 2^{x + 2} \leq 351 \sqrt{14^{x}}$ có dạng S = [a;b]. Giá trị b - 2a thuộc khoảng nào sau đây?

A. $(3; \sqrt{10})$
B. (-4;2)
C. $(\sqrt{7}; 4 \sqrt{10})$
D. $(\frac{2}{9}; \frac{49}{5})$

Câu 514 : Cho dãy số $(U_{n})$ xác định bởi $U_{1} = \frac{1}{3}$ và $U_{n + 1} = \frac{n + 1}{3 n} U_{n}$ . Tổng $S = U_{1} + \frac{U_{2}}{2} + \frac{U_{3}}{3} + . . . + \frac{U_{10}}{10}$ bằng

A. $\frac{3280}{6561}$
B. $\frac{29524}{59049}$
C. $\frac{25942}{59049}$
D. $\frac{1}{243}$
Câu 515 : Cho hàm số f(x) có đạo hàm $f' (x) = {(x + 1)}^{4} {(x - 2)}^{5} {(x + 3)}^{3}$ . Số điểm cực trị của hàm số $f (|x|)$ là

A. 5
B. 3
C. 1
D. 2
Câu 516 : Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;0;0), B(0;2;0), C(0;0;3), D(2;-2;0). Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 trong 5 điểm O, A, B, C, D

A. 7
B. 5
C. 6
D. 10
Câu 517 : Cho bất phương trình $1 + \log_{5} (x^{2} + 1) \geq \log_{5} (m x^{2} + 4 x + m)$ (1). Tìm tất cả các giá trị của m để (1) nghiệm đúng với mọi số thực x.

A. $2 \leq m \leq 3$
B. $2 < m \leq 3$
C. $- 3 \leq m \leq 7$
D. $[\begin{array}{l} m \leq 3 \\ m \geq 7 \end{array}$

Câu 518 : Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 16$ và các điểm A(1;0;2), B(-1;2;2). Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) và mặt cầu (S ) có diện tích nhỏ nhất. Khi đó viết phương trình (P):ax + by + cz + 3 = 0. Tính giá trị của T = a + b + c.

A. 3
B. -3
C. 0
D. -2
Câu 519 : Có bao nhiêu giá trị nguyên của tham số m để phương trình $\sqrt{1 + 2 \cos x} + \sqrt{1 + 2 \sin x} = \frac{m}{2}$ có nghiệm thực?

A. 3
B. 5
C. 4
D. 2
Câu 520 : Biết rằng đồ thị hàm số $y = f (t) = a x^{4} + b x^{3} + c x^{2} + d x + e, (a, b, c, d \in ℝ; a \neq 0, b \neq 0)$ cắt trục hoành Ox tại 4 điểm phân biệt. Khi đó đồ thị hàm số $y = g (x) = {(4 a x^{3} + 3 b x^{2} + 2 c x + d)}^{2} - 2 (6 a x^{2} + 3 b x + c) . (a x^{4} + b x^{3} + c x^{2} + d x + e)$ cắt trục hoành Ox tại bao nhiêu điểm?

A. 6
B. 0
C. 4
D. 2
Câu 521 : An và Bình cùng tham gia kỳ thi THPTQG năm 2018, ngoài thi ba môn Toán, Văn, Tiếng Anh bắt buộc thì An và Bình đều đăng ký thi thêm đúng hai môn tự chọn khác trong ba môn Vật lý, Hóa học và Sinh học dưới hình thức thi trắc nghiệm để xét tuyển Đại học. Mỗi môn tự chọn trắc nghiệm có 8 mã đề thi khác nhau, mã đề thi của các môn khác nhau là khác nhau. Tìm xác suất để An và Bình có chung đúng một môn thi tự chọn và chung một mã đề?

A. $\frac{1}{9}$
B. $\frac{1}{10}$
C. $\frac{1}{12}$
D. $\frac{1}{24}$

Câu 522 : Xét tứ diện OABC có OA, OB, OC đôi một vuông góc nhau. Gọi $α, β, γ$ lần lượt là góc giữa các đường thẳng OA, OB, OC với mặt phẳng (ABC). Khi đó giá trị nhỏ nhất của biểu thức $M = (3 + c o t^{2} α) (3 + c o t^{2} β) (3 + c o t^{2} γ)$

A. Số khác
B. $48 \sqrt{3}$
C. 48
D. 125
Câu 523 : Biết luôn có hai số a và b để $F (x) = \frac{a x + b}{x + 4} (4 a - b \neq 0)$ là nguyên hàm của hàm số f(x) thỏa mãn $2 f^{2} (x) = [F (x) - 1] . f' (x)$ . Khẳng định nào sau đây đúng và đầy đủ nhất?

A. a = 1,b = 4
B. a = 1,b = -1
C. $a = 1, b \in ℝ \ \{4\}$
D. $a \in ℝ, b \in ℝ$
Câu 524 : Cho cấp số nhân $(b_{n})$ thỏa $b_{2} > b_{1} \geq 1$ , hàm $f (x) = x^{3} - 3 x$ thỏa $f [\log_{2} (b_{2})] + 2 = f [\log_{2} (b_{1})]$ . Giá trị nhỏ nhất của n để $b_{n} > 5^{100}$

A. 234
B. 229
C. 333
D. 292
Câu 525 : Cho dãy số $(u_{n})$ xác định bởi $u_{1} = 0$ và $u_{n + 1} = u_{n} + 4 n + 3$ với $\forall n \geq 2$ . Biết rằng dãy số thỏa mãn $l i m \frac{\sqrt{u_{n}} + \sqrt{u_{4 n}} + \sqrt{u_{4^{2} n}} + . . . + \sqrt{u_{4^{2018} n}}}{\sqrt{u_{n}} + \sqrt{u_{2 n}} + \sqrt{u_{2^{2} n}} + . . . + \sqrt{u_{2^{2018} n}}} = \frac{a^{2019} + b}{c}$ với a, b, c là các số nguyên dương và b < 2019. Tính giá trị của S = a + b - c

A. S = -1
B. S = 0
C. S = 2017
D. S = 2018

Câu 526 : Cho hai số phức $z_{1}; z_{2}$ thỏa mãn $|z_{1} + 1 - i| = 2$ và $z_{1} = z_{2}$ . Tìm giá trị nhỏ nhất m của biểu thức $|z_{1} - z_{2}|$

A. $m = \sqrt{2} - 1$
B. $m = 2 \sqrt{2}$
C. $m = 2$
D. $m = 2 \sqrt{2} - 2$
Câu 527 : Cho y = f(x) là hàm số chẵn, liên tục trên biết đồ thị hàm số y = f(x) đi qua điểm

A. I = 10
B. I = -2
C. I = 1
D. I = -1
Câu 528 : Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam giác trung bình của tam giác ABC. Ta xây dựng dãy các tam giác $A_{1} B_{1} C_{1}, A_{2} B_{2} C_{2}, A_{3} B_{3} C_{3}, . . .$ sao cho $A_{1} B_{1} C_{1}$ là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương $n \geq 2$ , tam giác $A_{n} B_{n} C_{n}$ là tam giác trung bình của tam giác $A_{n - 1} B_{n - 1} C_{n - 1}$ . Với mỗi số nguyên dương n, kí hiệu n S tương ứng là diện tích hình tròn ngoại tiếp tam giác $A_{n} B_{n} C_{n}$ . Tính tổng $S = S_{1} + S_{2} + . . . + S_{n} + . . . ?$

A. $S = \frac{15 π}{4}$
B. $S = 4 π$
C. $S = \frac{9 π}{2}$
D. $S = 5 π$
Câu 529 : Cho ab, là các số thực dương thỏa mãn $\frac{1}{2} \log_{2} a = \log_{2} \frac{2}{b}$ . Hỏi giá trị nhỏ nhất của biểu thức sau $P = 4 a^{3} + b^{3} - 4 \log_{2} (4 a^{3} + b^{3})$ là:

A. -4
B. $4 \log_{2} 6$
C. $\frac{4}{\ln 2} - 4 \log_{2} (\frac{4}{\ln 2})$
D. $4 (1 - \log_{2} 3)$

Câu 530 : Cho x, y là các số thực dương thỏa mãn $\log_{25} \frac{x}{2} = \log_{15} y = \log_{9} \frac{x + y}{4}$ và $\frac{x}{y} = \frac{- a + \sqrt{b}}{2}$ với a, b là các số nguyên dương. Tính a + b

A. 14
B. 3
C. 21
D. 32
Câu 531 : Tính tổng tất cả các nghiệm của phương trình $e^{\sin (x - \frac{π}{4})} = \tan x$ thuộc đoạn $(0; 50 π)$ ?

A. $\frac{1853 π}{2}$
B. $\frac{2475 π}{2}$
C. $\frac{2671 π}{2}$
D. $\frac{2105 π}{2}$
Câu 532 : Cho phương trình $2 \log_{4} (2 x^{2} - x + 2 m - 4 m^{2}) + \log_{\frac{1}{2}} (x^{2} + m x - 2 m^{2}) = 0$ . Biết rằng $S = (a; b) \cup (c; d), a < b < c < d$ là tập hợp các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt $x_{1}, x_{2}$ thỏa ${x_{1}}^{2} + {x_{2}}^{2} > 1$ . Tính giá trị biểu thức A = a + b + 5c + 2d

A. A = 1
B. A = 2
C. A = 0
D. A = 3
Câu 533 : Gia đình Thầy Hùng ĐZ xây một bể nước dạng hình hộp chữ nhật có nắp dung tích 2018 lít, đáy bể là một hình chữ nhật có chiều dài gấp ba lần chiều rộng được làm bằng bê tông có giá 250.000 đồng/m², thân bể được xây bằng gạch có giá 200.000 đồng/m²và nắp bể làm bằng tôn có giá 100.000 đồng/m². Hỏi chi phí thấp nhất gia đình Thầy cần bỏ ra để xây dựng bể nước là bao nhiêu? (làm tròn đến hàng đơn vị)

A. 2.017.332 đồng
B. 2.017.331 đồng
C. 2.017.333 đồng
D. 2.017.334 đồng

Câu 534 : Một bạn đã cắt tấm bìa carton phẳng và cứng có kích thước như hình vẽ. Sau đó bạn ấy gấp theo đường nét đứt thành một hình hộp chữ nhật. Hình hộp có đáy là hình vuông cạnh a (cm), chiều cao là h (cm) và diện tích tấm bìa là $3 m^{2}$ . Tổng a + h bằng bao nhiêu để thể tích hộp là lớn nhất

A. $2 \sqrt{2}$
B. $\frac{\sqrt{2}}{2}$
C. 46,3
D. $\sqrt{2}$
Câu 535 : Cho hàm số $y = x^{3} - \frac{3}{4} x^{2} - \frac{3}{2} x$ có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m sao cho phương trình $4 |x^{3}| - 3 x^{2} - 6 |x| = m^{2} - 6 m$ có đúng ba nghiệm phân biệt

A. m = 0 hoặc m = 6
B. m < 0 hoặc m > 6
C. 0 < m < 3
D. 1 < m < 6
Câu 536 : Cho hình lập phương cạnh 4cm. Trong khối lập phương là khối cầu tiếp xúc với các mặt của hình lập phương. Tính thể tích phần còn lại của khối lập phương.

A. $64 - \frac{64 \sqrt{2}}{3} π {cm}^{3}$
B. $64 - 32 \sqrt{3} π {cm}^{3}$
C. $64 - \frac{32}{3} π {cm}^{3}$
D. $64 - \frac{256}{81} π {cm}^{3}$
Câu 537 : Tìm nguyên hàm của hàm số $f (x) = \cos^{2} x$ ta được

A. $\int f (x) d x = \frac{x}{2} - \frac{\cos 2 x}{4} + C$
B. $\int f (x) d x = \frac{x}{2} - \frac{\sin 2 x}{4} + C$
C. $\int f (x) d x = \frac{x}{2} + \frac{\cos 2 x}{4} + C$
D. $\int f (x) d x = \frac{x}{2} + \frac{\sin 2 x}{4} + C$

Câu 538 : Cho phương trình $\cos 2 (x + \frac{π}{3}) + 4 \cos (\frac{π}{6} - x) = \frac{5}{2}$ . Khi đặt $t = \cos (\frac{π}{6} - x)$ , phương trình đã cho trở thành phương trình nào dưới đây?

A. $4 t^{2} - 8 t + 3 = 0$
B. $4 t^{2} - 8 t - 3 = 0$
C. $4 t^{2} + 8 t - 5 = 0$
D. $4 t^{2} - 8 t + 5 = 0$
Câu 539 : Trong các hàm số dưới đây, hàm số nào không nghịch biến trên $ℝ$ ?

A. $y = - x^{3} + 2 x^{2} - 7 x$
B. $y = - 4 x + \cos x$
C. $y = - \frac{1}{x^{2} + 1}$
D. $y = {(\frac{\sqrt{2}}{\sqrt{2} + \sqrt{3}})}^{x}$
Câu 540 : Cho đường thẳng $d : \frac{x + 1}{2} = \frac{y - 4}{- 2} = \frac{z + 2}{1}$ và mặt phẳng $(P) : x + 2 y - z - 6 = 0$ cắt nhau tại I. Gọi M là điểm thuộc d sao cho IM = 6. Tính khoảng cách từ điểm M đến mặt phẳng (P).

A. $\sqrt{6}$
B. $2 \sqrt{6}$
C. $\sqrt{30}$
D. $\frac{\sqrt{6}}{2}$
Câu 541 : Kí hiệu $z_{0}$ là nghiệm phức có phần thực âm và phần ảo dương của phương trình $z^{2} + 2 z + 10 = 0$ . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức $w = i^{2017} z_{0}$ ?

A. M(3;-1)
B. M(3;1)
C. M(-3;1)
D. M(-3;-1)

Câu 542 : Tính tổng S các nghiệm của phương trình $(2 \cos 2 x + 5) (\sin^{4} x - \cos^{4} x) + 3 = 0$ trong khoảng $(0; 2 π)$ .

A. $S = \frac{11 π}{6}$
B. $S = 4 π$
C. $S = 5 π$
D. $S = \frac{7 π}{6}$
Câu 543 : Biết rằng phương trình ${(x - 2)}^{\log_{2} [4 (x - 2)]} = 4 . {(x - 2)}^{3}$ có hai nghiệm $x_{1}, x_{2} (x_{1} < x_{2})$ . Tính $2 x_{1} - x_{2}$ .

A. 1
B. 3
C. -5
D. -1
Câu 544 : Viết phương trình mặt phẳng vuông góc với mặt phẳng $(α) : 2 x - 3 y + z - 2 = 0$ và chứa đường thẳng $d : \frac{x}{- 1} = \frac{y + 1}{2} = \frac{z - 2}{- 1} .$

A. x - y + z - 3 = 0
B. 2x + y - z + 3 = 0
C. x + y + z - 1 = 0
D. 3x + y - z + 3 = 0
Câu 545 : Tìm số phức liên hợp của số phức $z = (1 - i) (3 + 2 i)$ .

A. $z = 1 + i$
B. $z = 5 + i$
C. $z = 5 - i$
D. $z = 1 - i$

Câu 546 : Tìm số nghiệm thuộc $[- \frac{3 π}{2}; - π)$ của phương trình $\sqrt{3} \sin x = \cos (\frac{3 π}{2} - 2 x)$ .

A. 0
B. 1
C. 2
D. 3
Câu 547 : Cho hàm số $y = a x^{4} + b x^{2} + c$ có đồ thị là hình vẽ dưới đây. Mệnh đề nào sau đây là đúng?

A. $a > 0, b < 0, c > 0, b^{2} - 4 a c > 0$
B. $a > 0, b < 0, c > 0, b^{2} - 8 a c > 0$
C. $a > 0, b < 0, c > 0, b^{2} - 4 a c < 0$
D. $a > 0, b < 0, c > 0, b^{2} - 8 a c < 0$
Câu 548 : Cho khối lăng trụ ABC.A’B’C’ có đáy làm tam giác vuông tại B, AB = a, BC = 2a và có thể tích bằng $2 a^{2}$ . Tính khoảng cách giữa hai đáy lăng trụ.

A. 6a
B. a
C. 2a
D. 3a
Câu 549 : Cho đường thẳng $d : \frac{x - 1}{- 1} = \frac{y}{2} = \frac{z - 3}{4}$ và mặt phẳng (P): 2x - y + z - 5 = 0. Xét vị trí tương đối của (d) và (P).

A. d nằm trên (P)
B. d song song với (P)
C. d cắt và vuông góc với (P)
D. d vuông góc với (P)

Câu 550 : Biết $\int_{a}^{b} f (x) d x = 10, \int_{a}^{b} g (x) d x = 5 .$ Tính $I = \int_{a}^{b} (3 f (x) - 5 g (x)) d x$ .

A. I = -5
B. I = 15
C. I = 5
D. I = 10
Câu 551 : Cho hình chóp đều SABC có AB = 1cm, SA = 2cm. Tính diện tích xung quanh $S_{x q}$ của hình nón ngoại tiếp hình chóp SABC.

A. $S_{x q} = \frac{3 \sqrt{3}}{4} π ({cm}^{2})$
B. $S_{x q} = \frac{2 \sqrt{3}}{3} π ({cm}^{2})$
C. $S_{x q} = \frac{\sqrt{3}}{2} π ({cm}^{2})$
D. $S_{x q} = 2 π ({cm}^{2})$
Câu 552 : Cho số phức $z = a + b i (a, b \in ℝ)$ thỏa điều kiện $(2 - 3 i) z - 7 i . z = 22 - 20 i$ . Tính a+b

A. 3
B. -4
C. -6
D. 2
Câu 553 : Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d_{1} : \frac{x - 3}{2} = \frac{y - 1}{- 1} = \frac{z - 2}{1}$ và $d_{2} : \frac{x - 5}{- 2} = \frac{y}{1} = \frac{z - 3}{- 1}$ . Xét vị trí tương đối của $d_{1}$ và $d_{2}$

A. $d_{1}$ và $d_{2}$ trùng nhau
B. $d_{1}$ và $d_{2}$ song song
C. $d_{1}$ và $d_{2}$ cắt nhau
D. $d_{2}$ và $d_{2}$ chéo nhau.

Câu 554 : Một kỹ sư được nhận lương khởi điểm là 8.000.000 đồng/tháng. Cứ sau hai năm lương mỗi tháng của kỹ sư đó được tăng thêm 10% so với mức lương hiện tại. Tính tổng số tiền T (đồng) kỹ sư đó nhận được sau 6 năm làm việc.

A. 633.600.000
B. 635.520.000
C. 696.960.000
D. 766.656.000
Câu 555 : Cho $f (x) = \sqrt{1 + 3 x} - \sqrt[3]{1 + 2 x}, g (x) = \sin x$ . Tính giá trị của $\frac{f' (0)}{g' (0)}$ .

A. $\frac{5}{6}$
B. $- \frac{5}{6}$
C. 0
D. 1
Câu 556 : Tìm tất cả các giá trị của tham số thực m sao cho hàm số $f (x) = \{\begin{cases} 2 \sqrt{x} - m k h i x \geq 0 \\ m x + 2 k h i x < 0 \end{cases}$ liên tục trên $ℝ$ .

A. m = 2
B. m = $\pm 2$
C. m = -2
D. m = 0
Câu 557 : Số tiếp tuyến của đồ thị hàm số $y = \frac{x^{3}}{x - 2} - 27$ song song với trục hoành là

A. 0
B. 1
C. 2
D. 3

Câu 558 : Trong mặt phẳng với hệ tọa độ Oxyz, cho $∆ A B C$ có A(2;4), B(5;1), C(-1;-2). Phép tịnh tiến $T_{\vec{B C}}$ biến $∆ A B C$ thành $∆ A' B' C'$ Tìm tọa độ trọng tâm của $∆ A' B' C'$

A. (-4;2)
B. (4;2)
C. (4;-2)
D. (-4;-2)
Câu 559 : Cho $\int_{1}^{3} f (x) d x = - 5, \int_{1}^{3} [f (x) - 2 g (x)] d x = 9$ . Tính $I = \int_{1}^{3} g (x) d x$ .

A. I = 14
B. I = -14
C. I = 7
D. I = -7
Câu 560 : Biết $\int_{\frac{π}{4}}^{\frac{π}{2}} \frac{x}{\sin^{2} x} d x = m π + nln 2 (m, n \in ℝ)$ , hãy tính giá trị của biểu thức P = 2m + n.

A. P = 1
B. P = 0,75
C. P = 0,25
D. P = 0
Câu 561 : Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): mx + 2y - z + 1 = 0 (m là tam số). Mặt phẳng (P) cắt mặt cầu (S): ${(x - 2)}^{2} + {(y - 1)}^{2} + z^{2} = 9$ theo một đường tròn có bán kính bằng 2. Tìm tất cả các giá trị thực của tham số m.

A. $m = \pm 1$
B. $m = \pm 2 + \sqrt{5}$
C. $m = 6 \pm 2 \sqrt{5}$
D. $m = \pm 4$

Câu 562 : Đồ thị hàm số $y = - x^{3} + 3 m x + 1$ có 2 điểm cực trị A,B $(x_{A} < x_{B})$ sao cho tứ giác ABOE là hình bình hạnh với O là gốc tọa độ và điểm E(-4;-32). Tìm tất cả các giá trị thực của tham số m.

A. m = 1
B. m = 4
C. m = 2
D. $m \in \emptyset$
Câu 563 : Tìm nguyên hàm của hàm số $f (x) = \sqrt{x} \ln x .$

A. $\int f (x) d x = \frac{1}{9} x^{\frac{3}{2}} (3 \ln x - 2) + C$
B. $\int f (x) d x = \frac{2}{3} x^{\frac{3}{2}} (3 \ln x - 2) + C$
C. $\int f (x) d x = \frac{2}{9} x^{\frac{3}{2}} (3 \ln x - 1) + C$
D. $\int f (x) d x = \frac{2}{9} x^{\frac{3}{2}} (3 \ln x - 2) + C$
Câu 564 : Có bao nhiêu số phức z thỏa mãn $|z| = |z + z| = 1$ ?

A. 0
B. 1
C. 4
D. 3
Câu 565 : Tập hợp các điểm biểu diễn số phức z thỏa mãn $2 |z - 1| = |z + z + 2|$ trên mặt phẳng tọa độ là một

A. đường thẳng
B. đường tròn
C. parabol
D. hypebol

Câu 566 : Người thợ gia công của một cơ sở chất lượng cao X cắt một miếng tôn hình tròn với bán kính 60cm thành ba miền hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miếng tôn đó để được ba cái phễu hình nón. Hỏi thể tích V của mỗi cái phễu đó bằng bao nhiêu?

A. $V = \frac{16000 \sqrt{2}}{3} l í t$
B. $V = \frac{16 \sqrt{2}}{3} l í t$
C. $V = \frac{16000 \sqrt{2} π}{3} l í t$
D. $V = \frac{160 \sqrt{2 π}}{3} l í t$
Câu 567 : Cho hàm số $f (x) = x^{3} - 6 x^{2} + 9 x + 1$ có đồ thị (C). Có bao nhiêu tiếp tuyến của đồ thị (C) tại điểm thuộc đồ thị (C) có tung độ là nghiệm phương trình $2 f' (x) - x . f'' (x) - 6 = 0$ ?

A. 1
B. 4
C. 2
D. 3
Câu 568 : Ông An muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng 288 $m^{3}$ . Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500.000 đồng/ $m^{2}$ . Nếu ông An biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi ông An trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu?

A. 108 triệu đồng
B. 54 triệu đồng
C. 168 triệu đồng
D. 90 triệu đồng
Câu 569 : Trong không gian với hệ tọa độ Oxyz , cho đường thẳng $d : \frac{x - 1}{1} = \frac{y - 2}{1} = \frac{z - 1}{2}$ , A(2;1;4). Gọi điểm H(a;b;c) là điểm thuộc d sao cho AH có độ dài nhỏ nhất. Tính giá trị T = $a^{2} + b^{2} + c^{2}$ .

A. T = 8
B. T = 62
C. T = 13
D. T = $\sqrt{5}$

Câu 570 : Cho hàm số $f (x) = 5^{x} . 8^{2 x^{3}}$ . Khẳng định nào sau đây là sai?

A. $f (x) \leq 1 \Leftrightarrow x \log_{2} 5 + 2 x^{3} \leq 0 .$
B. $f (x) \leq 1 \Leftrightarrow x + 6 x^{3} \log_{5} 2 \leq 0 .$
C. $f (x) \leq 1 \Leftrightarrow x \log_{2} 5 + 6 x^{3} \leq 0 .$
D. $f (x) \leq 1 \Leftrightarrow x \log_{2} \sqrt{5} + 3 x^{3} \leq 0 .$
Câu 571 : Có bao nhiêu giá trị nguyên của tham số m để hàm số $f (x) = 2 x^{3} - 6 x^{2} - m + 1$ có các giá trị cực trị trái dấu?

A. 2.
B. 9.
C. 3.
D. 7.
Câu 572 : Cho hàm số f(x) liên tục trên $ℝ$ và $\int_{0}^{1} f (x) d x = 2$ ; $\int_{0}^{3} f (x) d x = 6$ . Tính $I = \int_{- 1}^{1} f (|2 x - 1|) d x$ ?

A. $I = \frac{2}{3}$
B. $I = 4$
C. $I = \frac{3}{2}$
D. $I = 6$
Câu 573 : Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng $a \sqrt{3}$ . Gọi O là tâm của đáy ABC, $d_{1}$ là khoảng cách từ A đến mặt phẳng (SBC), $d_{2}$ là khoảng cách từ O đến mặt phẳng (SBC). Tính $d = d_{1} + d_{2}$ ?

A. $d = \frac{2 a \sqrt{22}}{11}$ .
B. $d = \frac{2 a \sqrt{22}}{33}$
C. $d = \frac{8 a \sqrt{22}}{33}$
D. $d = \frac{8 a \sqrt{22}}{11}$

Câu 574 : Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \frac{\sqrt{x^{2} - 1}}{x - 2}$ trên tập hợp $D = (- \infty; - 1) \cup [1; \frac{3}{2}]$ . Tính giá trị P = M.n?

A. $P = \frac{1}{9}$
B. $P = \frac{3}{2}$
C. $P = 0$
D. $P = - \frac{3}{2}$
Câu 575 : Đồ thị hàm số $y = a x^{4} + b x^{2} + c$ đạt cực đại tại A(0;-2) và cực tiểu tại $B (\frac{1}{2}; - \frac{17}{8})$ . Tính a + b + c

A. a + b + c = 2
B. a + b + c = 0
C. a + b + c = -1
D. a + b + c = -3
Câu 576 : Một cái th ng đựng nước được tạo thành từ việc cắt mặt xung quanh của một hình nón bởi một mặt phẳng vuông góc với trục của hình nón. Miệng thùng là đường tròn có bán kính bằng hai lần bán kính mặt đáy của th ng. Bên trong thùng có một cái phễu dạng hình nón có đáy là đáy của th ng, có đ nh là tâm của miệng thùng và có chiều cao bằng 20cm (xem hình minh họa). Biết rằng đổ 4.000 $c m^{3}$ nước vào th ng thì đầy th ng (nước không chảy được vào bên trong phễu), tính bán kính đáy r của phễu (giá trị gần đúng của r làm tròn đến hàng phần trăm).

A. r = 9,77 cm
B. r = 7,98 cm
C. r = 5,64 cm
D. r = 5,22 cm
Câu 577 : Cho tam giác SAB vuông tại A, ABS = 60 $°$ đường phân giác trong của ABS cắt SA tại điểm I. Vẽ nửa đường tròn tâm I bán kính IA (như hình vẽ). Cho $∆ S A B$ và nửa đường tròn trên quay quanh cạnh SA tạo nên các khối tròn xoay tương ứng có thể tích $V_{1}, V_{2}$ . Khẳng định nào dưới đây đúng?

A. $4 V_{1} = 9 V_{2}$
B. $9 V_{1} = 4 V_{2}$
C. $V_{1} = 3 V_{2}$
D. $2 V_{1} = 3 V_{2}$

Câu 578 : Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).

A. $3 x + 2 y + z + 14 = 0$
B. $2 x + y + 3 z + 9 = 0$
C. $3 x + 2 y + z - 14 = 0$
D. $2 x + y + z - 9 = 0$
Câu 579 : Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số $y = x^{4} - 2 m x^{2} + m - 1$ có ba điểm cực trị tạo thành một tam giác có bán kính đường tròn ngoại tiếp chúng bằng 1?

A. 1
B. 2
C. 3
D. 4
Câu 580 : Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} + a x + b y + c z + d = 0$ có bán kính $R = \sqrt{19}$ , đường thẳng $d : \{\begin{cases} x = 5 + t \\ y = - 2 - 4 t \\ z = - 1 - 4 t \end{cases}$ và mặt phẳng $(P) : 3 x - y - 3 z - 1 = 0$ . Trong các số {a,b,c,d} theo thứ tự dưới đây, số nào thỏa mãn a + b + c + d = 43, đồng thời tâm I của (S) thuộc đường thẳng d và (S) tiếp xúc với (P)?

A. {-6;-12;-14;75}
B. {6;10;20;7}
C. {-10;4;2;47}
D. {3;5;6;29}
Câu 581 : Cho phương trình $(m + 1) \log_{2}^{2} x + 2 \log_{2} x + (m - 2) = 0$ . Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực $x_{1}, x_{2}$ thỏa $0 < x_{1} < 1 < x_{2}$ .

A. $(2; + \infty)$
B. $(- 1; 2)$
C. $(- \infty; - 1)$
D. $(- \infty; - 1) \cup (2; + \infty)$

Câu 582 : Cho số phức z thỏa mãn $|z - 2 - 3 i| = 1$ . Gọi $M = m a x |\bar{z} + 1 + i|$ , $m = m i n |\bar{z} + 1 + i|$ . Tính giá trị của biểu thức $(M^{2} + m^{2})$

A. $M^{2} + m^{2} = 28$
B. $M^{2} + m^{2} = 26$
C. $M^{2} + m^{2} = 24$
D. $M^{2} + m^{2} = 20$
Câu 583 : Trong không gian với hệ tọa độ Oxyz, cho điểm A(9;-3;5), B(a,b,c). Gọi M, N, P lần lượt là giao điểm của đường thẳng AB với các mặt phẳng tọa độ (Oxy);(Oxz);(Oyz). Biết M,N,P nằm trên đoạn AB sao cho AN = MN = NP = PB. Giá trị của tổng a + b + c là

A. -21
B. 15
C. 21
D. -15
Câu 584 : Cho số phức z thỏa mãn $|\frac{z - 1}{2 - i} + i| = \sqrt{5}$ . Biết rằng tập hợp biểu diễn số phức w = (1 - i)z + 2i có dạng ${(x + 2)}^{2} + y^{2} = k$ . Tìm k.

A. k = 92
B. k = 100
C. k = 50
D. k = 96
Câu 585 : Đặt $f (n) = {(n^{2} + n + 1)}^{2} + 1$ . Xét dãy số $(u_{n})$ sao cho $u_{n} = \frac{f (1) f (3) f (5) . . . f (2 n - 1)}{f (2) f (4) f (6) . . . f (2 n)}$ . Tính $l i m (n \sqrt{n_{n}})$ .

A. $l i m (n \sqrt{n_{n}}) = \sqrt{2}$
B. $l i m (n \sqrt{n_{n}}) = \frac{1}{\sqrt{3}}$
C. $l i m (n \sqrt{n_{n}}) = \sqrt{3}$
D. $l i m (n \sqrt{n_{n}}) = \frac{1}{\sqrt{2}}$

Câu 586 : Tìm số phức liên hợp của số phức z thỏa mãn $(1 - i) z = 1 + 3 i$ .

A. $\bar{z} = - 1 + 2 i$
B. $\bar{z} = 1 - 2 i$
C. $\bar{z} = - 1 - 2 i$
D. $\bar{z} = 1 + 2 i$
Câu 587 : Trong không gian với hệ trục Oxyz, cho $\vec{a} = (2; - 1; 0)$ , biết $\vec{b}$ cùng chiều với $\vec{a}$ và có $|\vec{a} . \vec{b}| = 10$ . Chọn phương án đúng?

A. $\vec{b} = (- 6; 3; 0)$
B. $\vec{b} = (- 4; 2; 0)$
C. $\vec{b} = (6; - 3; 0)$
D. $\vec{b} = (4; - 2; 0)$
Câu 588 : Cho hàm số y = sin 2x. Khẳng định nào dưới đây đúng?

A. $y^{2} + {(y')}^{2} = 1$
B. $y = y' \tan 2 x$
C. $4 y + y'' = 0$
D. $4 y - y' = 0$
Câu 589 : Biết $\log_{7} 2 = m$ , khi đó giá trị của $\log_{49} 28$ được tính theo m là:

A. $\frac{1 + 2 m}{2}$
B. $\frac{m + 2}{4}$
C. $\frac{1 + m}{2}$
D. $\frac{1 + 4 m}{2}$

Câu 590 : $\int f (x) d x = \frac{1}{x} + \ln |5 x| + C$ với $x \in (0; + \infty)$ thì hàm số f(x) là

A. $f (x) = \sqrt{x} + \frac{1}{5 x}$
B. $f (x) = - \frac{1}{x^{2}} + \frac{1}{5 x}$
C. $f (x) = - \frac{1}{x^{2}} + \frac{1}{x}$
D. $f (x) = - \frac{1}{x^{2}} + \ln (5 x)$
Câu 591 : Tổng của n số hạng đầu tiên của một dãy số $(a_{n}), n \geq 1$ là $S_{n} = 2 n^{2} + 3 n$ . Khi đó

A. $(a_{n})$ là một cấp số cộng với công sai bằng 4
B. $(a_{n})$ là một cấp số nhân với công bội bằng 4
C. $(a_{n})$ là một cấp số cộng với công sai bằng 1
D. $(a_{n})$ là một cấp số nhân với công bội bằng 1
Câu 592 : Cho tứ diện ABCD. Hỏi có bao nhiêu vectơ khác vectơ $\vec{0}$ mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD

A. 12
B. 4
C. 10
D. 8
Câu 593 : Cho F(x) là một nguyên hàm của hàm số $f (x) = \frac{2}{\cos^{2} x}$ và $F (\frac{π}{4}) = - 3$ . Khẳng định nào dưới đây đúng?

A. $F (x) = - 2 c o t x - 5$
B. $F (x) = 2 \tan x + 3$
C. $F (x) = \tan x - 4$
D. $F (x) = 2 \tan x - 5$

Câu 594 : Cho $f (x) = \frac{1}{2} . 5^{2 x + 1}; g (x) = 5^{x} + 4 x . \ln 5$ . Tập nghiệm của bất phương trình $f' (x) > g' (x)$ là

A. x < 0
B. x > 1
C. 0 < x < 1
D. x > 0
Câu 595 : Tập nghiệm của bất phương trình ${(\sqrt{5} - 2)}^{\frac{2 x}{x - 1}} \leq {(\sqrt{5} + 2)}^{x}$ là

A. $(- \infty; - 1] \cup [0; 1)$
B. [-1;0]
C. $(- \infty; - 1) \cup [0; + \infty)$
D. $[- 1; 0] \cup (1; + \infty)$
Câu 596 : Cho hàm số y = f(x) xác định trên $ℝ \ \{1\}$ , liên tục trên các khoảng xác định của nó và có bảng biến thiên như hình vẽ:

A. Đồ thị hàm số có 3 tiệm cận.
B. Phương trình f(x) = m có 3 nghiệm thực phân biệt thì $m \in (1; 2)$ .
C. Giá trị lớn nhất của hàm số là 2.
D. Hàm số đồng biến trên $(- \infty; 1)$ .
Câu 597 : Trong không gian với hệ trục Oxyz cho điểm A(1;2;1) và đường thẳng có phương trình $(d) : \frac{x + 1}{1} = \frac{y - 2}{- 1} = \frac{z}{1}$ . Viết phương trình mặt phẳng chứa A và vuông góc với d.

A. x - y + z - 1 = 0
B. x - y + z - 1 = 0
C. x - y + z = 0
D. x - y + z - 2 = 0

Câu 598 : Biết tập nghiệm S của bất phương trình $\log_{\frac{π}{6}} [\log_{3} (x - 2)] > 0$ là khoảng (a;b). Tính b - a.

A. 2
B. 4
C. 3
D. 5
Câu 599 : Biết $I = \int_{0}^{4} x \ln (2 x + 1) d x = \frac{a}{b} \ln 3 - c$ , trong đó a, b, c là các số nguyên dương và $\frac{a}{b}$ là phân số tối giản. Tính S = a + b + c.

A. S = 60
B. S = 70
C. S = 72
D. S = 68
Câu 600 : Cho hàm số $y = \log_{\frac{1}{3}} (x^{3} - 2 x)$ . Tập nghiệm của bất phương trình y' > 0 là:

A. $(- \infty; 1)$
B. $(- \infty; 0)$
C. $(1; + \infty)$
D. $(2; + \infty)$
Câu 601 : Tập xác định của hàm số $y = \log_{2} (3^{x} - 2)$ là

A. $(0; + \infty)$
B. $[0; + \infty)$
C. $(\frac{2}{3}; + \infty)$
D. $(\log_{3} 2; + \infty)$

Câu 602 : Điểm M trong hình vẽ là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo của số phức.

A. Phần thực là -3 và phần ảo là 2.
B. Phần thực là 2 và phần ảo là -3.
C. Phần thực là -3 và phần ảo là 2i.
D. Phần thực là 2 và phần ảo là -3i.
Câu 603 : Cho hàm số $y = \frac{a x + 1}{b x - 2}$ . Tìm a, b để đồ thị hàm số có x = 1 là tiệm cận đứng và $y = \frac{1}{2}$ là tiệm cận ngang.

A. a = -1; b = -2
B. a = 1; b = 2
C. a = -1; b = 2
D. a = 4; b = 4
Câu 604 : Một hình trụ có diện tích xung quanh bằng $4 π$ thiết diện qua trục là hình vuông. Một mặt phẳng $(α)$ song song với trục, cắt hình trụ theo thiết diện là tứ giác ABB’A’, biết một cạnh của thiết diện là một dây cung của đường tròn đáy của hình trụ và căng một cung $120 °$ . Tính diện tích thiết diện ABB’A’?

A. $3 \sqrt{2}$
B. $\sqrt{3}$
C. $2 \sqrt{3}$
D. $2 \sqrt{2}$
Câu 605 : Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B, biết rằng các cạnh SA = AC = 2. Tính theo a thể tích của khối chóp S.ABC.

A. $\frac{2 \sqrt{2}}{3} a^{3}$
B. $\frac{1}{3} a^{3}$
C. $\frac{2}{3} a^{3}$
D. $\frac{4}{3} a^{3}$

Câu 606 : Có bao nhiêu số phức z thỏa mãn: $|z - i| = \sqrt{2}$ và $z^{2}$ là số thuần ảo:

A. 3
B. 1
C. 4
D. 2
Câu 607 : Cho tích phân $I = \int_{0}^{\frac{π}{4}} (x - 1) \sin 2 x d x$ . Tìm đẳng thức đúng

A. $I = - (x - 1) {\cos 2 x}_{0}^{\frac{π}{4}} + \int_{0}^{\frac{π}{4}} \cos 2 x d x$
B. $I = - (x - 1) c o s 2 x - \int_{0}^{\frac{π}{4}} \cos 2 x d x$
C. $I = - \frac{1}{2} (x - 1) {\cos 2 x}_{0}^{\frac{π}{4}} + \frac{1}{2} \int_{0}^{\frac{π}{4}} \cos 2 x d x$
D. $I = - \frac{1}{2} (x - 1) {\cos 2 x}_{0}^{\frac{π}{4}} - \int_{0}^{\frac{π}{4}} \cos 2 x d x$
Câu 608 : Gọi $z_{1}, z_{2}, z_{3}, z_{4}$ là bốn nghiệm phức của phương trình $z^{2} - 2 z^{2} - 8 = 0$ . Trên mặt phẳng tọa độ, gọi A, B, C, D lần lượt là bốn điểm biểu diễn bốn nghiệm của $z_{1}, z_{2}, z_{3}, z_{4}$ . Tính giá trị của P = OA + OB + OC + OD trong đó O là gốc tọa độ.

A. P = 4
B. P = $2 + \sqrt{2}$
C. P = $2 \sqrt{2}$
D. P = $4 + 2 \sqrt{2}$
Câu 609 : Có bao nhiêu số $a \in (0; 20 π)$ sao cho $\int_{0}^{a} \sin^{5} x . \sin 2 x d x = \frac{2}{7}$ .

A. 20
B. 19
C. 9
D. 10

Câu 610 : Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu $(S) : {(x - 2)}^{2} + {(y + 1)}^{2} + {(z - 3)}^{2} = 9$ . Mệnh đề nào sau đây là đúng?

A. Mặt cầu (S) tiếp xúc với (Oxy).
B. Mặt cầu (S) không tiếp xúc với cả ba mặt (Oxy), (Oxz), (Oyz).
C. Mặt cầu (S) tiếp xúc với (Oyz).
D. Mặt cầu (S) tiếp xúc với (Oxz).
Câu 611 : Cho hàm số $y = |2 x^{2} - 3 x - 1|$ . Giá trị lớn nhất của hàm số trên $[\frac{1}{2}; 2]$ là:

A. $\frac{17}{8}$
B. $\frac{9}{4}$
C. 2
D. 3
Câu 612 : Biết hàm số $F (x) = a x^{3} + (a + b) x^{2} + (2 a - b + c) x + 1$ là một nguyên hàm của hàm số $f (x) = 3 x^{2} + 6 x + 2$ . Tổng a + b + c là:

A. 5
B. 4
C. 3
D. 2
Câu 613 : Cho hàm số $f (x) = \frac{4^{x}}{4^{x} + 2}$ . Tính giá trị biểu thức $A = f (\frac{1}{100}) + f (\frac{2}{100}) + . . . + f (\frac{100}{100})$ ?

A. 50
B. 49
C. $\frac{149}{3}$
D. $\frac{301}{6}$

Câu 614 : Cho A, B, C là những điểm biểu diễn các số phức thỏa mãn $z^{3} + i = 0$ . Tìm phát biểu sai?

A. Tam giác ABC đều
B. Tam giác ABC có trọng tâm là O(0;0)
C. Tam giác ABC có tâm đường tròn ngoại tiếp là O(0;0)
D. $S_{A B C} = \frac{3 \sqrt{3}}{2}$
Câu 615 : Cho (H) là hình phẳng giới hạn bởi $y = \sqrt{x}, y = x - 2$ và trục hoành (hình vẽ).

A. $\frac{10}{3}$
B. $\frac{16}{3}$
C. $\frac{7}{3}$
D. $\frac{8}{3}$
Câu 616 : Cho hình trụ có trục OO’, thiết diện qua trục là một hình vuông cạnh 2a. Mặt phẳng (P) song song với trục và cách trục một khoảng $\frac{a}{2}$ . Tính diện tích thiết diện của trục cắt bởi mặt phẳng

A. $a^{2} \sqrt{3}$
B. $a^{2}$
C. $2 a^{2} \sqrt{3}$
D. $π a^{2}$
Câu 617 : Trong không gian với hệ trục Oxyz cho điểm A(1;2;1) và mặt phẳng $(P) : x + 2 y - 2 z = 0$ . Gọi B là điểm đối xứng với A qua (P). Độ dài đoạn AB là:

A. 2
B. $\frac{4}{3}$
C. $\frac{2}{3}$
D. 4

Câu 618 : Có bao nhiêu số có bốn chữ số đôi một khác nhau và chia hết cho 5 được lập từ các chữ số 0, 1, 2, 3, 4, 5, 6?

A. 360
B. 220
C. 240
D. 180
Câu 619 : Số hạng không chứa x trong khai triển ${(2 x - \frac{3}{\sqrt[3]{x}})}^{2 n}$ với $x \neq 0$ , biết n là số nguyên dương thỏa mãn $C_{n}^{3} + 2 n = A_{n + 1}^{2}$ là

A. $- C_{16}^{12} . 2^{4} . 3^{12}$
B. $C_{16}^{0} . 2^{16}$
C. $C_{16}^{12} . 2^{4} . 3^{12}$
D. $C_{16}^{16} . 2^{0}$
Câu 620 : Cho hàm số y = f(x) có đạo hàm trên $ℝ$ và có đồ thị hàm số y = f '(x) như hình vẽ bên. Xét hàm số $g (x) = f (x^{3} - 2)$ Mệnh đề nào sau đây là sai?

A. Hàm số g(x) nghịch biến trên khoảng (-1;0)
B. Hàm số g(x) nghịch biến trên khoảng $(- \infty; - 2)$
C. Hàm số g(x) nghịch biến trên khoảng (0;2)
D. Hàm số g(x) đồng biến trên khoảng $(2; + \infty)$
Câu 621 : Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh SA=2a và SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của cạnh AB và $(α)$ là mặt phẳng qua M và vuông góc với AB. Diện tích thiết diện của mặt phẳng với hình chóp S.ABCD là

A. $S = a^{2}$
B. $S = \frac{3 a^{2}}{2}$
C. $S = \frac{a^{2}}{2}$
D. $S = 2 a^{2}$

Câu 622 : Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;-3;7), B(0;4;-3), C(4;2;5). Biết điểm M( $x_{0}; y_{0}; z_{0}$ ) nằm trên mặt phẳng (Oxy) sao cho $|\vec{M A} + \vec{M B} + \vec{M C}|$ có giá trị nhỏ nhất. Khi đó giá trị của tổng $P = x_{0} + y_{0} + z_{0}$ bằng

A. P = 0
B. P = 6
C. P = 3
D. P = -3
Câu 623 : Cho hàm số f(x) xác định trên $ℝ \ \{- 1; 1\}$ và thỏa mãn $f' (x) = \frac{1}{x^{2} - 1}$ . Biết f(-3) + f(3) = 0 và $f (- \frac{1}{2}) + f (\frac{1}{2}) = 2$ . Tính giá trị $T = f (- 2) + f (0) + f (4)$ .

A. $T = 1 + \ln \frac{9}{5}$
B. $T = 1 + \ln \frac{6}{5}$
C. $T = 1 + \frac{1}{2} \ln \frac{9}{5}$
D. $T = 1 + \frac{1}{2} \ln \frac{6}{5}$
Câu 624 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA = 2a. Gọi B’, D’ lần lượt là hình chiếu vuông góc của A trên các cạnh SB, SD. Mặt phẳng (AB’D’) cắt cạnh SC tại C’. Tính thể tích của khối chóp S.AB’C’D’.

A. $\frac{a^{3}}{3}$
B. $\frac{16 a^{3}}{45}$
C. $\frac{a^{3}}{2}$
D. $\frac{a^{3} \sqrt{2}}{2}$
Câu 625 : Một viên phấn bảng có dạng một khối trụ với bán kính đáy bằng 0,5cm, chiều dài 6cm. Người ta làm một hình hộp chữ nhật bằng carton đựng các viên phấn đó với kích thước 6cm x 5cm x 6cm. Hỏi cần ít nhất bao nhiêu hộp kích thước như trên để xếp 460 viên phấn?

A. 17
B. 15
C. 16
D. 18

Câu 626 : Cho số phức thỏa mãn $|z| \leq 1$ . Đặt $A = \frac{2 z - 1}{2 + i z}$ . Mệnh đề nào sau đây đúng?

A. $|A| \leq 1$
B. $|A| \geq 1$
C. $|A| < 1$
D. $|A| > 1$
Câu 627 : Một nguồn âm đẳng hướng đặt tại điểm O có công suất truyền âm không đổi. Mức cường độ âm tại điểm M cách O một khoảng R được tính bởi công thức $L_{M} = \log \frac{k}{R^{2}}$ (Ben) với k là hằng số. Biết điểm O thuộc đoạn thẳng AB và mức cường độ âm tại A và B lần lượt là $L_{A} = 3$ (Ben) và $L_{B} = 5$ (Ben). Tính mức cường độ âm tại trung điểm AB (làm tròn đến 2 chữ số sau dấu phẩy).

A. 3,59 (Ben).
B. 3,06 (Ben).
C. 3,69 (Ben).
D. 4 (Ben).
Câu 628 : Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f (x) = \sqrt{1 + \sin x} + \sqrt{1 + \cos x}$ . Tính giá trị của M - m.

A. $4 \sqrt{2}$
B. $3 + 2 \sqrt{2}$
C. $\sqrt{4 + 2 \sqrt{2}} - 1$
D. $4 + 2 \sqrt{2}$
Câu 629 : Trong không gian với hệ trục tọa độ Oxyz, cho A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c dương. Biết A, B, C di động trên các tia Ox, Oy, Oz sao cho a + b + c = 2. Biết rằng a, b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ M(2016;0;0) tới mặt phẳng (P).

A. 2017
B. $\frac{2014}{\sqrt{3}}$
C. $\frac{2016}{\sqrt{3}}$
D. $\frac{2015}{\sqrt{3}}$

Câu 630 : Cho số phức z thỏa mãn $|z - 3 - 4 i| = \sqrt{5}$ . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P = {|z + 2|}^{2} - {|z - i|}^{2}$ . Tính môđun của số phức w = M + mi ?

A. $|w| = \sqrt{2315}$
B. $|w| = \sqrt{1258}$
C. $|w| = 3 \sqrt{137}$
D. $|w| = 2 \sqrt{309}$
Câu 631 : Cho hàm số f(x)có đạo hàm liên tục trên [0;1] thỏa $\int_{0}^{1} [f (x)] d x = \int_{0}^{1} (x + 1) e^{x} f (x) d x = \frac{e^{2} - 1}{4}$ và f(1) = 0. Tính $\int_{0}^{1} f (x) d x$ .

A. $\frac{e - 1}{2}$
B. $\frac{e^{2}}{4}$
C. $e - 2$
D. $\frac{e}{2}$
Câu 632 : Một công ty mỹ phẩm chiết xuất $1 (m^{3})$ hoạt chất đặc biệt và họ sử dụng nó để sản suất ra một sản phẩm kem dưỡng da mới với thiết kế hộp là một khối cầu có đường kính $\sqrt{108} c m$ bên trong hộp là một khối trụ nằm trong nửa khối cầu để đựng kem dưỡng da (như hình vẽ). Để thu hút khác hàng công ty đã thiết kế khối trụ có thể tích lớn nhất để đựng kem dưỡng da. Hỏi với $1 (m^{3})$ hoạt chất đặc biệt trên, công ty đó sản xuất được tối đa bao nhiêu hộp sản phẩm, biết rằng trong kem dưỡng da chỉ chứa 0,3% hoạt chất đặc biệt trên ?

A. 1964875 hộp
B. 2254715 hộp
C. 2084645 hộp
D. 1754845 hộp
Câu 633 : Cho khối trụ (T)có bán kính đáy bằng R và diện tích toàn phần bằng $8 {πR}^{2}$ . Tính thể tích V của khối trụ (T).

A. $6 {πR}^{3}$
B. $3 {πR}^{3}$
C. $4 {πR}^{3}$
D. $8 {πR}^{3}$

Câu 634 : Tìm nghiệm của phương trình $\frac{3^{2 x - 6}}{27} = {(\frac{1}{3})}^{x}$ .

A. x = 4
B. x = 2
C. x = 5
D. x = 3
Câu 635 : Biết $\int f (x) d x = 2 x \ln (3 x - 1) + C$ với $x \in (\frac{1}{3}; + \infty)$ . Tìm khẳng định đúng trong các khẳng định sau

A. $\int f (3 x) d x = 2 x \ln (9 x - 1) + C$
B. $\int f (3 x) d x = 6 x \ln (3 x - 1) + C$
C. $\int f (3 x) d x = 6 x \ln (9 x - 1) + C$
D. $\int f (3 x) d x = 3 x \ln (9 x - 1) + C$
Câu 636 : Cho dãy số $(u_{n})$ biết $\{\begin{cases} u_{1} = 2 \\ u_{n + 1} = 2 u_{n} \forall n \in ℕ * \end{cases}$ . Tìm số hạng tổng quát của dãy số này ?

A. $u_{n} = 2^{n}$
B. $u_{n} = n^{n - 1}$
C. $u_{n} = 2$
D. $u_{n} = 2^{n + 1}$
Câu 637 : Cho hàm số $f (x) = \{\begin{cases} \frac{\sqrt{x^{2} + 1} - 1}{x} k h i x \neq 0 \\ 0 k h i x = 0 \end{cases}$ . Tính $f' (0)$ ?

A. $\frac{1}{2}$
B. Không tồn tại
C. 1
D. 0

Câu 638 : Hàm số $y = a x^{3} + b x^{2} + c x + d$ đồng biến trên $ℝ$ khi và chỉ khi

A. $[\begin{array}{l} a = b = 0, c > 0 \\ a > 0; b^{2} - 3 a c > 0 \end{array}$
B. $[\begin{array}{l} a = b = 0, c > 0 \\ a < 0; b^{2} - 3 a c \leq 0 \end{array}$
C. $[\begin{array}{l} a = b = 0, c > 0 \\ a > 0; b^{2} - 3 a c \leq 0 \end{array}$
D. $a > 0; b^{2} - 3 a c \leq 0$
Câu 639 : Tính $\lim_{x \to 3^{+}} \frac{x - 3}{\sqrt{x^{2} - 9}}$ ?

A. $- \infty$
B. 0
C. $\sqrt{6}$
D. $+ \infty$
Câu 640 : Tìm tập xác định của D của hàm số $y = {(x^{2} - 1)}^{- 2}$ .

A. $D = ℝ$
B. $D = (- \infty; - 1) \cup (1; + \infty)$
C. $D = (- 1; 1)$
D. $D = ℝ \ \{\pm 1\}$
Câu 641 : Cho phương trình $5^{x + 5} = 8^{x}$ . Biết phương trình có nghiệm $x = \log_{a} 5^{5}$ , trong đó $0 < a \neq 1$ . Tìm phần nguyên của a.

A. 0
B. 1
C. 2
D. 3

Câu 642 : Một hình trụ có bán kính đáy bằng r và khoảng cách giữa hai đáy bằng $r \sqrt{3}$ . Một hình nón có đỉnh là tâm mặt đáy này và đáy trùng với mặt đáy kia của hình trụ. Tính tỉ số diện tích xung quanh của hình trụ và hình nón.

A. $\sqrt{3}$
B. $\frac{1}{\sqrt{3}}$
C. $\frac{1}{3}$
D. 3
Câu 643 : Nếu gọi $(G_{1})$ là đồ thị hàm số $y = a^{x}$ và $(G_{2})$ là đồ thị hàm số $y = \log_{a} x$ với $0 < a \neq 1$ . Mệnh đề nào dưới đây đúng?

A. $(G_{1})$ và $(G_{2})$ đối xứng với nhau qua trục hoành
B. $(G_{1})$ và $(G_{2})$ đối xứng với nhau qua trục tung
C. $(G_{1})$ và $(G_{2})$ đối xứng với nhau qua đường thẳng y = x
D. $(G_{1})$ và $(G_{2})$ đối xứng với nhau qua đường thẳng y = -x
Câu 644 : Cho $\int_{1}^{3} f (x) d x = 2$ và $\int_{1}^{3} g (x) d x = 1$ . Tính $\int_{1}^{3} [1008 f (x) + 2 g (x)] d x$ .

A. x = 2017
B. x = 2016
C. x = 2019
D. x = 2018
Câu 645 : Cho hàm số y = f(x) có đạo hàm $f' (x) = {(x + 1)}^{2} (2 - x) (x + 3)$ . Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng (-3;2)
B. Hàm số nghịch biến trên các khoảng $(- 3; - 1) v à (2; + \infty)$
C. Hàm số đồng biến trên các khoảng $(- \infty; - 3) v à (2; + \infty)$
D. Hàm số đồng biến trên khoảng (-3;2)

Câu 646 : Cho hàm số y = f(x) có bảng biến thiên dưới đây.

A. $m \in (- 2; 2)$
B. $m \in (- 1; 3) \ \{0; 2\}$
C. $m \in (- 1; 3)$
D. $m \in [- 1; 3] \ \{0; 2\}$
Câu 647 : Biết $I = \int_{1}^{5} \frac{2 |x - 2| + 1}{x} d x = 4 + a \ln 2 + b \ln 5$ , với a, b là các số nguyên. Tính $S = a - b$

A. S = 9
B. S = 11
C. S = 5
D. S = -3
Câu 648 : Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;4;1), B(-1;1;3) và mặt phẳng (P):x - 3y + 2z - 5 = 0. Viết phương trình mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P).

A. $(Q) : 2 y + 3 z - 1 = 0$
B. $(Q) : 2 x + 3 z - 12 = 0$
C. $(Q) : 2 x + 3 z - 11 = 0$
D. $(Q) : 2 y + 3 z - 11 = 0$
Câu 649 : Cho $\int_{0}^{\frac{π}{2}} f (x) d x = 5$ . Tính $I = \int_{0}^{\frac{π}{2}} [f (x) + 2 \sin (x)] d x$ .

A. I = $5 + π$
B. I = $5 + \frac{π}{2}$
C. I = 3
D. I = 7

Câu 650 : Cho hình chữ nhật ABCD có AB = 2a, BC = 3a. Gọi M, N lần lượt là các điểm trên cạnh AD, BC sao cho MA = 2MD, NB = 2NC. Khi quay quanh AB, các đường gấp khúc AMNB, ADCB sinh ra các hình trụ có diện tích toàn phần $S_{1}, S_{2}$ Tính tỉ số $\frac{S_{1}}{S_{2}}$ là:

A. $\frac{S_{1}}{S_{2}} = \frac{12}{21}$
B. $\frac{S_{1}}{S_{2}} = \frac{2}{3}$
C. $\frac{S_{1}}{S_{2}} = \frac{4}{9}$
D. $\frac{S_{1}}{S_{2}} = \frac{8}{15}$
Câu 651 : Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P):x + 2y + 2z + 1 = 0 và đường thẳng $d : \frac{x - 1}{2} = \frac{y - 1}{2} = \frac{z}{1}$ . Gọi I là giao điểm của d và (P), điểm M là điểm trên đường thẳng d sao cho IM = 9, tính khoảng cách từ điểm M đến mặt phẳng (P).

A. $d (M; (P)) = 8$
B. $d (M; (P)) = 2 \sqrt{2}$
C. $d (M; (P)) = 4$
D. $d (M; (P)) = 3 \sqrt{2}$
Câu 652 : Gọi $z_{1}, z_{2}$ là hai nghiệm của phương trình $z^{2} - 2 z + 2 = 0, (z \in C)$ . Tính giá trị của biểu thức $P = 2 |z_{1} + z_{2}| + |z_{1} - z_{2}|$ .

A. P = 6
B. P = 3
C. P = $2 \sqrt{2} + 2$
D. P = $\sqrt{2} + 4$
Câu 653 : Gọi M, m thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \frac{x^{2} + 3}{x - 1}$ trên đoạn [-2;0]. Tính P = M + m.

A. P = 1
B. P = 3
C. P = -5
D. P = 5

Câu 654 : Tìm tất cả các số thực m dương thỏa mãn $\int_{0}^{m} \frac{x^{2} d x}{x + 1} = \ln 2 - \frac{1}{2}$

A. m = 3
B. m = 2
C. m = 1
D. m > 3
Câu 655 : Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;1;0) và đường thẳng $∆ : \frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z}{- 1}$ . Viết phương trình của đường thẳng đi d đi qua điểm M, căt và vuông góc với $∆$ .

A. $d : \frac{x - 2}{1} = \frac{y - 1}{4} = \frac{z}{1}$
B. $d : \frac{x - 2}{1} = \frac{y - 1}{- 4} = \frac{z}{1}$
C. $d : \frac{x - 2}{2} = \frac{y - 1}{- 4} = \frac{z}{1}$
D. $d : \frac{x - 2}{1} = \frac{y - 1}{- 4} = \frac{z}{- 2}$
Câu 656 : Giả sử F(x) là một nguyên hàm của hàm số $f (x) = \frac{e^{x}}{x}$ trên khoang $(0; + \infty)$ và $I = \int_{1}^{3} \frac{e^{3 x}}{x} d x$ . Khẳng định nào sau đây là khẳng định đúng?

A. $I = F (3) - F (1)$
B. $I = F (6) - F (3)$
C. $I = F (9) - F (3)$
D. $I = F (4) - F (2)$
Câu 657 : Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC),AC =AD = 4, AB =3, BC = 5. Tính khoảng cách d từ điểm A đến mặt phẳng (BCD).

A. $d = \frac{12}{\sqrt{34}}$
B. $d = \frac{60}{\sqrt{769}}$
C. $d = \frac{\sqrt{769}}{60}$
D. $d = \frac{\sqrt{34}}{12}$

Câu 658 : Cho hình phẳng (H) giới hạn bởi các đường y = lnx, y = 0, x = k (k > 1). Tìm k để diện tích hình phẳng (H) bằng 1

A. k = 2
B. $k = e^{3}$
C. $k = e^{3}$
D. k = 3
Câu 659 : Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = sinx + cosx + mx đồng biến trên $ℝ$

A. $- \sqrt{2} \leq m \leq \sqrt{2}$
B. $m \leq - \sqrt{2}$
C. $- \sqrt{2} < m < \sqrt{2}$
D. $m \geq \sqrt{2}$
Câu 660 : Cho tứ diện đều ABCD. Biết khoảng cách từ A đến mặt phẳng (BCD) bằng 6. Tính thể tích V tứ diện đều ABCD.

A. $V = 5 \sqrt{3}$
B. $V = 27 \sqrt{3}$
C. $V = \frac{27 \sqrt{3}}{2}$
D. $V = \frac{9 \sqrt{3}}{2}$
Câu 661 : Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AC = $a \sqrt{2}$ , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng 60 $°$ .Tính theo a thể tích V của khối chóp S. ABC.

A. $V = \frac{\sqrt{3} a^{3}}{2}$
B. $V = \frac{\sqrt{3} a^{3}}{4}$
C. $V = \frac{\sqrt{3} a^{3}}{6}$
D. $V = \frac{\sqrt{3} a^{3}}{12}$

Câu 662 : Cho hình chóp S.ABCD. Gọi A', B' , C', D' theo thứ tự là trung điểm của SA, SB, SC, SD. Tính tỉ số thể tích của hai khối chóp S.A'B'C'D' và S.ABCD.

A. $\frac{1}{16}$
B. $\frac{1}{4}$
C. $\frac{1}{8}$
D. $\frac{1}{2}$
Câu 663 : Phương trình nào dưới đây tương đương với phương trình $\cos 2 x + \sin 3 x = 1 + 2 \sin x . \cos 2 x$ ?

A. $s i n x = \frac{1}{2}$
B. $s i n x = 0$
C. $2 s i n^{2} x = \sin x$
D. $2 s i n^{2} x + \sin x = 0$
Câu 664 : Xác định các giá trị m để đường thẳng y = 3x + m +2 cắt đồ thị hàm số $y = - 3 x^{3} + 4 x + 2$ tại đúng một điểm.

A. $0 < m > \frac{2}{9}$
B. $|m| > \frac{2}{9}$
C. $m \neq \frac{2}{9}$
D. Không có m
Câu 665 : Trong tất cả các cặp số (x,y) thỏa mãn $\log_{x^{2} + y^{2} + 3} (2 x + 2 y + 5) \geq 1$ , giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho $x^{2} + y^{2} + 4 x + 6 y + 13 - m = 0$ thuộc tập nào sau đây?

A. [8;10]
B. [5;7]
C. [1;4]
D. [-3;0]

Câu 666 : Cho hình hộp chữ nhật ABCD.A' B' C' D' có tổng diện tích của tất cả các mặt là 36, độ dài đường chéo AC' bằng 6. Hỏi thể tích của khối hộp lớn nhất là bao nhiêu?

A. 8
B. $8 \sqrt{2}$
C. $16 \sqrt{2}$
D. $24 \sqrt{3}$
Câu 667 : Cho hàm số $y = \frac{2 x - 3}{x - 2} (C)$ . Gọi d là tiếp tuyến bất kì của (C), d cắt nhau đường tiệm cận của đồ thị (C) lần lượt tại A, B. Khi đó khoảng cách giữa A và B ngắn nhất bằng

A. $3 \sqrt{2}$
B. 4
C. $2 \sqrt{2}$
D. $3 \sqrt{3}$
Câu 668 : Trong không gian với hệ tọa độ Oxyz. Viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại ba điểm A, B, C khác với gốc tọa độ O sao cho biểu thức $\frac{1}{O A^{2}} + \frac{1}{O B^{2}} + \frac{1}{O C^{2}}$ có giá trị nhỏ nhất.

A. $(P) : x + 2 y + 3 z - 14 = 0$
B. $(P) : x + 2 y + 3 z - 11 = 0$
C. $(P) : x + 2 y + z - 8 = 0$
D. $(P) : x + y + 3 z - 14 = 0$
Câu 669 : Cho a, b là hai số thực dương khác 1 và thỏa mãn $\log_{2}^{a} b - 8 \log_{b} (a \sqrt[3]{b}) = - \frac{8}{3}$ . Tính giá trị biểu thức $P = \log_{a} (a \sqrt[3]{a b}) + 2017$ .

A. P = 2019
B. P = 2020
C. P = 2017
D. P = 2016

Câu 670 : Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình $x . 2^{x} = x (x - m + 1) + m (2^{x} - 1)$ có hai phần tử.Tìm số phần tử của A.

A. 1
B. Vô số
C. 3
D. 2
Câu 671 : Cho các số thực dương x, y thỏa mãn log(x + 2y) = log x + log y .Tìm giá trị nhỏ nhất của biểu thức $P = \sqrt[4]{e^{\frac{x^{2}}{1 + 2 y}}} . e^{\frac{y^{2}}{1 + 2 x}}$

A. $m i n P = e^{\frac{5}{8}}$
B. $m i n P = e$
C. $m i n P = e^{\frac{8}{5}}$
D. $m i n P = e^{\frac{1}{2}}$
Câu 672 : Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x + 2y + 2z + 18= 0, M là điểm di chuyển trên mặt phẳng (P), N là điểm nằm trên tia OM sao cho $\vec{O M} . \vec{O N} = 24$ . Tìm giá trị nhỏ nhất của khoảng cách từ điểm N đến mặt phẳng (P).

A. $m i n d (N; (P)) = 6$
B. $m i n d (N; (P)) = 4$
C. $m i n d (N; (P)) = 2$
D. $m i n d (N; (P)) = 0$
Câu 673 : Cho hàm số : $y = x^{3} = 2018 x$ có đồ thị là (C) M là điểm trên (C) có hoành $x_{1} = 1$ . Tiếp tuyến của (C) tại M cắt (C) tại điểm $M_{2}$ khác $M_{1}$ , tiếp tuyến của (C) tại $M_{2}$ cắt (C) tại điểm $M_{3}$ khác $M_{2}$ , tiếp tuyến của (C) tại điểm $M_{n - 1}$ cắt (C) tại điểm $M_{n}$ khác $M_{n - 1} (n = 4, 5, . . .)$ , gọi $(x_{n}; y_{n})$ là tọa độ điểm $M_{n}$ . Tìm n để : $2018 x_{n} + y_{n} + 2^{2019} = 0$

A. n = 647
B. n = 675
C. n = 674
D. n = 627

Câu 674 : Cho a là số thực dương. Biết rằng F(x) là một nguyên hàm của hàm số $f (x) = e^{x} (\ln (a x) + \frac{1}{x})$ thỏa mãn $F (\frac{1}{a}) = 0$ và $F (2018) = e^{2018}$ . Mệnh đề nào sau đây đúng?

A. $a \in (\frac{1}{2018}; 1)$
B. $a \in (0; \frac{1}{2018}]$
C. $a \in [1; 2018)$
D. $a \in [2018; + \infty)$
Câu 675 : Cho hàm số y = f(x) có đồ thị y = f ' (x) như hình bên. Gọi M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f(x) trên $[0; \frac{9}{2}]$ . Hỏi mệnh đề nào sau đây đúng?

A. $M = f (\frac{9}{2}), m = f (4)$
B. $M = f (0), m = f (4)$
C. $M = f (2), m = f (1)$
D. $M = f (\frac{9}{2}), m = f (1)$
Câu 676 : Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt (A'B'C'D'),(BCC'B'),(DCC'D'). Tính bán kính của (S).

A. $\frac{2 + \sqrt{3}}{3}$
B. $3 - \sqrt{3}$
C. $\frac{2 \sqrt{3}}{3}$
D. $\sqrt{2}$
Câu 677 : Cho số phức z thỏa mãn $(3 - 4 i) z - \frac{4}{|z|} = 8$ . Trên mặt phẳng tọa độ, khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z thuộc tập nào?

A. $(\frac{9}{4}; + \infty)$
B. $(\frac{1}{4}; \frac{5}{4})$
C. $(0; \frac{1}{4})$
D. $(\frac{1}{2}; \frac{9}{4})$

Câu 678 : Có tất cả bao nhiêu cặp số thực (x;y) sao cho $x \in [- 1; 1]$ và $\ln {(x - y)}^{x} - 2017 y + e^{2018}$ . Biết rằng giá trị lớn nhất của biểu thức $P = e^{2018} (y + 1) x^{2} - 2018 x^{2}$ với $(x; y) \in S$ đạt được tại $(x_{0}; y_{0})$ . Mệnh đề nào sau đây đúng?

A. $x_{0} \in (- 1; 0)$
B. $x_{0} = - 1$
C. $x_{0} = 1$
D. $x_{0} \in [0; 1)$
Câu 679 : Cho hàm số $y = x^{3} + 3 x^{2} - 2$ . Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số đồng biến trên khoảng $(- \infty; - 2) v à (0; + \infty)$
B. Hàm số nghịch biến trên khoảng $(- \infty; - 2) v à (0; + \infty)$
C. Hàm số đồng biến trên khoảng $(- \infty; 0) v à (2; + \infty)$
D. Hàm số nghịch biến trên khoảng $(- 2; 1)$
Câu 680 : Tìm khẳng định sai trong các khẳng định sau:

A. $\lim_{x \to - 2} (\sqrt{x^{2} + 5} - 3) = 0$
B. $\lim_{x \to - \infty} (- 3 x^{3} + 2 x + 5) = - \infty$
C. $\lim_{x \to + \infty} (x^{2} + 2 x + 3) = + \infty$
D. $\lim_{x \to 2} \frac{2 x + 3}{x - 1} = 7$
Câu 681 : Một vật chuyển động với quãng đường biến thiên theo thời gian được xác định bởi phương trình: $S (t) = t^{3} + 2 t^{2}$ (S tính bằng mét (m), t tính bằng giây (s)). Tính vận tốc của vật tại thời điểm vật chuyển động được quãng đường là 16m.

A. $v = 16 m / s$
B. $v = 7 m / s$
C. $v = 39 m / s$
D. $v = 20 m / s$

Câu 682 : Cho dãy số $(u_{n})$ với $\{\begin{array}{l} u_{1} = 10 \\ u_{n + 1} = \frac{1}{5} u_{n} + 3 \end{array}, \forall n \in N *$ . Tính $l i m u_{n}$

A. $l i m u_{n} = \frac{13}{4}$
B. $l i m u_{n} = 3$
C. $l i m u_{n} = \frac{15}{4}$
D. $l i m u_{n} = 2$
Câu 683 : Cho biểu thức $A = {(x + 2 y)}^{50}$ . Số hạng thứ 31 trong khai triển Newton của A là

A. $2^{19} C_{50}^{31} x^{31} y^{19}$
B. $2^{31} C_{50}^{31} x^{19} y^{31}$
C. $2^{30} C_{50}^{30} x^{20} y^{30}$
D. $2^{20} C_{50}^{30} x^{30} y^{20}$
Câu 684 : Cho x, y là các số thực dương thỏa mãn $9 \ln^{2} x + 4 \ln^{2} y = 12 \ln x . \ln y$ . Đẳng thức nào sau đây là đúng?

A. $x^{2} = y^{3}$
B. 3x = 2y
C. $x^{3} = y^{2}$
D. x = y
Câu 685 : Gọi $z_{1}, z_{2}$ là hai nghiệm phức của phương trình $z^{2} + 2 z + 10 = 0$ . Tính giá trị của biểu thức $A = {|z_{1}|}^{2} + {|z_{2}|}^{2}$

A. 15
B. 17
C. 19
D. 20

Câu 686 : Cho $f (x) = \sin^{5} a x, a > 0$ . Tính $f' (π)$

A. $f' (π) = 5 \sin^{4} (a π) . \cos (a π)$
B. $f' (π) = 0$
C. $f' (π) = 5 a . \sin^{4} (a π) . \cos (a π)$
D. $f' (π) = 5 a \sin^{4} (a π)$
Câu 687 : Cho hình lập phương $A B C D . A_{1} B_{1} C_{1} D_{1}$ . Gọi O là tâm của hình lập phương. Chọn đẳng thức đúng?

A. $\vec{A O} = \frac{1}{4} (\vec{A B} + \vec{A D} + \vec{A A_{1}})$
B. $\vec{A O} = \frac{2}{3} (\vec{A B} + \vec{A D} + \vec{A A_{1}})$
C. $\vec{A O} = \frac{1}{2} (\vec{A B} + \vec{A D} + \vec{A A_{1}})$
D. $\vec{A O} = \frac{1}{3} (\vec{A B} + \vec{A D} + \vec{A A_{1}})$
Câu 688 : Tìm số phức z thỏa mãn: $(2 - i) (1 + i) + \bar{z} = 4 - 2 i$

A. $z = - 1 - 3 i$
B. $z = - 1 + 3 i$
C. $z = 1 - 3 i$
D. $z = 1 + 3 i$
Câu 689 : Giá trị nhỏ nhất của hàm số $y = 2^{|x|}$ trên đoạn [-1;1] là

A. 2
B. 1
C. $\frac{1}{2}$
D. 4

Câu 690 : Đặt $\log_{3} 15 = m$ . Hãy biểu diễn $\log_{25} 15$ theo m:

A. $\log_{25} 15 = \frac{m}{m + 1}$
B. $\log_{25} 15 = \frac{m}{2 (m + 1)}$
C. $\log_{25} 15 = \frac{m}{m - 1}$
D. $\log_{25} 15 = \frac{m}{2 (m - 1)}$
Câu 691 : Tìm tất cả các giá trị của m để phương trình: 2sinx + mcosx - 2m = 0 có nghiệm?

A. $[\begin{array}{l} m \geq \frac{2}{\sqrt{3}} \\ m \leq - \frac{2}{\sqrt{3}} \end{array}$
B. $(- \frac{2}{\sqrt{3}}; \frac{2}{\sqrt{3}})$
C. $[- \frac{2}{\sqrt{3}}; \frac{2}{\sqrt{3}}]$
D. $m \in ℝ$
Câu 692 : Cho số phức z thỏa mãn: $\bar{z} = \frac{{(1 - \sqrt{3} i)}^{3}}{1 - i}$ . Tìm môđun của $\bar{z} + i z$

A. $8 \sqrt{2}$
B. $8 \sqrt{3}$
C. $4 \sqrt{2}$
D. $4 \sqrt{3}$
Câu 693 : Chọn khẳng định sai trong các mệnh đề sau?

A. $\log_{a} (b_{1} b_{2}) = \log_{a} b_{1} + \log_{a} b_{2}$
B. $a^{\log_{a}^{b}} = b$
C. $\log_{a} b = α \Leftrightarrow b^{α} = a$
D. $\log_{a} 1 = 0$

Câu 694 : Giá trị lớn nhất của hàm số $y = \ln x + \frac{1}{x}$ trên đoạn $[e; e^{2}]$ là:

A. $1 + \frac{1}{e}$
B. 2
C. $2 + \frac{1}{e^{2}}$
D. $e^{2} + 1$
Câu 695 : Một cái nón lá có chiều dài đường sinh và có đường kính mặt đáy đều bằng 5 dm. Vậy cần diện tích của lá để làm cái nón lá là:

A. $\frac{25 π}{6} d m^{2}$
B. $\frac{25 π}{4} d m^{2}$
C. $\frac{25 π}{2} d m^{2}$
D. $25 π d m^{2}$
Câu 696 : Cho một khối lập phương biết rằng khi giảm độ dài cạnh của khối lập phương thêm 4 cm thì thể tích của nó giảm bớt 604 $c m^{3}$ . Hỏi cạnh của khối lập phương đã cho bằng:

A. 10 cm
B. 9 cm
C. 7 cm
D. 8 cm
Câu 697 : Phương trình tiếp tuyến với đồ thị hàm số $y = f (x) = x^{3} - 3 x^{2} + 2$ tại điểm có hoành độ thỏa mãn $f'' (x) = 0$ là:

A. y = -x + 1
B. y = -3x + 3
C. y = -x - 1
D. y = -3x - 3

Câu 698 : Kết quả rút gọn của biểu thức $A = \log_{\frac{1}{3}} 7 + 2 \log_{9} 49 - \log_{\sqrt{3}} \frac{1}{7}$ là?

A. $\log_{7} 3$
B. $3 \log_{7} 3$
C. $\log_{3} 7$
D. $3 \log_{3} 7$
Câu 699 : Tập xác định của hàm số $y = \frac{\tan 2 x}{\cos x}$ ?

A. $D = ℝ$
B. $D = ℝ \ \{\frac{π}{4} + k \frac{π}{2}; \frac{π}{2} + k π\}, k \in ℤ$
C. $x \neq \frac{π}{4} + k \frac{π}{2}; x \neq \frac{π}{2} + k π, k \in ℤ$
D. $D = ℝ \ \{\frac{π}{2} + kπ\}, k \in ℤ$
Câu 700 : Cho hàm số u = u(x) có đạo hàm trên $ℝ$ . Khẳng định nào sau đây là đúng

A. $[u^{n} (x)]' = n . u^{n - 1} (x) . u' (x)$
B. $(\sqrt{u (x)})' = \frac{1}{2 \sqrt{u (x)}}, (u (x) > 0, \forall x \in ℝ)$
C. $[u^{n} (x)]' = n . u^{n - 1} (x)$
D. $(\sqrt{u (x)})' = \frac{u' (x)}{\sqrt{u (x)}}, (u (x) > 0, \forall x \in ℝ)$
Câu 701 : Phương trình tiếp tuyến của đồ thị hàm số $y = \frac{3 x + 2}{x - 2}$ tại điểm M(0;-1) là

A. y = -2x - 1
B. y = -2x + 1
C. y = -x - 1
D. y = -x + 1

Câu 702 : Trong các giới hạn sau, giới hạn nào không tồn tại?

A. $\lim_{x \to \infty} \frac{2 x + 1}{x^{2} + 1}$
B. $\lim_{x \to 0} \frac{x}{\sqrt{x + 1}}$
C. $\lim_{x \to 1} \frac{x}{{(x + 1)}^{2}}$
D. $\lim_{x \to 0} \frac{1}{x}$
Câu 703 : Xét f(x) là một hàm số tùy ý. Khẳng định nào sau đây là khẳng định đúng?

A. Nếu f(x) có đạo hàm tại $x_{0}$ và đạt cực đại tại $x_{0}$ thì $f' (x_{0}) = 0$
B. Nếu $f' (x_{0}) = 0$ thì f(x) đạt cực trị tại $x = x_{0}$
C. Nếu $f' (x_{0}) = 0$ và $f'' (x_{0}) > 0$ thì f(x) đạt cực trị tại $x = x_{0}$
D. Nếu f(x) đạt cực tiểu tại $x = x_{0}$ thì $f'' (x_{0}) > 0$
Câu 704 : Một máy bơm nước có ống bơm hình trụ đường kính bằng 50 cm và tốc độ dòng nước chảy trong ống là 0, 5 m/s. Hỏi trong một giờ máy bơm đó bơm được bao nhiêu nước? (giả sử nước lúc nào cũng đầy ống).

A. $\frac{225 π}{6} (m^{3})$
B. $225 π (m^{3})$
C. $450 π$
D. $\frac{225 π}{2} (m^{3})$
Câu 705 : Tìm giá trị thực của a để đẳng thức $\int_{0}^{a} \cos (x + a^{2}) d x = \sin a$ xảy ra ?

A. $a = \sqrt{3 π}$
B. $a = \sqrt{2 π}$
C. $a = π$
D. $a = \sqrt{π}$

Câu 706 : Các giá trị của tham số m để hàm số $y = x^{3} - 3 m x^{2} - 2 x - m$ nghịch biến trên khoảng (0;1) là

A. $m \geq 2$
B. $m \leq - 2$
C. $m \leq 0$
D. $m \geq \frac{1}{6}$
Câu 707 : Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn $|z - i| = |(1 + i) z|$

A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(2;-1) bán kính $R = \sqrt{2}$
B. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0;1) bán kính $R = \sqrt{3}$
C. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0;-1) bán kính $R = \sqrt{3}$
D. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0;-1) bán kính $R = \sqrt{2}$
Câu 708 : Với hai số thực dương a, b tùy ý và $\frac{\log_{3} 5 . \log_{5} a}{1 + \log_{3} 2} - \log_{6} b = 2$ . Khẳng định nào dưới đây là khẳng định đúng?

A. $a = b \log_{6} 2$
B. $a = 36 b$
C. 2a + 3b = 0
D. $a = b \log_{6} 3$
Câu 709 : Quả bóng đá được dùng thi đấu tại các giải bóng đá Việt Nam tổ chức có chu vi

A. $\approx$ 40 (miếng da).
B. $\approx$ 20(miếng da)
C. $\approx$ 35(miếng da)
D. $\approx$ 30(miếng da)

Câu 710 : Cho hàm số $f (x) = \log_{2} x, g (x) = 2^{x}$ . Xét các mệnh đề sau:

A. 2
B. 3
C. 1
D. 4
Câu 711 : Một người gửi số tiền 100 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền sẽ được nhập vào vốn ban đầu (người ta gọi đó là lãi kép). Để người đó lãnh được số tiền 250 triệu thì người đó cần gửi trong khoảng thời gian bao nhiêu năm ? (nếu trong khoảng thời gian này không rút tiền ra và lãi suất không thay đổi)

A. 12 năm
B. 13 năm
C. 14 năm
D. 15 năm
Câu 712 : Trung tâm trải nghiệm sáng tạo trường THPT XXX dự định xây một hồ chứa nước dạng hình hộp chữ nhật không có nắp có thể tích $V = \frac{500}{3} m^{3}$ đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thầu nhân công để xây hồ là 600000 đồng $/ m^{2}$ . Chi phí thuê nhân công nhỏ nhất bằng:

A. 80 triệu đồng
B. 90 triệu đồng
C. 100 triệu đồng
D. 75 triệu đồng
Câu 713 : Tìm m để phương trình: $|x^{3} - 3 x + 2| = \log_{\sqrt[4]{2}} (m^{2} + 1)$ có 4 nghiệm thực phân biệt.

A. $|m| \geq 1$
B. $|m| \leq 1$
C. $\{\begin{cases} |m| \leq 1 \\ m \neq 0 \end{cases}$
D. $|m| < 1$

Câu 714 : Xét hai số thực x, y thỏa mãn $x^{2} + y^{2} = 2$ . Tìm giá trị lớn nhất M của biểu thức $P = 2 (x^{3} + y^{3}) - 3 x y$

A. $M = \frac{11}{2}$
B. $M = \frac{13}{2}$
C. $M = \frac{15}{2}$
D. $M = \frac{17}{2}$
Câu 715 : Cho hình lập phương có cạnh bằng 40cm và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi $S_{1}, S_{2}$ lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình trụ. Tính $S = S_{1} + S_{2} (c m^{2})$

A. $S = 4 (2400 + π)$
B. $S = 2400 (4 + 2 π)$
C. $S = 2400 (4 + 3 π)$
D. $S = 4 (2400 + 3 π)$
Câu 716 : Cho hình chóp S.ABC có M,N lần lượt là trung điểm của SA,SB. Giao tuyến của hai mặt phẳng (CMN) và (SBC) là:

A. CN
B. SC
C. MN
D. CM

Đáp án có ở chi tiết câu hỏi nhé!!! (click chuột vào câu hỏi).

Thi đại học Toán học Thi đại học - Toán học

Xem thêm