Đăng nhập Đăng ký

Đăng nhập hoặc đăng ký miễn phí để đặt câu hỏi và nhận câu trả lời sớm nhất !

Đăng nhập
hoặc
Đăng kí

Tiểu học
Công thức
Đề thi & kiểm tra
Phương trình hóa học
Tuyển sinh
Review Sách
Review Ứng dụng

Tiểu học
Công thức
Đề thi & kiểm tra
Phương trình hóa học
Tuyển sinh
Review Sách
Review Ứng dụng

Liên hệ

102, Thái Thịnh, Trung Liệt, Đống Đa, Hà Nội

[email protected]

082346781

Trang chủ Đề thi & kiểm tra Lớp 12 Toán học 80 câu trắc nghiệm Khối đa diện nâng cao !!

80 câu trắc nghiệm Khối đa diện nâng cao !!

Câu 1 : Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, $\hat{B A C} = 120^{o}$ và BC =AA' = a $\sqrt{3}$ . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'.

A. $V = \frac{9 a^{3}}{4}$
B. $V = \frac{3 \sqrt{3} a^{3}}{6}$
C. $V = \frac{3 \sqrt{3} a^{3}}{2}$
D. $V = \frac{3 a^{3}}{4}$

Câu 2 : Cho khối lăng trụ tam giác đứng ABC.A'B'C' có đáy là tam giác vuông tại A, AC = AB = 2a, góc giữa AC' và mặt phẳng (ABC) bằng 30⁰. Tính thể tích của khối lăng trụ ABC.A'B'C'.

A. $\frac{2 \sqrt{3} a^{3}}{3}$
B. $\frac{\sqrt{3} a^{3}}{3}$
C. $\frac{a^{3}}{\sqrt{3}}$
D. $\frac{4 \sqrt{3} a^{3}}{3}$
Câu 3 : Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 45⁰.

A. $\frac{a^{3} \sqrt{3}}{4}$
B. $\frac{a^{3} \sqrt{3}}{12}$
C. $\frac{a^{3} \sqrt{2}}{12}$
D. $\frac{a^{3} \sqrt{2}}{4}$
Câu 4 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh $a \sqrt{3}$ . Cạnh bên SA vuông góc với mặt phẳng (ABCD) và SC=4a. Tìm thể tích khối chóp S.ABCD.

A. 3a³ $\sqrt{13}$
B. 3a³ $\sqrt{10}$
C. a³ $\sqrt{13}$
D. a³ $\sqrt{10}$
Câu 5 : Cho khối chóp S.ABCD có đáy là hình chữ nhật cạnh AB=3a, BC=a. Cạnh bên SA vuông góc với đáy; SC tạo với mặt phẳng (ABCD) một góc 60⁰. Tính thể tích V của khối chóp đã cho.

A. V = $\sqrt{60}$ a³
B. V = 3 $\sqrt{20}$ a³
C. V = $\sqrt{30}$ a³
D. V = 3a³.

Câu 6 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SO tạo với mặt phẳng đáy một góc 45⁰. Tính thể tích V của khối chóp S.ABCD.

A. $\frac{a^{3} \sqrt{2}}{2}$
B. $\frac{a^{3} \sqrt{2}}{3}$
C. $\frac{a^{3} \sqrt{2}}{6}$
D. $a^{3} \sqrt{2}$
Câu 7 : Cho hình lăng trụ ABC.A'B'C' có ABC là tam giác vuông tại A. Hình chiếu của A' lên (ABC) là trung điểm của BC. Tính thể tích V của khối lăng trụ ABC.A'B'C' biết AB=a, AC = $a \sqrt{3}$ , AA'=2a.

A. $\frac{3 a^{3}}{2}$
B. $a^{3} \sqrt{3}$
C. $3 a^{3} \sqrt{3}$
D. $\frac{a^{3} \sqrt{39}}{12}$
Câu 8 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy, SA=a. Gọi M là điểm nằm trên cạnh CD. Tính thể tích khối chóp S.ABM.

A. $\frac{a^{3}}{2}$
B. $a^{3}$
C. $\frac{a^{3}}{6}$
D. $\frac{3 a^{3}}{4}$
Câu 9 : Tính thể tích V của khối chóp S.ABC có đáy ABC là tam giác vuông tại A, AB=3a, BC=5a, SA = 2a $\sqrt{3}$ , $\hat{S A C} = 30^{o}$ và mặt phẳng (SAC) vuông góc mặt đáy.

A. $V = 3 a^{3} \sqrt{2}$
B. $V = \frac{a^{3} \sqrt{3}}{3}$
C. $V = a^{3} \sqrt{3}$
D. $V = 2 a^{3} \sqrt{3}$

Câu 10 : Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA=a và SA vuông góc với đáy. Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho SN=2ND. Tính thể tích V của khối tứ diện ACMN.

A. $V = \frac{1}{12} a^{3}$
B. $V = \frac{1}{6} a^{3}$
C. $V = \frac{1}{8} a^{3}$
D. $V = \frac{1}{36} a^{3}$
Câu 11 : Cho khối chóp S. ABC có $\hat{A S B} = \hat{B S C} = \hat{C S A} = 60^{o}$ , SA=a, SB=2a, SC=4a. Tính thể tích khối chóp S. ABC theo a.

A. $\frac{8 a^{3} \sqrt{2}}{3}$
B. $\frac{2 a^{3} \sqrt{2}}{3}$
C. $\frac{4 a^{3} \sqrt{2}}{3}$
D. $\frac{a^{3} \sqrt{2}}{3}$
Câu 12 : Cho hình chóp S. ABC có đáy là tam giác ABC đều cạnh a, tam giác SBA vuông tại B, tam giác SAC vuông tại C. Biết góc giữa hai mặt phẳng (SAB) và (ABC) bằng $60^{o}$ . Tính thể tích khối chóp S.ABC theo a.

A. $\frac{\sqrt{3} a^{3}}{8}$
B. $\frac{\sqrt{3} a^{3}}{12}$
C. $\frac{\sqrt{3} a^{3}}{6}$
D. $\frac{\sqrt{3} a^{3}}{4}$
Câu 13 : Cho hình chóp S. ABC có đáy là tam giác ABC vuông tại A góc $\hat{A B C} = 30^{o}$ ; tam giác SBC là tam giác đều cạnh a và mặt phẳng (SAB) vuông góc mặt phẳng (ABC). Khoảng cách từ A đến mặt phẳng (SBC) là:

A. $\frac{a \sqrt{6}}{5}$
B. $\frac{a \sqrt{6}}{3}$
C. $\frac{a \sqrt{3}}{3}$
D. $\frac{a \sqrt{6}}{6}$

Câu 14 : Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật với AB = a, BC = a $\sqrt{3}$ . Cạnh bên SA vuông góc với đáy và đường thẳng SC tạo với mặt phẳng (SAB) một góc 30 độ. Tính thể tích V của khối chóp S.ABCD theo a.

A. $V = \frac{2 \sqrt{6} a^{3}}{3}$
B. $V = \frac{2 a^{3}}{3}$
C. $V = \sqrt{3} a^{3}$
D. $V = \frac{\sqrt{3} a^{3}}{3}$
Câu 15 : Cho hình chóp S. ABCD có đáy ABCD là hình thoi và có thể tích bằng 2. Gọi M, N lần lượt là các điểm trên cạnh SB và SD sao cho $\frac{S M}{S B} = \frac{S N}{S D} = k$ . Tìm giá trị của k để thể tích khối chóp S.AMN bằng $\frac{1}{8}$

A.k = $\frac{1}{8}$
B.k = $\frac{\sqrt{2}}{2}$
C.k = $\frac{\sqrt{2}}{4}$
D.k = $\frac{1}{4}$
Câu 16 : Cho khối tứ diện ABCD có thể tích V và điểm E trên cạnh AB sao cho AE = 3EB. Tính thể tích khối tứ diện EBCD theo V.

A. $\frac{V}{4}$
B. $\frac{V}{3}$
C. $\frac{V}{2}$
D. $\frac{V}{5}$
Câu 17 : Cho hình tứ diện đều ABCD có cạnh bằng 3. Gọi G₁, G₂, G₃, G₄ lần lượt là trọng tâm của bốn mặt của tứ diện ABCD. Tính thể tích V của khối tứ diện G₁G₂G₃G₄.

A. $\frac{\sqrt{2}}{4}$
B. $\frac{\sqrt{2}}{18}$
C. $\frac{9 \sqrt{2}}{32}$
D. $\frac{\sqrt{2}}{12}$

Câu 18 : Cho hình chóp đều S. ABCD có AC = 2a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABCD) bằng 45⁰. Tính thể tích V của khối chóp S.ABCD theo a.

A. $V = \frac{a^{3} \sqrt{2}}{3}$
B. $V = \frac{2 a^{3} \sqrt{3}}{3}$
C. $V = a^{3} \sqrt{2}$
D. $V = \frac{a^{3}}{2}$
Câu 19 : Cho khối lăng trụ đứng, mặt phẳng (P) đi qua C' và các trung điểm của AA', BB' chia khối lăng trụ ABC. A'B'C' thành hai khối đa diện có tỷ số thể tích bằng k với k ≤ 1. Tìm k.

A. $\frac{1}{3}$
B. $\frac{2}{3}$
C. 1
D. $\frac{1}{2}$
Câu 20 : Cho khối chóp S. ABC có góc $\hat{A S B} = \hat{B S C} = \hat{C S A} = 60^{o}$ và SA=2, SB=3, SC=4. Thể tích khối chóp S. ABC.

A. $2 \sqrt{2}$
B. $2 \sqrt{3}$
C. $4 \sqrt{3}$
D. $3 \sqrt{2}$
Câu 21 : Hình lăng trụ ABC. A'B'C' có đáy ABC là tam giác vuông tại A; AB=1; AC=2. Hình chiếu vuông góc của A' trên (ABC) nằm trên đường thẳng BC. Tính khoảng cách từ điểm A đến mặt phẳng (A'BC).

A. $\frac{\sqrt{3}}{2}$
B. $\frac{1}{3}$
C. $\frac{2 \sqrt{5}}{5}$
D. $\frac{2}{3}$

Câu 22 : Cho khối lăng trụ ABC. A'B'C' có thể tích bằng 2018. Gọi M là trung điểm AA' ; N, P lần lượt là các điểm nằm trên các cạnh BB', CC' sao cho BN=2B'N, CP=3C'P. Tính thể tích khối đa diện ABC. MNP.

A. $\frac{32288}{27}$
B. $\frac{40360}{27}$
C. $\frac{4036}{3}$
D. $\frac{23207}{18}$
Câu 23 : Cho khối tứ diện ABCD có thể tích 2017. Gọi M, N, P, Q lần lượt là trọng tâm của các tam giác ABC, ABD, ACD, BCD. Tính thể tích của khối tứ diện MNPQ.

A. $\frac{2017}{9}$
B. $\frac{4034}{81}$
C. $\frac{8068}{27}$
D. $\frac{2017}{27}$
Câu 24 : Cho hình lăng trụ ABC. A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và BC bằng $\frac{a \sqrt{3}}{4}$ . Tính theo a thể tích V của khối lăng trụ ABC. A'B'C'.

A. $\frac{a^{3} \sqrt{3}}{6}$
B. $\frac{a^{3} \sqrt{3}}{12}$
C. $\frac{a^{3} \sqrt{3}}{3}$
D. $\frac{a^{3} \sqrt{3}}{24}$
Câu 25 : Cho hình lăng trụ đứng ABC. A'B'C', biết đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A'BC) bằng $\frac{a}{6}$ . Tính thể tích khối lăng trụ ABC. A'B'C'.

A. $\frac{3 a^{3} \sqrt{2}}{8}$
B. $\frac{3 a^{3} \sqrt{2}}{28}$
C. $\frac{3 a^{3} \sqrt{2}}{4}$
D. $\frac{3 a^{3} \sqrt{2}}{16}$

Câu 26 : Cho khối tứ diện ABCD có thể tích bằng V, thể tích của khối đa diện có đỉnh là trung điểm các cạnh của tứ diện ABCD bằng V'. Tính tỉ số V'/V.

A. $\frac{V'}{V} = \frac{1}{2}$
B. $\frac{V'}{V} = \frac{1}{8}$
C. $\frac{V'}{V} = \frac{1}{4}$
D. $\frac{V'}{V} = \frac{3}{4}$
Câu 27 : Cho khối chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD). Góc giữa mặt phẳng (SBC) và (ABCD) bằng $45^{o}$ . Gọi M, N lần lượt là trung điểm AB, AD. Tính thể tích khối chóp S. CDMN theo a.

A. $\frac{5 a^{3}}{8}$
B. $\frac{a^{3}}{8}$
C. $\frac{5 a^{3}}{24}$
D. $\frac{a^{3}}{3}$
Câu 28 : Cho hình chóp tam giác S. ABC có đáy ABC là tam giác đều cạnh a, SA=a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A. BCNM bằng:

A. $\frac{a^{3} \sqrt{3}}{12}$
B. $\frac{a^{3} \sqrt{3}}{48}$
C. $\frac{a^{3} \sqrt{3}}{24}$
D. $\frac{a^{3} \sqrt{3}}{16}$
Câu 29 : Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng $60^{o}$ . Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD, DC. Thể tích khối tứ diện ACMN là:

A. $\frac{a^{3} \sqrt{2}}{4}$
B. $\frac{a^{3}}{8}$
C. $\frac{a^{3} \sqrt{3}}{6}$
D. $\frac{a^{3} \sqrt{2}}{2}$

Câu 30 : Cho tứ diện ABCD có AB = AD = a $\sqrt{2}$ , BC = BD = a và CA = CD = x. Khoảng cách từ B đến mặt phẳng (ACD) bằng $\frac{a \sqrt{3}}{2}$ . Biết thể tích của khối tứ diện bằng $\frac{a^{3} \sqrt{3}}{12}$ . Góc giữa hai mặt phẳng (ACD) và (BCD) là:

A.60⁰
B.45⁰
C.90⁰
D.120⁰
Câu 31 : Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng 2a. Mặt bên của hình chóp tạo với mặt đáy một góc 60⁰. Mặt phẳng (P) chứa AB và đi qua trọng tâm G của tam giác SAC cắt SC, SD lần lượt tại M và N. Thể tích khối chóp S. ABMN là:

A. $\frac{a^{3} \sqrt{3}}{2}$
B. $\frac{a^{3} \sqrt{3}}{4}$
C. $\frac{a^{3} \sqrt{3}}{3}$
D. $a^{3} \sqrt{3}$
Câu 32 : Cho hình chóp tứ giác S. ABCD đáy là hình bình hành có thể tích bằng V. Lấy điểm B', D' lần lượt là trung điểm của cạnh SB và SD. Mặt phẳng qua (AB'D') cắt cạnh SC tại C'. Khi đó thể tích khối chóp S. AB'C'D' bằng:

A. $\frac{V}{3}$
B. $\frac{2 V}{3}$
C. $\frac{V^{3}}{3}$
D. $\frac{V}{6}$
Câu 33 : Cắt khối hộp ABCD. A'B'C'D' bởi các mặt phẳng (AB'D'), (CB'D'), (B'AC), (D'AC) ta được khối đa diện có thể tích lớn nhất là:

A.A'CB'D'
B.A'C'BD
C.ACB'D'
D.AC'B'D'

Câu 34 : Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết $V_{S . A E F} = \frac{1}{4} V_{S . A B C}$ . Tính thể tích V của khối chóp S. ABC.

A. $\frac{a^{3}}{2}$
B. $\frac{a^{3}}{8}$
C. $\frac{2 a^{3}}{5}$
D. $\frac{a^{3}}{12}$
Câu 35 : Cho lăng trụ tam giác đều ABC. A'B'C' có cạnh đáy bằng a và $A B' ⊥ B C'$ . Tính thể tích V của khối lăng trụ đã cho.

A. $\frac{7 a^{3}}{8}$
B. $a^{3} \sqrt{6}$
C. $\frac{a^{3} \sqrt{6}}{8}$
D. $\frac{a^{3} \sqrt{6}}{4}$
Câu 36 : Cho hình lăng trụ đứng ABC. A'B'C' có đáy là tam giác vuông và AB=BC=a, AA' = $a \sqrt{2}$ , M là trung điểm của BC. Tính khoảng cách d của hai đường thẳng AM và B'C.

A. $d = \frac{a \sqrt{2}}{2}$
B. $d = \frac{a \sqrt{6}}{6}$
C. $d = \frac{a \sqrt{7}}{7}$
D. $d = \frac{a \sqrt{3}}{3}$
Câu 37 : Cho hình chóp S. ABCD có đáy là hình chữ nhật, AB = a, AD = a $\sqrt{2}$ . Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của BC, SH = $\frac{a \sqrt{2}}{2}$ . Tính bán kính mặt cầu ngoại tiếp hình chóp S. BHD.

A. $\frac{a \sqrt{2}}{2}$
B. $\frac{a \sqrt{5}}{2}$
C. $\frac{a \sqrt{17}}{4}$
D. $\frac{a \sqrt{11}}{4}$

Câu 38 : Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA = $\frac{a \sqrt{2}}{2}$ , OB=OC=a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). Tính thể tích khối tứ diện OABH.

A. $\frac{a^{3} \sqrt{2}}{6}$
B. $\frac{a^{3} \sqrt{2}}{12}$
C. $\frac{a^{3} \sqrt{2}}{24}$
D. $\frac{a^{3} \sqrt{2}}{48}$
Câu 39 : Cho hình lập phương ABCD. A'B'C'D' có cạnh bằng a. Gọi O và O' lần lượt là tâm các hình vuông ABCD và A'B'C'D'. Gọi M, N lần lượt là trung điểm của các cạnh B'C' và CD. Tính thể tích khối tứ diện OO'MN.

A. $\frac{a^{3}}{8}$
B. a³
C. $\frac{a^{3}}{12}$
D. $\frac{a^{3}}{24}$
Câu 40 : Xét khối lăng trụ tam giác ABC. A'B'C'. Mặt phẳng đi qua C' và các trung điểm của AA', BB' chia khối lăng trụ thành hai phần có tỉ số thể tích bằng:

A. $\frac{2}{3}$
B. $\frac{1}{2}$
C. 1
D. $\frac{1}{3}$
Câu 41 : Cho tứ diện OABC biết OA, OB, OC đôi một vuông góc với nhau, biết OA=3, OB=4 và thể tích khối tứ diện OABC bằng 6. Khi đó khoảng cách từ O đến mặt phẳng (ABC) bằng:

A. 3
B. $\frac{\sqrt{41}}{12}$
C. $\frac{144}{\sqrt{41}}$
D. $\frac{12}{\sqrt{41}}$

Câu 42 : Cho hình chóp tứ giác đều S. ABCD. Mặt phẳng (P) chứa đường thẳng AC và vuông góc với mặt phẳng (SCD), cắt đường thẳng SD tại E. Gọi V và V₁ lần lượt là thể tích các khối chóp S.ABCD và D.ACE. Tính số đo góc tạo bởi mặt bên và mặt đáy của hình chóp S.ABCD biết V = 5 $V_{1}$

A. 60⁰
B. 120⁰
C. 45⁰
D. 90⁰
Câu 43 : Cho hình chóp S. ABC, có AB=5 (cm), BC=6 (cm), AC=7 (cm). Các mặt bên tạo với đáy 1 góc 60⁰. Thể tích của khối chóp bằng:

A. $\frac{105 \sqrt{3}}{2}$ ( $c m^{3}$ )
B. $\frac{35 \sqrt{3}}{2} (c m^{3})$
C. $24 \sqrt{3} (c m^{3})$
D. $8 \sqrt{3} (c m^{3})$
Câu 44 : Cho khối lăng trụ tam giác đều ABC. A'B'C' có cạnh đáy là a và khoảng cách từ A đến mặt phẳng (A'BC) bằng a/2. Thể tích của khối lăng trụ bằng:

A. $\frac{3 \sqrt{2} a^{3}}{12}$
B. $\frac{\sqrt{2} a^{3}}{16}$
C. $\frac{3 a^{3} \sqrt{2}}{16}$
D. $\frac{3 a^{3} \sqrt{2}}{48}$
Câu 45 : Cho lăng trụ tam giác đều ABC. A'B'C' có tất cả các cạnh đều bằng a. Khoảng cách giữa hai đường thẳng BC và AB' bằng:

A. $\frac{a \sqrt{21}}{7}$
B. $\frac{a \sqrt{3}}{2}$
C. $\frac{a \sqrt{7}}{4}$
D. $\frac{a \sqrt{2}}{2}$

Câu 46 : Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA = a và SA vuông góc với đáy. Gọi M là trung điểm SB, N thuộc cạnh SD sao cho SN = 2ND. Tính thể tích V của khối tứ diện ACMN.

A. V = $\frac{1}{8} a^{3}$
B. V = $\frac{1}{6} a^{3}$
C. V = $\frac{1}{36} a^{3}$
D. V = $\frac{1}{12} a^{3}$
Câu 47 : Cho khối hộp chữ nhật ABCD. A'B'C'D' có thể tích bằng 2110. Biết (MNP), DN=3ND', CP=2C'P như hình vẽ. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằng:

A. $\frac{5275}{6}$
B. $\frac{8440}{9}$
C. $\frac{7485}{18}$
D. $\frac{5275}{12}$
Câu 48 : Xét tứ diện ABCD có các cạnh AB=BC=CD=DA=1 và AC, BD thay đổi. Giá trị lớn nhất của thể tích khối tứ diện ABCD bằng:

A. $\frac{2 \sqrt{3}}{27}$
B. $\frac{4 \sqrt{3}}{27}$
C. $\frac{2 \sqrt{3}}{9}$
D. $\frac{4 \sqrt{3}}{9}$
Câu 49 : Cho khối lăng trụ tam giác ABC. A'B'C'. Gọi M, N lần lượt là trung điểm của BB' và CC'. Mặt phẳng (AMN) chia khối lăng trụ thành hai phần. Gọi V₁ là thể tích của khối đa diện chứa đỉnh B' và V₂ là thể tích khối đa diện còn lại. Tính tỉ số V₁/V₂.

A. $\frac{V_{1}}{V_{2}} = \frac{7}{2}$
B. $\frac{V_{1}}{V_{2}} = 2$
C. $\frac{V_{1}}{V_{2}} = \frac{1}{3}$
D. $\frac{V_{1}}{V_{2}} = \frac{5}{2}$

Câu 50 : Xét tứ diện ABCD có các cạnh AC=CD=DB=BA=2 và AD, BC thay đổi. Giá trị lớn nhất của thể tích tứ diện ABCD bằng:

A. $\frac{16 \sqrt{3}}{9}$
B. $\frac{32 \sqrt{3}}{27}$
C. $\frac{16 \sqrt{3}}{27}$
D. $\frac{32 \sqrt{3}}{9}$
Câu 51 : Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy, AB = a, BC = $a \sqrt{2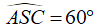}$ , SC=2a và . Tính bán kính R của mặt cầu ngoại tiếp tứ diện S.ABC

A. R = a
B. R = $\frac{a \sqrt{3}}{2}$
C. R = $a \sqrt{3}$
D. R = $\frac{a}{2}$
Câu 52 : Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, SC hợp với đáy một góc 30⁰, M là trung điểm của AC. Tính thể tích khối chóp S. BCM.

A. $\frac{\sqrt{3} a^{3}}{48}$
B. $\frac{\sqrt{3} a^{3}}{16}$
C. $\frac{\sqrt{3} a^{3}}{96}$
D. $\frac{\sqrt{3} a^{3}}{24}$
Câu 53 : Cho điểm M nằm trên cạnh SA, điểm N nằm trên cạnh SB của hình chóp tam giác S. ABC sao cho $\frac{S M}{M A} = \frac{1}{2}, \frac{S N}{N B} = 2$ . Mặt phẳng (α) qua MN và song song với SC chia khối chóp thành 2 phần. Gọi V₁ là thể tích của khối đa diện chứa A, V₂ là thể tích của khối đa diện còn lại. Tính tỉ số $\frac{V_{1}}{V_{2}}$

A. $\frac{V_{1}}{V_{2}} = \frac{4}{5}$
B. $\frac{V_{1}}{V_{2}} = \frac{5}{4}$
C. $\frac{V_{1}}{V_{2}} = \frac{5}{6}$
D. $\frac{V_{1}}{V_{2}} = \frac{6}{5}$

Câu 54 : Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, biết SC = $a \sqrt{3}$ . Gọi M, N, P, Q lần lượt là trung điểm các cạnh SB, SD, CD, BC. Tính thể tích khối chóp AMNPQ

A. $\frac{a^{3}}{3}$
B. $\frac{a^{3}}{4}$
C. $\frac{a^{3}}{8}$
D. $\frac{a^{3}}{12}$
Câu 55 : Cho hình chóp tứ giác đều S. ABCD, M là trung điểm của SC. Mặt phẳng (P) qua AM và song song với BD cắt SB, SD tại N, K. Tính tỉ số thể tích của khối S. ANMK và khối chóp S.ABCD.

A. $\frac{2}{9}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{3}{5}$
Câu 56 : Cho khối hộp ABCD. A'B'C'D' có đáy là hình chữ nhật với AB = $\sqrt{3}$ ; AD = $\sqrt{7}$ . Hai mặt bên (ABB'A') và (ADD'A') cùng tạo với đáy góc 45⁰, cạnh bên của hình hộp bằng 1 (hình vẽ). Thể tích khối hộp là:

A. $\sqrt{7}$
B. $3 \sqrt{3}$
C. 5
D. $7 \sqrt{7}$
Câu 57 : Cho hình chóp S. ABC có SA, SB, SC đôi một vuông góc với nhau và SA=SB=SC=a. Sin của góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:

A. $\frac{\sqrt{6}}{3}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{1}{\sqrt{3}}$
D. $\frac{2}{\sqrt{6}}$

Câu 58 : Cho tứ diện đều có cạnh bằng 3. M là một điểm thuộc miền trong của khối tứ diện tương ứng. Tính giá trị lớn nhất của tích các khoảng cách từ điểm M đến bốn mặt của tứ diện đã cho.

A. 36
B. 9/64
C. $\sqrt{6}$
D. $\frac{\sqrt{6}}{4}$
Câu 59 : Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Biết khoảng cách giữa hai đường thẳng BC và SM bằng $\frac{a \sqrt{3}}{4}$ . Tính thể tích của khối chóp đã cho theo a.

A. $\frac{a^{3} \sqrt{3}}{4}$
B. $\frac{a^{3} \sqrt{3}}{2}$
C. $\frac{a^{3} \sqrt{3}}{6}$
D. $\frac{a^{3} \sqrt{3}}{12}$
Câu 60 : Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và BC bằng a√3/4. Tính thể tích V của khối lăng trụ ABC.A'B'C'

A. V = $\frac{a^{3} \sqrt{3}}{6}$
B. V = $\frac{a^{3} \sqrt{3}}{3}$
C. V = $\frac{a^{3} \sqrt{3}}{24}$
D. V = $\frac{a^{3} \sqrt{3}}{12}$
Câu 61 : Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB = a, BC = 2a, BD = a $\sqrt{10}$ . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 60⁰. Tính thể tích V của khối chóp S.ABCD theo a.

A. V = $\frac{3 \sqrt{30} a^{3}}{8}$
B. V = $\frac{\sqrt{30} a^{3}}{4}$
C. V = $\frac{\sqrt{30} a^{3}}{12}$
D. V = $\frac{\sqrt{30} a^{3}}{8}$

Câu 62 : Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy (ABCD). Biết côsin của góc tạo bởi mặt phẳng (SCD) và (ABCD) bằng $\frac{2 \sqrt{17}}{17}$ . Thể tích Vcủa khối chóp S.ABCD là:

A. V = $\frac{a^{3} \sqrt{13}}{6}$
B. V = $\frac{a^{3} \sqrt{17}}{6}$
C. V = $\frac{a^{3} \sqrt{17}}{2}$
D. V = $\frac{a^{3} \sqrt{13}}{2}$
Câu 63 : Khối chóp S.ABCD có đáy là hình thoi cạnh a, SA = SB = SC = a, cạnh SD thay đổi. Thể tích lớn nhất của khối chóp S.ABCD là:

A. $\frac{a^{3}}{2}$
B. $\frac{a^{3}}{8}$
C. $\frac{3 a^{3}}{8}$
D. $\frac{a^{3}}{4}$
Câu 64 : Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Khoảng cách từ A đến mặt phẳng (A'BC) bằng:

A. $\frac{a \sqrt{2}}{2}$
B. $\frac{a \sqrt{3}}{4}$
C. $\frac{a \sqrt{21}}{7}$
D. $\frac{a \sqrt{6}}{4}$
Câu 65 : Hình lăng trụ đứng ABC.A'B'C' có diện tích đáy bằng 4, diện tích ba mặt bên lần lượt là 9, 18 và 10. Thể tích khối lăng trụ ABC.A'B'C' bằng:

A. $\sqrt[4]{11951}$
B. $\frac{\sqrt[4]{11951}}{2}$
C. $\sqrt{11951}$
D. $\frac{\sqrt{11951}}{2}$

Câu 66 : Cho hình lăng trụ ABC.A'B'C' có thể tích bằng 48cm³. Gọi M, N, P theo thứ tự là trung điểm các cạnh CC', BC và B'C', khi đó thể tích V của khối chóp A'.MNP là:

A.16/3 cm³
B.8cm³
C.24cm³
D. 12cm³
Câu 67 : Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AB = a. Gọi I là trung điểm của AC. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là điểm H thỏa mãn $\vec{B I}$ = 3 $\vec{I H}$ . Góc giữa hai mặt phẳng (SAB) và (SBC) là 60 độ. Thể tích của khối chóp S.ABC là:

A. V = a³/9
B.V = a³/6
C.V = a³/18
D.V = a³/3
Câu 68 : Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA = a $\sqrt{2}$ . Một mặt phẳng đi qua A vuông góc với SC cắt SB, SD, SC lần lượt tại B', D', C'. Thể tích khối chóp S. AB'C'D' là:

A. V = $\frac{2 a^{3} \sqrt{3}}{9}$
B. V = $\frac{2 a^{3} \sqrt{2}}{3}$
C. V = $\frac{a^{3} \sqrt{2}}{9}$
D. V = $\frac{2 a^{3} \sqrt{3}}{3}$
Câu 69 : Cho khối tứ diện đều ABCD có thể tích là V. Gọi M, N, P, Q lần lượt là trung điểm của AC, AD, BD, BC. Thể tích khối chóp AMNPQ là:

A. $\frac{V}{6}$
B. $\frac{V}{3}$
C. $\frac{V}{4}$
D. $\frac{V \sqrt{2}}{3}$

Câu 70 : Cho hình lăng trụ tam giác đều ABC. A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60⁰, cạnh AB=a. Tính thể tích V của khối lăng trụ ABC. A'B'C'.

A. V = $\frac{\sqrt{3}}{4} a^{3}$
B. V = $\frac{3}{4} a^{3}$
C. V = $\frac{3 \sqrt{3} a^{3}}{8}$
D. V = $\sqrt{3} a^{3}$
Câu 71 : Cho tứ diện SABC và hai điểm M, N lần lượt thuộc các cạnh SA, SB sao cho $\frac{S M}{A M} = \frac{1}{2}$ , $\frac{S N}{B N} = 2$ . Mặt phăng (P) đi qua hai điểm M, N và song song với cạnh SC, cắt AC, BC lần lượt tại L, K. Tính tỉ số thể tích $\frac{V_{S C M N K L}}{V_{S A B C}}$

A. $\frac{V_{S C M N K L}}{V_{S A B C}} = \frac{4}{9}$
B. $\frac{V_{S C M N K L}}{V_{S A B C}} = \frac{1}{3}$
C. $\frac{V_{S C M N K L}}{V_{S A B C}} = \frac{2}{3}$
D. $\frac{V_{S C M N K L}}{V_{S A B C}} = \frac{1}{4}$
Câu 72 : Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A'BC) bằng $\frac{a}{6}$ . Thể tích khối lăng trụ bằng

A. $\frac{3 a^{3} \sqrt{2}}{4}$
B. $\frac{3 a^{3} \sqrt{2}}{8}$
C. $\frac{3 a^{3} \sqrt{2}}{28}$
D. $\frac{3 a^{3} \sqrt{2}}{16}$
Câu 73 : Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a và cạnh bên SA vuông góc với mặt phẳng đáy. Gọi E là trung điểm của cạnh CD. Biết thể tích của khối chóp S. ABCD bằng $\frac{a^{3}}{3}$ . Tính khoảng cách từ A đến mặt phẳng (SBE).

A. $\frac{2 a}{3}$
B. $\frac{a \sqrt{2}}{3}$
C. $\frac{a}{3}$
D. $\frac{a \sqrt{3}}{3}$

Câu 74 : Cho khối chóp S. ABCD có đáy ABCD là tứ giác lồi, tam giác ABD đều cạnh a, tam giác BCD cân tại C và $\hat{B C D} = 120^{0}$ , $S A ⊥ (A B C D)$ và SA=a. Mặt phẳng (P) đi qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại M, N, P. Tính thể tích khối chóp S. AMNP.

A. $\frac{a^{3} \sqrt{3}}{42}$
B. $\frac{2 a^{3} \sqrt{3}}{21}$
C. $\frac{a^{3} \sqrt{3}}{14}$
D. $\frac{a^{3} \sqrt{3}}{12}$
Câu 75 : Cho khối chóp tứ giác S. ABCD. Mặt phẳng đi qua trọng tâm các tam giác SAB, SAC, SAD chia khối chóp này thành hai phần có thể tích là V₁ và V₂ (V₁ < V₂). Tính tỉ lệ V₁/V₂.

A. 8/27
B. 16/81
C. 8/19
D. 16/75
Câu 76 : Cho hình lăng trụ ABC. A'B'C' có đáy ABC là tam giác vuông tại A. cạnh BC=2a và $\hat{B' B C}$ nhọn. Biết (BCC'B') vuông góc với (ABC) và (ABB'A') tạo với (ABC) góc 45⁰. Thể tích của khối lăng trụ ABC. A'B'C' bằng:

A. $\frac{a^{3}}{\sqrt{7}}$
B. $\frac{3 a^{3}}{\sqrt{7}}$
C. $\frac{6 a^{3}}{\sqrt{7}}$
D. $\frac{a^{3}}{3 \sqrt{7}}$
Câu 77 : Cho khối lăng trụ ABC. A'B'C'. Gọi E là trọng tâm tam giác A'B'C' và F là trung điểm BC. Tính tỉ số thể tích giữa khối B'. EAF và khối lăng trụ ABC. A'B'C'.

A. $\frac{1}{4}$
B. $\frac{1}{8}$
C. $\frac{1}{5}$
D. $\frac{1}{6}$

Câu 78 : Cho hình chóp S. ABC có đường cao SA=2a, tam giác ABC vuông tại C, AB=2a, $\hat{C A B} = 30^{0}$ . Gọi H là hình chiếu của A trên SC, B' là điểm đối xứng của B qua mặt phẳng (SAC). Thể tích của khối chóp H. AB'B bằng:

A. $\frac{a^{3} \sqrt{3}}{7}$
B. $\frac{6 a^{3} \sqrt{3}}{7}$
C. $\frac{4 a^{3} \sqrt{3}}{7}$
D. $\frac{2 a^{3} \sqrt{3}}{7}$

Đáp án có ở chi tiết câu hỏi nhé!!! (click chuột vào câu hỏi).

Lớp 12 Toán học Lớp 12 - Toán học

Xem thêm

- Trắc nghiệm Toán 12 Chương 2 Bài 1 Lũy thừa
- Trắc nghiệm Toán 12 Chương 2 Bài 2 Hàm số lũy thừa
- Trắc nghiệm Toán 12 Chương 2 Bài 4 Hàm số mũ và hàm số lôgarit
- Trắc nghiệm Toán 12 Chương 2 Bài 5 Phương trình mũ và phương trình lôgarit
- Trắc nghiệm Toán 12 Chương 2 Bài 6 Bất phương trình mũ và bất phương trình lôgarit
- Trắc nghiệm Toán 12 Chương 3 Bài 1 Nguyên hàm
- Trắc nghiệm Toán 12 Chương 3 Bài 2 Tích phân
- Trắc nghiệm Toán 12 Chương 3 Bài 3 Ứng dụng của tích phân trong hình học
- Trắc nghiệm Toán 12 Bài 1 Số phức
- Trắc nghiệm Toán 12 Bài 2 Cộng, trừ và nhân số phức

Lớp 2 Lớp 3 Lớp 4 Lớp 5 Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12

Email: [email protected]

Giới thiệu

Về chúng tôi Điều khoản thỏa thuận sử dụng dịch vụ Câu hỏi thường gặp

Chương trình học

Hướng dẫn bài tập Giải bài tập Phương trình hóa học Thông tin tuyển sinh Đố vui

Địa chỉ: 102, Thái Thịnh, Trung Liệt, Đống Đa, Hà Nội

Email: [email protected]

Copyright © 2021 CungHocVui

Xem. Đặt câu hỏi. Trả lời.

Liên kết với Facebook

Liên kết với Google

hoặc

Ghi nhớ Quên mật khẩu?

Chưa có tài khoản?Đăng ký ngay!