Giải bài 1 trang 134 - Sách giáo khoa Toán 9 tập 2

Đề bài

   Chu vi hình chữ nhật ABCD là 20cm. Hãy tìm giá trị nhỏ nhất của độ dài đường chéo AC.

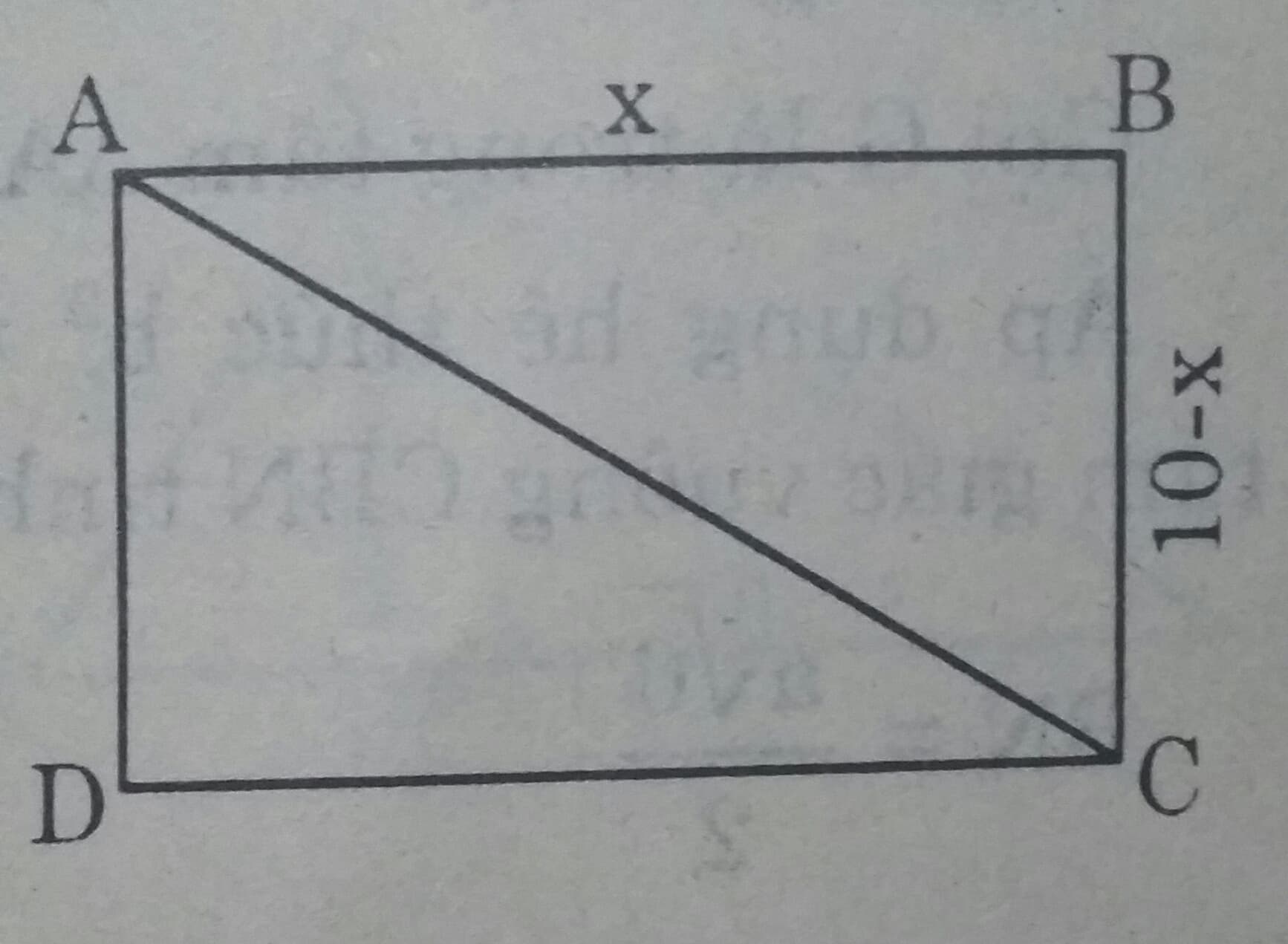
Hướng dẫn giải

   Đặt AB = x thì BC = 10- x

   Áp dụng định lý Pitago vào tam giác vuông ABC, ta được:

   \(AC^2 = AB^2 +BC^2 \\ AC^2 = x^2 + (10-x)^2 = 2x^2 - 20x + 100\\= 2(x^2- 10 + 50) = 2[(x-5)^2+ 25]\\= 2(x -5)^2 + 50 \\ Vì \ 2(x- 5)^2 \ge 0 \ nên \ AC^2 \ge 50 \Rightarrow AC \ge 5 \sqrt{2}\\\Rightarrow AC_{min} = 5 \sqrt{2}(cm) \Leftrightarrow x =5\)