Giải bài 11 trang 135 - Sách giáo khoa Toán 9 tập 2

Đề bài

   Từ một điểm P ở ngoài đường tròn (O), kẻ cát tuyến PAB và PCD tới đường tròn. Gọi Q là một điểm nằm trên cung nhỏ BD (không chứa A và C) sao cho:

Hướng dẫn giải

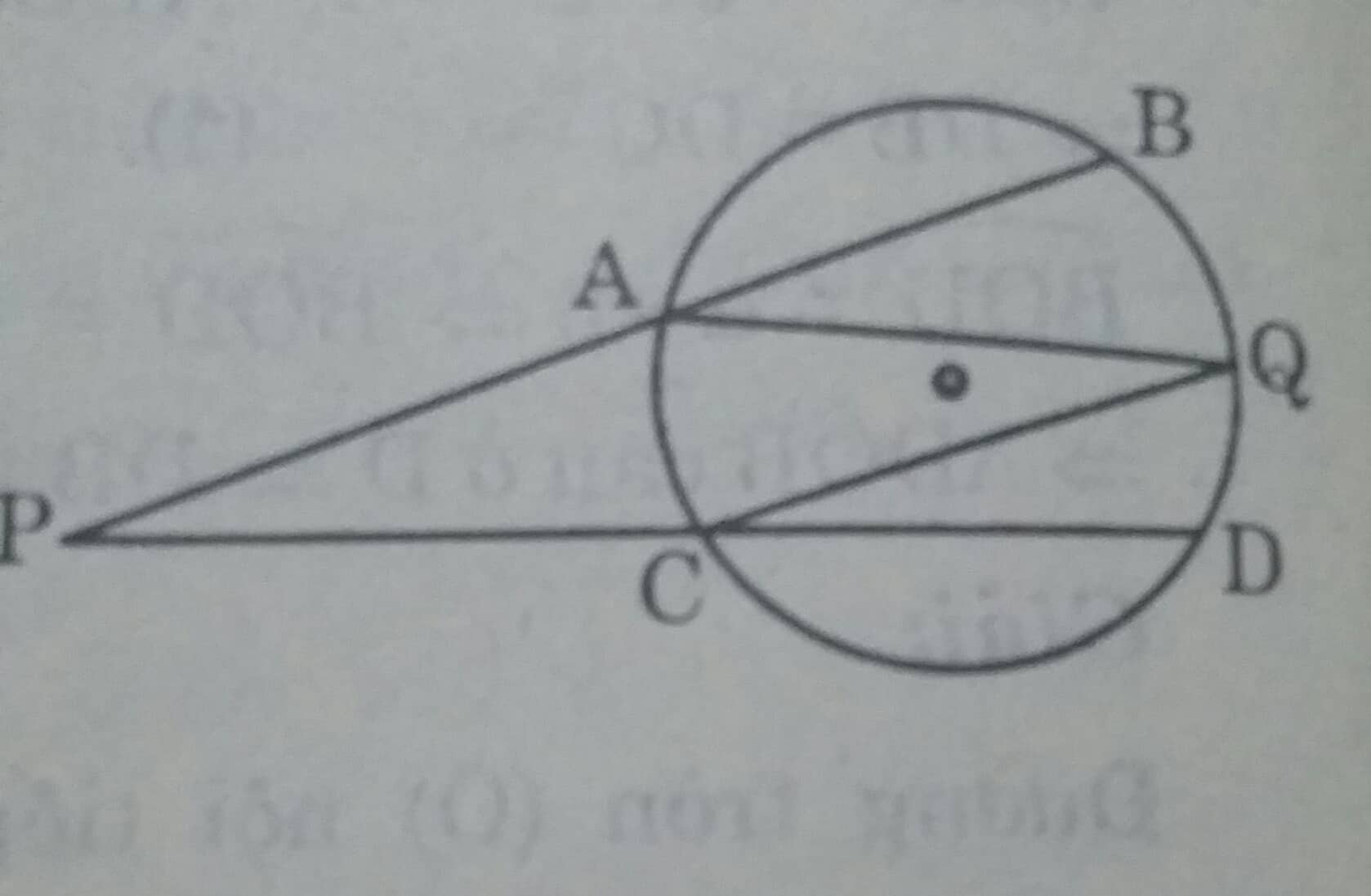
   Góc BPD là góc có đỉnh ở bên tròn đường tròn, nên: 

   \(\widehat{BPD} =\dfrac{sđ \stackrel\frown{BQD}+\stackrel\frown{AC}}{2}\)

   Góc AQC là góc nội tiếp nên:

   \(\widehat{AQC} =\dfrac{sđ \stackrel\frown{AC}}{2}\)

   Do đó  \(\widehat{BPD}+ \widehat{AQC} =- \dfrac{sđ \stackrel\frown{BQD} }{2}= \dfrac{42^0 + 38^ 0}{2}= 40^0\)