Giải bài 8 trang 134 - Sách giáo khoa Toán 9 tập 2

Đề bài

   Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài (R > r). Hai tiếp tuyến chung AB và A'B' của hai đường tròn (O),(O') cắt nhau tại P(A và A' thuộc đường tròn (O'), B và B' thuộc đường tròn (O)). Biết PA = AB = 4 cm. Tính diện tích hình tròn (O').

Hướng dẫn giải

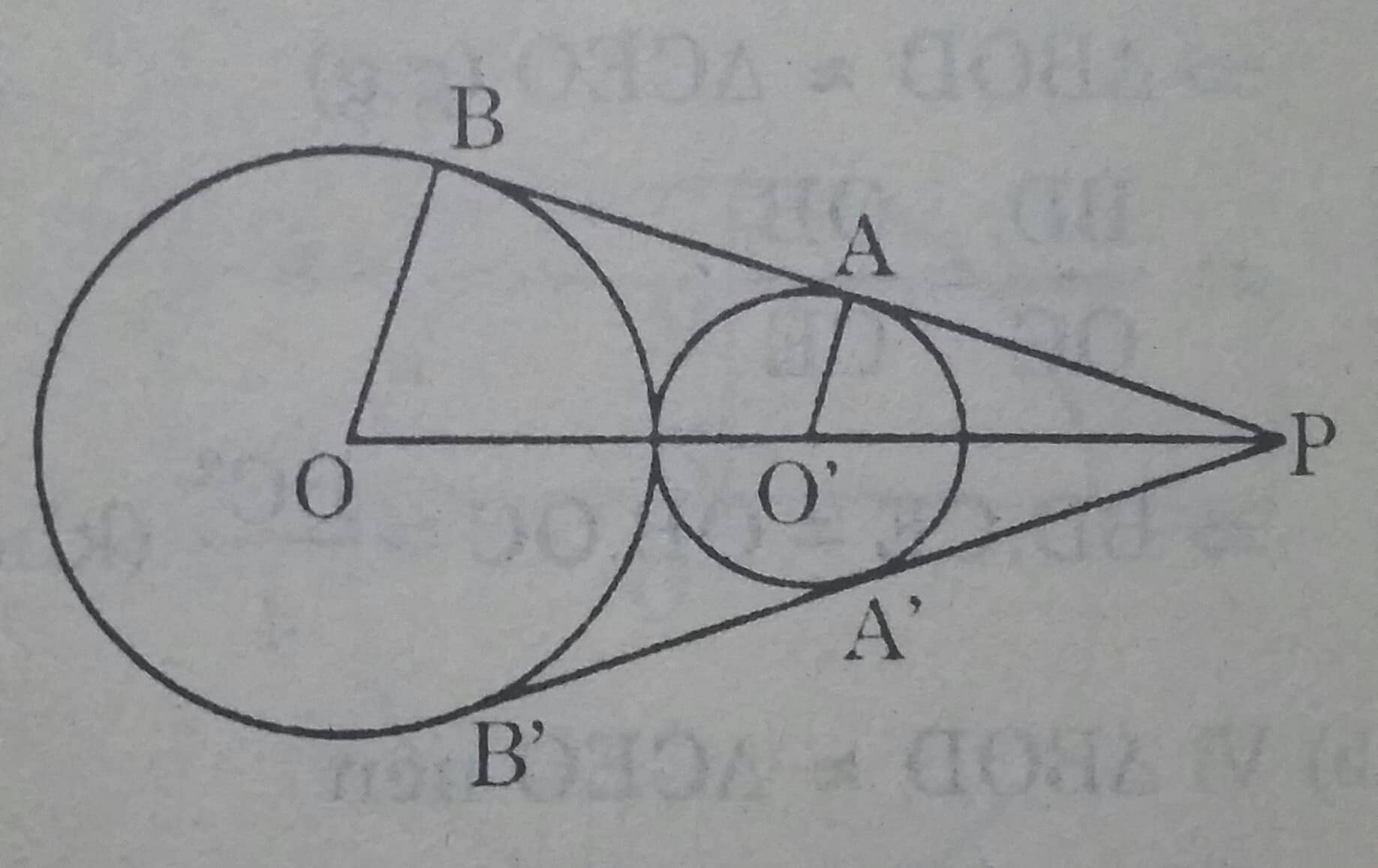
 Ta có AB là tiếp tuyến chung của hai đường tròn nên:

   O'A // Ob ( cùng vuông góc với AB)

   Điểm P là giao điểm của hai tiếp tuyến nên P nằm trên đường nối tâm.

   Xét \(\Delta POB \) có O'A //OB nên theo hệ quả của định lú Talet, ta có:

   \(\dfrac{O'A}{OB}= \dfrac{PO'}{PO}= \dfrac{PA}{PO}= \dfrac{4}{8}= \dfrac{1}{2}\)

   Suy ra OB = 2.O'A hay R = 2r

   Ta có: PO' = OO' = R + r = 3 r

   Áp dụng định lí Pitago vào tam giác vuông AOP ta có:

   \(O'P^2 = O'A^2 + PA^2 \ Hay \ ( 3r)^2 = r^2 + 4^2 \Rightarrow r^2 = 2.\)

    Diện tích hình tròn (O) là: \(S = \pi r^2 = 2\pi ( cm^2)\)