Giải bài 7 trang 134 - Sách giáo khoa Toán 9 tập 2

Đề bài

    Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE =\( 60^o\).

Hướng dẫn giải

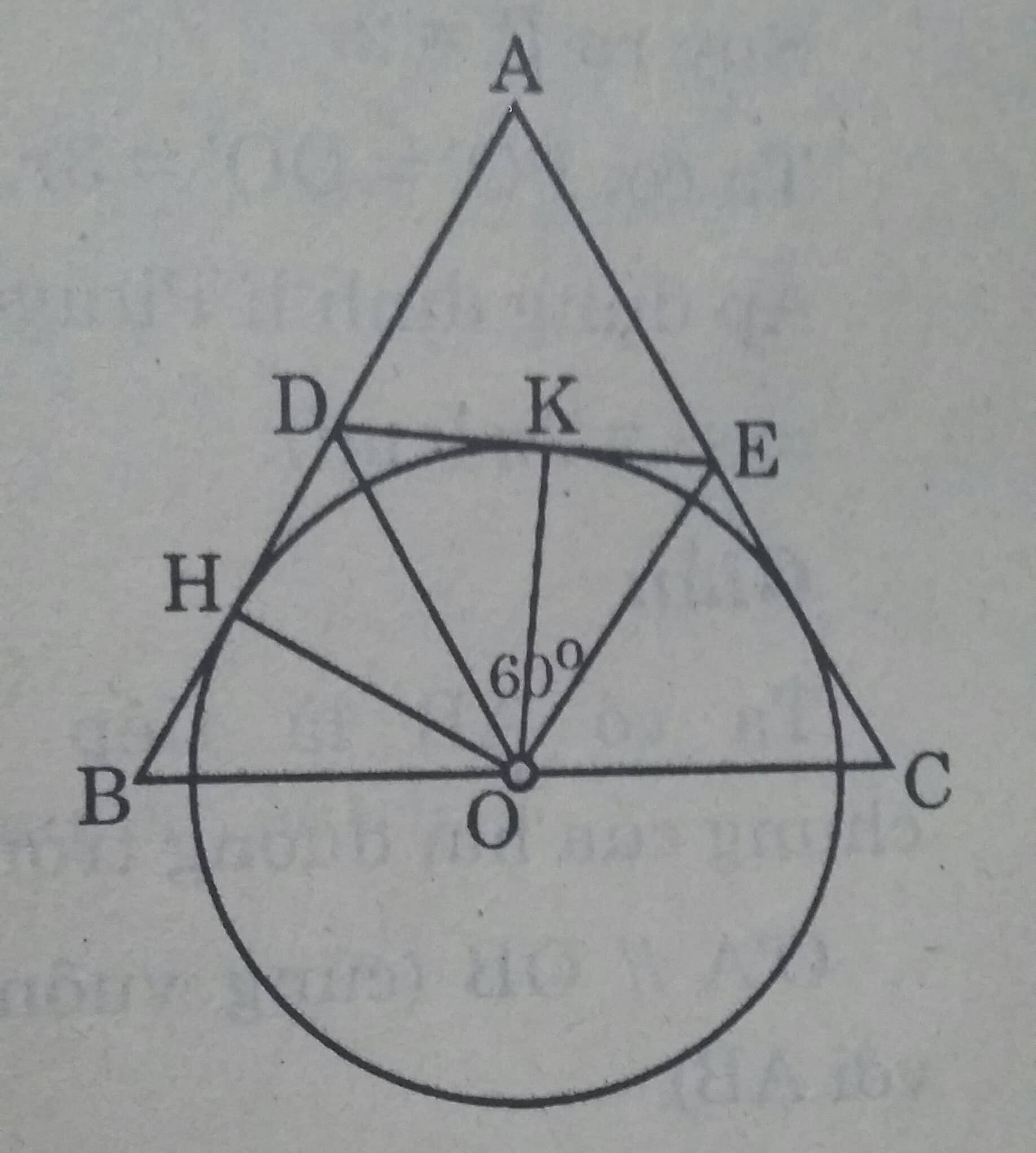
  Xét  \(\Delta BOD \ và \ \Delta CEO \) có:

 \( \widehat{B}= \widehat{C}(= 60^0)\\\widehat{BOD}= \widehat{CEO}( \ vì \ cùng \ cộng \ với \ góc \ \widehat{COE} \ có \ tổng \ bằng \ 120^0)\)   \( \Rightarrow \Delta BOD \approx \Delta CEO (g.g)\\\Rightarrow \dfrac{BD}{OC}= \dfrac{OB}{CE}\\\Rightarrow BD.CE= OB.OC = \dfrac{BC^2}{4}( không \ đổi) \)

   b) Vì

    \( \Delta BOD \approx \Delta CEO \ nên \\ \dfrac{BD}{OC}= \dfrac{OD}{CE} \Rightarrow \dfrac{BD}{OB}= \dfrac{OD}{OE} \\\ Mặt \ khác \ \widehat{B}=\widehat{DOE}= 60^0\\ Do \ đó \ \Delta BOD \approx \Delta OED (g.g) Suy \ ra \ \widehat{BOD}= \widehat{ODE}\)

   Vậy tia DO là tia phân giác của góc BDE.

   c) Gọi H là tiếp điểm của đường tròn (O) với cạnh AB.

   Ta có \(OH \perp AB.\)

  Vẽ \(OK \perp DE.\) thì OK = OH ( tính chất của điểm nằm trên tia phân giác).

   Do đó đường tròn (O) tiếp xúc với DE.