Giải bài 15 trang 135 - Sách giáo khoa Toán 9 tập 2

Đề bài

   Tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (O).Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB ở D và E. Chứng minh:

   a) \(BD^2\) = AD.CD

   b) Tứ giác BCDE là tứ giác nội tiếp

   c) BC song song với DE

Hướng dẫn giải

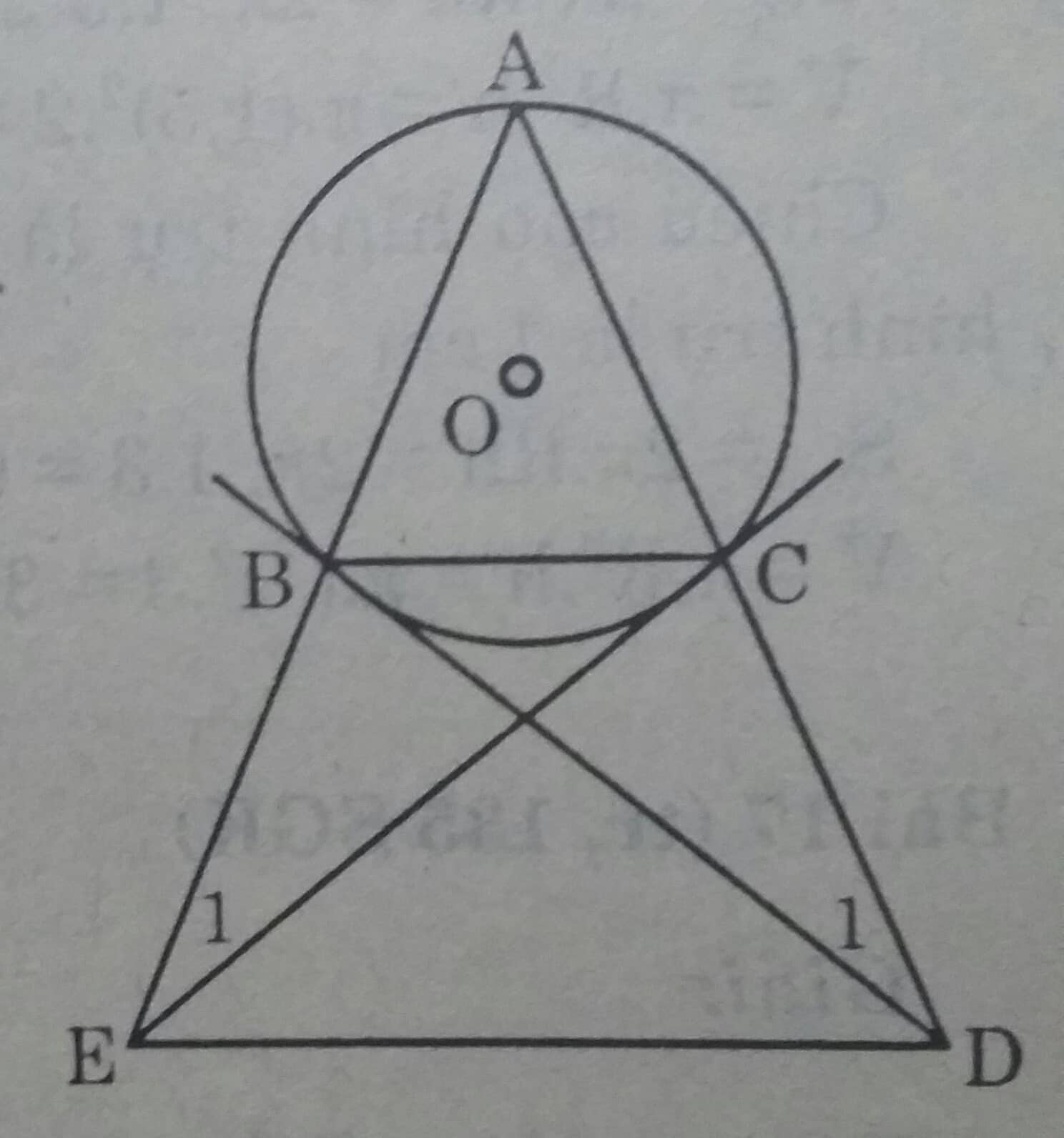
 a) Xét  \(\Delta ABD \ và \ \Delta BCD \ có:\\ \)

    \( \widehat{A}= \widehat{CBD}\) ( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung)

   \(\widehat{D_1} \ chung \ \Rightarrow \Delta ABD \approx \Delta BCD (g.g)\\ \Rightarrow \dfrac{BD}{CD}= \dfrac{AD}{BD} \Rightarrow BD^2 = AD.CD.\)

   b) Các góc \(\widehat{ D_1} \ và \ \widehat{E_1}\) là góc có đỉnh ở bên ngoài đường tròn nên

   \(\widehat{D_1}= \dfrac{\stackrel\frown{AB}-\stackrel\frown{BC}}{2} ; \widehat{E_1}= \dfrac{\stackrel\frown{AC}-\stackrel\frown{BC}}{2} \)

   Mặt khác

    \(\stackrel\frown{AB}= \stackrel\frown{AC} ( Vì \ AB = AC) \\ Nên \ \widehat{D_1}= \widehat{E_1} \Rightarrow\)

   Tứ giác BCDE là tứ giác nội tiếp.

   c) Ta có 

   \( \widehat{BED}= \widehat{ACB} ( \ cùng \ bù \ với \ góc \ \widehat{BCD}).\\ Mặt \ khác \ \widehat{ABC}= \widehat{ACB}( hai \ góc \ đáy \ của \ tam \ giác \ cân)\\ Suy \ ra \ \widehat{ABC} = \widehat{BED}.\)

   Do đó BC // DE.