Giải bài 14 trang 135 - Sách giáo khoa Toán 9 tập 2

Đề bài

   Dựng tam giác ABC, biết BC = 4cm, góc A = 60o, bán kính đường tròn nội tiếp tam giác bằng 1cm.

Hướng dẫn giải

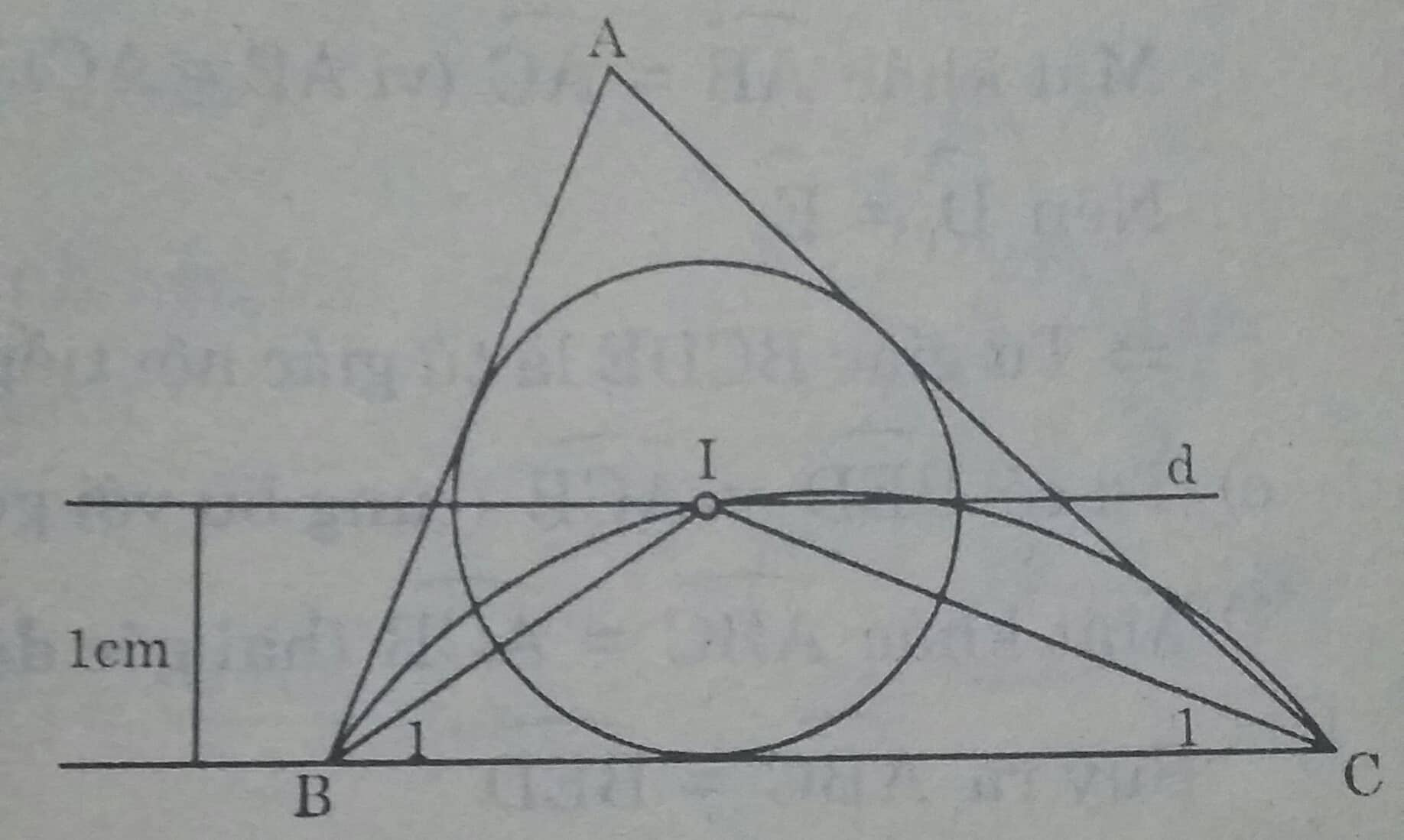
   Phân tích:

   Giải sử dựng được tam giác ABC thỏa mãn đề bài.

   Tâm $I$ của đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác nên:

   $\widehat{BIC}= 180^0 - (\widehat{B_1}+ \widehat{C_1}) = 180^0 - \dfrac{\widehat{B }+ \widehat{C }}{2}= 120^0$

  Vậy điểm $I$ phải thỏa mãn hai điều kiện:

   -  $I$ nằm trên cung chứa góc $120^0$ dựng trên đoạn BC.

   - $I$ nằm trên đường thẳng d // BC và cách BC là 1 cm.

   Cách dựng:

   Dựng đoạn BC = 4cm.

   Dựng cung chứa góc $120^0$ dựng trên đoạn BC.

   Dựng đường thẳng d // BC và cách BC là 1 cm, cắt cung chứa góc nói trên tại điểm $I$ .

   Dựng đường tròn ( $I$ ; 1cm)

   Từ B và C dựng các tiếp tuyến với đường tròn này, chúng cắt nhau tại A.

   $\Delta ABC$ là tam giác phải dựng.

   Chứng minh:

   Ta phải chứng minh $\widehat{A}= 60^0$

   Theo cách dựng ta có $\widehat{BIC}= 120^0$

   $​​\Rightarrow \widehat{B_1}+ \widehat{C_1}= 60^0( \ tổng \ các \ góc \ trong \ tam \ giác \ bằng \ 180^0 )\\​​\Rightarrow \widehat{B }+ \widehat{C }= 120^0 ( \ tính \ chất \ của \ tia \ phân \ giác \ IB, IC)\\ \Rightarrow \widehat{A }= 60^0 ( \ tổng \ các \ góc \ trong \ tam \ giác \ bằng \ 180^0)$

   Biện luận :  Do tính đối xứng của hình nên bài toán có một nghiệm hình.