150 câu trắc nghiệm Nguyên hàm - Tích phân nâng ca...

Câu 1 : Giá trị m để hàm số $F (x) = m x^{3} + (3 m + 2) x^{2} - 4 x + 3$ là một nguyên hàm của hàm số $f (x) = 3 x^{2} + 10 x - 4$

A. m = 1.
B. m = 0.
C. m = 2.
D. m = 3.

Câu 2 : Biết hàm số $f (x) = {(6 x + 1)}^{2}$ có một nguyên hàm là $F (x) = a x^{3} + b x^{2} + c x + d$ thoả mãn điều kiện F(-1) = 20. Tính tổng a + b + c + d.

A. 46.
B. 44.
C. 36.
D. 54.
Câu 3 : Tìm nguyên hàm: $K = \int \frac{\ln x \sqrt[3]{2 + \ln^{2} x}}{x} d x .$

A. $\frac{3}{8} \sqrt[3]{{(\ln^{2} x + 2)}^{4}} + C$
Câu 4 : Tìm nguyên hàm của $I = \int \frac{d x}{2 \sin^{2} x - 3 \sin 2 x + 2}$ .

A. $\frac{1}{2} \ln |\frac{t - 1}{2 \tan x - 1}| + C$
B. $\frac{1}{2} \ln |\tan x| + C$
C. $\frac{1}{2} \ln |\tan 2 x| + C$
D. Đáp án khác
Câu 5 : Tìm nguyên hàm của: $J = \int \frac{d x}{2 \cos x - \sin x + 1}$

A. $\frac{1}{2} \ln |\tan \frac{x}{2}| - x + C$
B. $\frac{1}{2} \ln |\tan \frac{x}{2} + 4| - \ln x + C$
C. $\frac{1}{2} \ln |\tan \frac{x}{2} + 3| - 2 x + C$
D. Đáp án khác

Câu 6 : Tìm nguyên hàm: $I = \int \frac{\sin^{4} 2 x . c o s^{3} x}{\tan (x + \frac{π}{4}) \tan (x - \frac{π}{4})} d x$ .

A. $16 (\frac{\sin^{11} x}{11} - \frac{\sin^{9} x}{3} + \frac{3 \sin^{7} x}{7} - \frac{\sin^{5} x}{5} + C)$
B. $16 (\frac{\sin^{11} x}{11} + \frac{\sin^{9} x}{3} + \frac{\sin^{7} x}{7} - \frac{\sin^{5} x}{5} + C)$
C. $16 (\frac{\sin^{11} x}{11} - \frac{\sin^{9} x}{3} + \frac{\sin^{7} x}{7} + \frac{\sin^{5} x}{5} + C)$
D. Tất cả đều sai
Câu 7 : Tìm nguyên hàm: $I = \int \frac{e^{x} d x}{e^{x} + 4 e^{- x}}$ .

A. $\frac{1}{2} x + \frac{1}{2} \ln |e^{x} + 4 e^{- x}| + C$
B. $\frac{1}{2} x + \ln e^{x} + 4 e + C$
C. $\frac{1}{2} + \frac{1}{3} \ln e^{x} + 4 e^{- x} + C$
D. Đáp án khác
Câu 8 : Tìm nguyên hàm $J = \int \frac{(\ln x + 1) \ln x}{{(\ln x + 1 + x)}^{3}} d x$ .

A. $\frac{x^{2}}{2 \ln x - 1 + x} - \frac{x}{2 (\ln x + x)} + C$
B. $\frac{x^{2}}{2 \ln x - 1 - x} - \frac{x}{2 (\ln x + 2 x)} + C$
C. $\frac{x^{2}}{2 \ln x - 1 + x} + 2 \frac{x}{2 (\ln x + x)} + C$
D. Đáp án khác
Câu 9 : Hàm số $f (x) = x \sqrt{x + 1}$ có một nguyên hàm là F(x). Nếu F(0) = 2 thì F(3) bằng

A. $\frac{146}{15}$
B. $\frac{116}{15}$
C. $\frac{886}{105}$
D. $\frac{105}{886}$

Câu 10 : Gọi F(x) là một nguyên hàm của hàm số f(x) = xcosx thỏa mãn F(0) = 1. Khi đó phát biểu nào sau đây đúng?

A. F(x) là hàm số chẵn.
B. F(x) là hàm số lẻ.
C. Hàm số F(x) tuần hoàn với chu kì là .
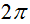D. Hàm số F(x) không là hàm số chẵn cũng không là hàm số lẻ.
Câu 11 : Một nguyên hàm F(x) của hàm số $f (x) = \frac{\sin 2 x}{\sin^{2} x + 3}$ thỏa mãn F(0) = 0 là

A. $\ln |1 + \frac{\sin^{2} x}{3}|$
B. $\ln |1 + s i n^{2} x|$
C. $\frac{\ln |2 + \sin^{2} x|}{3}$
D. $\ln |\cos^{2} x|$
Câu 12 : Tìm nguyên hàm: $I = \int \sin x . \ln (\cos x) d x$

A. –cosxln(cosx)-cosx+C
B. cosx. lnsinx +sinx +C
C.-sinx.ln(cosx)-cosx+C
D. sinx.ln(sinx)-sinx+C
Câu 13 : Tìm nguyên hàm: $J = \int x \ln \frac{x - 1}{x + 1} d x$

A. $\frac{1}{2} x^{2} \ln \frac{x - 1}{x + 1} - 2 \ln |x + 1| + 2 \frac{1}{x + 1} + C$
B. $\frac{1}{2} x^{2} \ln \frac{x - 1}{x + 1} + 12 \ln |x + 1| - \frac{1}{x + 1} + C$
D. Đáp án khác

Câu 14 : Cho $f (x) = \frac{4 m}{π} + \sin^{2} x$ .Tìm m để nguyên hàm của hàm số f(x) thỏa mãn F(0)=1 và $F (\frac{π}{4}) = \frac{π}{8}$

A. -3/4
B. 3/4
C. -4/3
D. 4/3
Câu 15 : Tìm nguyên hàm của hàm số $f (x) = \frac{2 \sin^{3} x}{1 + \cos x} .$

A. $\int f (x) d x = \cos^{2} x - 2 \cos x + C$
B. $\int f (x) d x = \frac{1}{2} \cos^{2} x - 2 \cos x + C$
C. $\int f (x) d x = \cos^{2} x + \cos x + C$
D. $\int f (x) d x = \frac{1}{2} \cos^{2} x + 2 \cos x + C$
Câu 16 : Tìm nguyên hàm của hàm số $f (x) = \frac{\cos^{3} x}{\sin^{5} x} .$

A. $\int f (x) d x = \frac{c o t^{4} x}{4} + C$
B. $\int f (x) d x = \frac{- c o t^{4} x}{4} + C$
C. $\int f (x) d x = \frac{c o t^{2} x}{2} + C$
D. $\int f (x) d x = \frac{\tan^{4} x}{4} + C$
Câu 17 : Tìm nguyên hàm: $I = \int \frac{\sin^{4} x}{\cos^{2} x} d x$

A. tanx - 2x + sin2x + C
B. tanx - 1,5x + 0,25 sin2x + C
C. cot2x - 0,5 x - cos2x + C
D. Đáp án khác

Câu 18 : Tìm nguyên hàm: $I = \int \cos^{4} 2 x d x$

A. 3x + sin4x + sin8x + C
B. 2x - cos2x - sin4x + C
C. $\frac{3 x}{8}$ + sin4x + sin8x + C
D. Đáp án khác
Câu 19 : Tìm nguyên hàm: $J = \int (\cos 3 x . \cos 4 x + \sin^{3} 2 x) d x$

A. $\frac{1}{14} \sin 7 x - \frac{1}{2} \sin x - \frac{3}{8} \cos 2 x + \frac{1}{24} \cos 6 x + C$
B. $\frac{1}{14} \sin 7 x + \frac{1}{2} \sin x + \frac{3}{8} \cos 2 x + \frac{1}{24} \cos 6 x + C$
C. $\frac{1}{14} \sin 7 x + \frac{1}{2} \sin x - \frac{3}{8} \cos 2 x + \frac{1}{24} \cos 6 x + C$
D. $\frac{1}{14} \sin 7 x + \frac{1}{2} \sin x - \frac{3}{8} \cos 2 x - 2 \frac{1}{24} \cos 6 x + C$
Câu 20 : Tìm nguyên hàm: $I = \int (\frac{1}{\ln^{2} x} - \frac{1}{\ln x}) d x$

A. $\frac{x}{\ln x} + C$
B. $\frac{x}{\ln x} + x + C$
C. x.lnx + C
D. Đáp án khác
Câu 21 : Hàm số F(x) = ln|sin x – cos x| là một nguyên hàm của hàm số

A. $f (x) = \frac{\sin x + \cos x}{\sin x - \cos x}$
B. $f (x) = \frac{\sin x - \cos x}{\sin x + \cos x}$
C. $f (x) = \frac{1}{\sin x + \cos x}$
D. $f (x) = \frac{1}{|\sin x - \cos x|}$

Câu 22 : Tính $\int e^{\cos^{2} x} \sin 2 x d x$ bằng:

A. $e^{\sin x} + x + C$
B. $- e^{\cos^{2} x} + C$
C. $e^{- 2 \sin x} + C$
D. $- e^{\sin 2 x} + C$
Câu 23 : Tính $\int e^{\sin^{2} x} \sin 2 x d x$ bằng:

A. $e^{\sin^{2} x} + C$
B. $e^{\sin 2 x} + C$
C. $e^{\cos^{2} x} + C$
D. $e^{2 \sin x} + C$
Câu 24 : Biết hàm số $F (x) = - x \sqrt{1 - 2 x} + 2017$ là một nguyên hàm của hàm số $f (x) = \frac{a x + b}{\sqrt{1 - 2 x}}$ . Khi đó tổng của a và b là

A. 3.
B. 2.
C. 0.
D. 1.
Câu 25 : Biết hàm số $F (x) = (m x + n) \sqrt{2 x - 1}$ là một nguyên hàm của hàm số $f (x) = \frac{1 - x}{\sqrt{2 x - 1}}$ . Khi đó tích của m và n là

A. 2
B. -2
C. $\frac{- 2}{3}$
D. $\frac{- 2}{9}$

Câu 26 : Biết hàm số F(x) là một nguyên hàm của hàm số $f (x) = \frac{\ln x}{x \sqrt{\ln^{2} x + 3}}$ có đồ thị đi qua điểm (e; 2016) . Khi đó hàm số F(1) là

A. $\sqrt{3} + 2014$
B. $\sqrt{3} + 2016$
C. $2 \sqrt{3} + 2014$
D. $2 \sqrt{3} + 2016$
Câu 27 : Một nguyên hàm F(x) của hàm số $f (x) = \frac{x}{\cos^{2} x}$ thỏa mãn $F (π) = 2017$ . Khi đó F(x) là hàm số nào dưới đây?

A. F(x) = xtanx + ln|cosx| + 2017.
B. F(x) = xtanx – ln|cosx| + 2018.
C. F(x) = xtanx + ln|cosx| + 2016.
D. F(x) = xtanx – ln|cosx| + 2017.
Câu 28 : Cho hàm số f(x) liên tục trên khoảng (-2; 3). Gọi F(x) là một nguyên hàm của f(x) trên khoảng (-2; 3). Tính 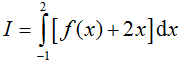, biết F(-1) = 1, F(2) = 4.

A. I = 6.
B. I = 10.
C. I = 3.
D. I = 9.
Câu 29 : Cho $\int_{1}^{3} f (x) d x = - 5, \int_{1}^{3} [f (x) - 2 g (x)] d x = 9 .$ Tính $I = \int_{1}^{3} g (x) d x$

A. I = 14.
B. I = -14.
C. I = 7.
D. I = -7.

Câu 30 : Cho hàm số f(x) liên tục trên đoạn [0; 10] thỏa mãn $\int_{0}^{10} f (x) d x = 7, \int_{2}^{6} f (x) d x = 3$ . Tính $P = \int_{0}^{2} f (x) d x + \int_{6}^{10} f (x) d x$ .

A. P = 10.
B. P = 4.
C. P = 7.
D. P = -4.
Câu 31 : Hàm số $F (x) = (a x^{2} + b x + c) e^{x}$ là một nguyên hàm cùa hàm số $f (x) = x^{2} e^{x}$ thì a + b + c bằng:

A.3.
B.1.
C.3.
D.-2.
Câu 32 : Cho hàm số f(x)= $\tan^{2} x$ có nguyên hàm là F(x). Đồ thị hàm số y = F(x) cắt trục tung tại điểm A(0; 2). Khi đó F(x) là

A. F(x) = tanx – x + 2.
B. F(x) = tanx + 2.
C. $F (x) = \frac{1}{3} \tan^{3} x + 2$
D. F(x) = cotx – x + 2.
Câu 33 : Tính tích phân sau: $I = \int_{0}^{1} \frac{x d x}{\sqrt{3 x + 1} + \sqrt{2 x + 1}}$

A. $\frac{17 - 3 \sqrt{3}}{9}$
B. $\frac{17 - 9 \sqrt{3}}{9}$
C. $\frac{17 - 3 \sqrt{3}}{- 9}$
D. Đáp án khác

Câu 34 : Tính tích phân sau $J = \int_{2}^{7} \frac{x d x}{\sqrt{x + 2} + \sqrt{x - 2}}$

A. $\frac{19 - 5 \sqrt{5}}{9}$
B. $\frac{19 - 5 \sqrt{5}}{3}$
C. $\frac{19 - 5 \sqrt{5}}{6}$
D. 3.
Câu 35 : Tính tích phân sau: $\int_{0}^{2} |x^{2} - 1| d x$

A. 1
B. 2
C. 3
D. 4
Câu 36 : Tính tích phân sau $\int_{- \frac{π}{2}}^{\frac{π}{3}} |\sin x| d x$

A.1
B.1,5
C.2
D.2,5
Câu 37 : Tính tích phân sau $\int_{0}^{π / 2} \sqrt{{(\cos x - \sin x)}^{2}} d x$

A. $2 \sqrt{2}$
B. $2 \sqrt{2} - 2$
C. 3
D. 1

Câu 38 : Tính tích phân $\int_{\frac{π}{4}}^{\frac{3 π}{4}} |\sin 2 x| d x$ ta được kết quả :

A. 3
B. 2
C. 1
D. 0
Câu 39 : Tính tích phân $I = \int_{- 1}^{a} |x^{2} - x| d x$ ta được kết quả I = $\frac{11}{6}$ , khi đó ta có:

A. a = 1.
B. a = 2.
C. a = 3.
D. a = 4.
Câu 40 : Tính tích phân $I = \int_{- 1}^{1} |x^{3} + x^{2} - x - 1| d x$ ta được kết quả I = $\frac{a}{b}$ , khi đó tổng a + b là:

A. 7.
B. 3.
C. 5.
D. 9.
Câu 41 : Tính tích phân $I = \int_{- 2}^{0} |\frac{x^{2} - x - 2}{x - 1}| d x$ ta được kết quả I = a + bln2 + cln3 ( với a, b, c là các số nguyên). Khi đó giá trị của biểu thức $T = 2 a^{3} + 3 b - 4 c$ là:

A. T = -20.
B. T = 3.
C. T = 22.
D. T = 6.

Câu 42 : Tính tích phân $I = \int_{0}^{1} x |x - a| d x, a > 0$ ta được kết quả I=f(a). Khi đó tổng $f (8) + f (\frac{1}{2})$ có giá trị bằng:

A. $\frac{24}{91}$ .
B. $\frac{91}{24}$ .
C. $\frac{17}{2}$ .
D. $\frac{2}{17}$ .
Câu 43 : Tính tích phân $I = \int_{- 1}^{1} |2^{x} - 2^{- x}| d x$ ta được kết quả I = $\frac{a}{\ln b}$ (với a, b là các số nguyên dương). Khi đó $J = \int_{a}^{b} |2 x - 3| d x$ có giá trị bằng:

A. J = $\frac{1}{2} .$
B. J = 2.
C. J = $\frac{1}{3}$ .
D. J = 3.
Câu 44 : Tính tích phân $I = \int_{- 2}^{2} |x + 1| d x$

A. 2
B. 3
C. 4
D. 5
Câu 45 : Biết $I = \int_{1}^{4} \frac{d x}{x^{2} (x + 1)} = a + \ln b$ . Chọn đáp án đúng

A. a – b = 0
B. 2a + b = 4
C. $\frac{1}{2}$ a + b = 1
D. ab = 4

Câu 46 : Tính tích phân $I = \int_{0}^{4} \frac{2 x^{2} + 4 x + 1}{\sqrt{2 x + 1}} d x$

A. $\frac{478}{15}$
B. $\frac{448}{15}$
C. $\frac{408}{15}$
D. $\frac{378}{15}$
Câu 47 : Tính tích phân $I = \int_{0}^{\frac{\sqrt{2}}{2}} \frac{x^{2}}{\sqrt{1 - x^{2}}} d x$

A. $I = \frac{π}{4} - \frac{1}{2}$
B. $I = \frac{π}{8} + \frac{1}{4}$
C. $I = \frac{π}{8} - \frac{1}{4}$
D. $I = \frac{1}{4} - \frac{π}{8}$
Câu 48 : Tính tích phân $I = \int_{0}^{\sqrt{3}} \frac{x^{3}}{\sqrt{x^{2} + 1}} d x$ .

A. $I = \frac{5}{3}$
B. $I = - \frac{5}{3}$
C. $I = \frac{4}{3}$
D. $I = - \frac{4}{3}$
Câu 49 : Tính tích phân: $I = \int_{1}^{3} \frac{3 + \ln x}{{(x + 1)}^{2}} d x$

A. $\frac{3 - \ln 3}{4} + \ln \frac{3}{2}$
B. $\frac{3 - \ln 3}{4} - \ln \frac{3}{2}$
C. $\frac{3 + \ln 3}{4} + \ln \frac{3}{2}$
D. $\frac{3 - \ln 3}{2} + \ln \frac{3}{2}$

Câu 50 : Tính tích phân: $I = \int_{0}^{2} (x - 2) e^{2 x + 1} d x$

A. $\frac{5 e - e^{5}}{6}$
B. $\frac{5 e - e^{5}}{4}$
C. $\frac{5 e + e^{3}}{4}$
D. $\frac{5 e - e^{5}}{2}$
Câu 51 : Tính $I = \int_{1}^{2} \frac{d x}{x {(x + 1)}^{2}}$

A. ln4-2
B. ln3-1
C. ln4-ln3+1
D. Đáp án khác
Câu 52 : Tính tích phân $I = \int_{- 1}^{0} (2 x^{2} + x + 1) \ln (x + 2) d x$

A. $\frac{14}{3} \ln 2 - \frac{17}{191}$
B. $\frac{15}{3} \ln 2 - \frac{17}{191}$
C. $\frac{16}{3} \ln 2 - \frac{119}{36}$
D. $\frac{16}{3} \ln 2 - \frac{17}{191}$
Câu 53 : Cho $I = \int_{0}^{1} x^{2} . \ln (x + 1) d x$ . Mệnh đề nào sau đây là đúng?

A. $- \frac{5}{18} + \frac{2}{3} \ln 2$
B. $- \frac{5}{18} + \frac{3}{2} \ln 2$
C. $\frac{5}{18} + \frac{2}{3} \ln 2$
D. $- \frac{5}{18} - \frac{2}{3} \ln 2$

Câu 54 : Biết $\int_{\frac{π}{4}}^{\frac{π}{2}} \frac{x}{\sin^{2} x} d x = m π + nln 2 (m, n \in ℝ)$ , hãy tính giá trị của biểu thức $P = 2 m + n$

A. P = 1.
B. P = 0,75.
C. P = 0,25.
D. P = 0.
Câu 55 : Tính tích phân $I = \int_{3}^{4} 2 x . \ln (3 x - 6) d x$

A. $I = 12 \ln 6 + 5 \ln 3 - \frac{11}{2}$
B. $I = 12 \ln 6 - 5 \ln 3 + \frac{11}{2}$
C. $I = 12 \ln 6 + 5 \ln 3 + \frac{11}{2}$
D. $I = 12 \ln 6 - 5 \ln 3 - \frac{11}{2}$
Câu 56 : Cho tích phân $I = \int_{\frac{1}{2}}^{3} \frac{d x}{(x + 1) \sqrt{2 x + 3}}$ . Đặt $t = \sqrt{2 x + 3}$ ta được $I = \int_{2}^{3} \frac{m}{t^{2} + n} d t$ (với $m, n \in ℤ$ ). Tính T = 3m + n

A. T = 7.
B. T = 2.
C. T = 4.
D. T = 5.
Câu 57 : Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên đoạn [0; 1] thỏa mãn f(1) = 1 và $I = \int_{0}^{1} f (x) d x = 2$ . Tính tích phân $I = \int_{0}^{1} f' (\sqrt{x}) d x$

A. I = -1.
B. I = 1.
C. I = 2.
D. I = -2.

Câu 58 : Cho hàm số f(x) có đạo hàm trên R và thỏa mãn f(2016) = a, f(2017) = b, $(a; b \in ℝ)$ . Giá trị $I = \int_{2017}^{2016} 2015 f' (x) . f^{2014} (x) d x$ bằng:

A. $I = b^{2017} - a^{2017}$
B. $I = a^{2016} - b^{2016}$
C. $I = a^{2015} - b^{2015}$
D. $I = b^{2015} - a^{2015}$
Câu 59 : Cho hàm số f(x) liên tục trên R và có $\int_{0}^{2} f (x) d x = 3$ .Tính $\int_{- 1}^{1} f (| 2 x |) d x$

A. I = 0.
B. I = $\frac{3}{2}$ .
C. I = 3.
D. I = 6.
Câu 60 : Cho hàm số y = f(x) liên tục trên R và a > 0. Giả sử rằng với mọi $x \in [0; a]$ , ta có f(x) > 0 và f(x)f(a – x) = 1. Tính $I = \int_{0}^{a} \frac{d x}{1 + f (x)}$ .

A. $\frac{a}{2}$ .
B. 2a.
C. $\frac{a}{3}$ .
D. aln(a + 1).
Câu 61 : Nếu $\int_{a}^{x} \frac{f (t)}{t^{2}} d t + 6 = 2 \sqrt{x}$ với x > 0 thì hệ số a bằng:

A. 5.
B. 9.
C. 19.
D. 29.

Câu 62 : Tính tích phân sau : $I = \int_{0}^{\frac{π}{2}} \frac{e^{x} . \sin x}{1 + \sin 2 x} d x$

A. $\frac{1}{2} (e^{\frac{π}{2}} - 1)$
B. $\frac{1}{2} e^{\frac{π}{2}}$
C. $\frac{1}{2} e^{\frac{π}{2}} + 3$
D. Tất cả sai
Câu 63 : Tính tích phân sau : $J = \int_{0}^{2 π} \ln (\sin x + \sqrt{1 + \sin^{2} x}) d x$

A. 0
B. 1
C. 2
D. 3
Câu 64 : Tính tích phân $I = \int_{0}^{\frac{π}{2}} \sin^{2} x \cos x d x$

A. 1
B. $\frac{1}{2}$
C. $\frac{1}{3}$
D.2
Câu 65 : Tính tích phân sau : $I = \int_{0}^{\frac{π}{3}} \ln (1 + \sqrt{3} \tan x) d x$

A. $\frac{πln 2}{3}$
B. $\frac{πln 2}{3} - 2$
C. $\frac{πln 2}{3} + 1$
D. $\frac{πln 2}{3} - 1$

Câu 66 : Giả sử $\int_{0}^{2} \frac{x - 1}{x^{2} + 4 x + 3} d x = a \ln 5 + b \ln 3; a, b \in ℚ$ . Tính P = ab.

A. P = 8.
B. P = -6.
C. P = -4.
D. P = -5.
Câu 67 : Có bao nhiêu số $a \in (0; 20 π)$ sao cho $\int_{0}^{a} \sin^{5} x . \sin 2 x d x = \frac{2}{7}$

A. 9.
B. 10.
C. 19.
D. 20.
Câu 68 : Tìm tất cả các số hữu tỉ m dương thỏa mãn $\int_{0}^{m} \frac{x^{2}}{x + 1} d x = \ln 2 - \frac{1}{2}$

A. m = 3.
B. m = 1.
C. m = 2.
D. m > 3.
Câu 69 : Cho hai số thực a và b thỏa mãn a < b và $\int_{a}^{b} x \sin x d x = π$ đồng thời a cos a = 0 và $b \cos b = - π$ .Tính tích phân $\int_{a}^{b} \cos x d x$ .

A. $I = - π .$
B. $I = π .$
C. $I = \frac{145}{12}$ .
D. I = 0.

Câu 70 : Có bao nhiêu giá trị thực của a thuộc đoạn $[\frac{π}{4}; 2 π]$ thỏa mãn $\int_{0}^{a} \frac{\sin x d x}{\sqrt{1 + 3 \cos x}} = \frac{2}{3}$

A. 2.
B. 1.
C. 4.
D. 3.
Câu 71 : Tính tích phân $I = \int_{- 1}^{2} (|x| - |x - 1|) d x$ ta được kết quả:

A. -2
B. -1
C. 0
D. 1
Câu 72 : Tính tích phân $I = \int_{0}^{2} |3^{x} + x - 4| d x$ ta được kết quả $I = a + \frac{b}{\ln c}$ ( với a, b, c là các số nguyên dương). Khi đó giá trị của biểu thức $T = a^{3} + 3 b^{2} + 2 c$ bằng:

A. 55
B. 36
C. 38
D. 73
Câu 73 : Biết rằng $\int_{0}^{1} 3 e^{\sqrt{1 + 3 x}} d x = \frac{a}{5} e^{2} + \frac{b}{3} e + c (a, b, c, \in ℤ)$ . Tính $T = a + \frac{b}{2} + \frac{c}{3}$ .

A. T = 6.
B. T = 9.
C. T = 10.
D. T = 5.

Câu 74 : Cho hàm số y = f(x) xác định trên $ℝ$ , thỏa mãn $f (x) > 0, \forall x \in ℝ$ và f’(x) + 2f(x) = 0. Tính f(-1), biết rằng f(1) = 1.

A. $e^{- 2}$
B. $e^{3}$
C. $e^{4}$
D. 3
Câu 75 : Biết rằng $\int e^{2 x} \cos 3 x d x = e^{2 x} (a \cos 3 x + b \sin 3 x) + c$
trong đó a, b, c là các hằng số, khi đó tổng a + b có giá trị là

A. $- \frac{1}{13}$
B. $- \frac{5}{13}$
C. $\frac{5}{13}$
D. $\frac{1}{13}$
Câu 76 : Nếu $\int_{1}^{2} f (x) d x = 2$ thì $I = \int_{1}^{2} [3 f (x) - 2] d x$ bằng bao nhiêu?

A. I = 2.
B. I = 3.
C. I = 4.
D. I = 1.
Câu 77 : Tính tích phân sau: $J = \int_{2}^{4} \frac{\sqrt{\ln (9 - x)}}{\sqrt{\ln (x + 3)} + \sqrt{\ln (9 - x)}} d x$

A. 0
B. 1
C. 2
D. 3

Câu 78 : Tính tích phân sau: $K = \int_{0}^{\frac{π}{2}} \ln \frac{{(1 + \sin x)}^{1 + \cos x}}{1 + \cos x} d x$

A. 2ln3-1
B. 3ln2-1
C. 2ln2-1
D. 2ln2
Câu 79 : Diện tích hình phẳng giới hạn bởi các đường $y = x^{3} + 11 x - 6, y = 6 x^{2}$ , x = 0, x = 2. (Đơn vị diện tích)

A. $\frac{4}{3}$
B. $\frac{5}{2}$
C. $\frac{8}{3}$
D. $\frac{18}{23}$
Câu 80 : Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = cosx, y = sinx , đường thẳng $x = \frac{π}{2}; x = \frac{3 π}{2}$ .

A. $\sqrt{3}$
B. $2 \sqrt{2}$
C. $\sqrt{2}$
D. 1.
Câu 81 : Diện tích hình phẳng giới hạn bởi các đồ thị hàm số (H) : $\{\begin{cases} y = x^{3} - 3 x^{2} + 3 x - 1 \\ \begin{matrix} y = 1 - x \\ x = 0, x = 2 \end{matrix} \end{cases}$

A. 1
B. $\frac{3}{2}$
C. 2
D. 3

Câu 82 : Tính diện tích hình phẳng giới hạn bởi :Trục tung, trục hoành và đồ thị hàm số : $y = \frac{2 x + 1}{x + 1}$

A. 1
B. ln2
C. 2
D. 1-ln2
Câu 83 : Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số $y = e^{x}; y = 2$ và đường thẳng x =1

A.e-2
B.2ln2-4
C.e+2ln2
D.e+2ln2-4
Câu 84 : Tính thể tích khối tròn xoay khi quay quanh Ox; giới hạn bởi đồ thị hàm số y = sinx, trục hoành, đường thẳng $x = \frac{π}{2}, x = π$

A. $\frac{π^{2}}{4}$
B. $\frac{π^{2} - 1}{2}$
C. $\frac{π^{2} + 1}{3}$
D. Đáp án khác
Câu 85 : Tính thể tích khối tròn xoay khi quay quanh Ox, giới hạn bởi đồ thị hàm số y = cosx, y = 0, x = 0 , $x = \frac{π}{4}$

A. $\frac{π}{2} (\frac{π}{4} + 2)$
B. $\frac{π}{2} (\frac{π}{4} + \frac{1}{2})$
C. $\frac{π}{2} (\frac{π}{4} + 1)$
D. $\frac{π}{2} (\frac{π}{2} + 2)$

Câu 86 : Tính thể tích khối tròn xoay khi quay quanh Ox, giới hạn bởi đồ thị hàm số $y = x e^{x}$ , y = 0, x = 0, x = 1

A. $\frac{π}{4} (e^{2} - 1)$
B. $\frac{π}{4} (e^{2} + 1)$
C. $\frac{π}{2} (e^{2} - 1)$
D. $\frac{π}{2} (e^{2} + 1)$
Câu 87 : Tính thể tích khối tròn xoay khi quay quanh Ox đồ thị hàm số : $y = \frac{1}{3} x^{3} - x^{2}$ và các đường y = 0, x = 0, x = 3.

A. $\frac{79 π}{35}$
B. $\frac{81 π}{35}$
C. $\frac{79 π}{5}$
D. $\frac{92 π}{35}$
Câu 88 : Hình phẳng (H) được giới hạn bởi đồ thị hai hàm số $y = |x^{2} - 1|, y = |x| + 5$ . Diện tích của (H) bằng

A. $\frac{71}{3}$
B. $\frac{73}{3}$
C. $\frac{70}{3}$
D. $\frac{74}{3}$
Câu 89 : Diện tích hình phẳng giới hạn bởi $(P) : y = x^{2} + 3$ , tiếp tuyến của (P) tại điểm có hoành độ x = 2 và trục tung bằng

A. $\frac{8}{3}$
B. $\frac{4}{3}$
C. 2
D. $\frac{7}{3}$

Câu 90 : Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số $y^{2} - 2 y + x = 0, x + y = 0$ là

A. 9/4
B. 9/2
C. 7/2
D. 11/2
Câu 91 : Diện tích hình phẳng giới hạn bởi các đồ thị hàm số $y = x^{2}; y = \frac{1}{27} x^{2}; y = \frac{27}{x}$ bằng

A. 27ln2
B. 27ln3
C. 28ln3
D. 29ln3
Câu 92 : Diện tích hình phẳng trong hình vẽ sau là

A. $\frac{8}{3}$
B. $\frac{11}{3}$
C. $\frac{7}{3}$
D. $\frac{10}{3}$
Câu 93 : Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = $\sqrt{3}$ , biết thiết diện của vật thể cắt bởi mặt phẳng (P) vuông góc với trục Ox tại điểm có hoành độ x ( $0 \leq x \leq \sqrt{3}$ ) là một hình chữ nhật có độ dài hai cạnh là x và $\sqrt{1 + x^{2}}$

A. 1
B. 2
C. 7/3
D. 3

Câu 94 : Cho parabol (P): y= $x^{2} + m$ . Gọi (d) là tiếp tuyến với (P) qua O có hệ số góc k > 0. Xác định m để thể tích vật thể được sinh ra khi hình phẳng giới hạn bởi (P), (d) và trục Oy quay quanh trục Oy bằng 6 $π$ .

A. m = 4
B. m = 5
C. m = 6
D. m = 7
Câu 95 : Diện tích hình phẳng giới hạn bởi các đường thẳng y = 1, y = x và đồ thị hàm số $y = \frac{x^{2}}{4}$ trong miền $x \geq 0, y \leq 1$ là phân số tối giản $\frac{a}{b}$ . Khi đó b - a bằng

A. 4
B. 2
C. 3
D. 1
Câu 96 : Diện tích hình phẳng giới hạn bởi các đường thẳng $y = \{\begin{cases} - x, n ế u x \leq 1 \\ x - 2, n ế u x > 1 \end{cases}$ và y = $\frac{10}{3} x - x^{2}$ là $\frac{a}{b}$ (với $\frac{a}{b}$ là phân số tối giản) . Khi đó a + 2b bằng

A. 16
B. 15
C. 17
D. 18
Câu 97 : Cho hàm số f(x) liên tục trên R và f(2) = 16, $\int_{0}^{2} f (x) d x = 4$ . Tính I = $\int_{0}^{1} x f' (2 x) d x$

A. 13.
B.12.
C.20.
D.7.

Câu 98 : Cho hàm số f(x) liên tục trên R và các tích phân $\int_{0}^{\frac{π}{4}} f (\tan x) d x$ = 4 và $\int_{0}^{1} \frac{x^{2} f (x)}{x^{2} + 1} d x = 2$ , tính tích phân I = $\int_{0}^{1} f (x) d x$

A. 6
B. 2
C. 3
D. 1
Câu 99 : Tính diện tích hình phẳng giới hạn bởi các đường sau: y = xsin2x, y = 2x, $x = \frac{π}{2}$

A. $\frac{π^{2}}{4} - 4$
B. ${π^{2}}^{} - π$
C. $\frac{π^{2}}{4} - \frac{π}{4}$
D. $\frac{π^{2}}{4} + \frac{π}{4}$
/
Câu 100 : Tính thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi hai đồ thị $y = x^{2} - 4 x + 6$ và y = $- x^{2} - 2 x + 6$

A. 3 $π$
B. $π - 1$
C. $π$
D. 2 $π$
Câu 101 : Biết là $\int_{\frac{2 π}{3}}^{π} \frac{1 - x \tan x}{x^{2} \cos x + x} d x = \ln |\frac{π - a}{π - b}|$ ( a,b $\in ℤ$ ). Tính P = a + b.

A. P = 2
B. P = -4
C. P = 4
D. P = -2

Câu 102 : Cho (H) là hình phẳng giới hạn bởi parabol y = $\sqrt{3} x^{2}$ và nửa đường tròn có phương trình y = $\sqrt{4 - x^{2}}$ với $- 2 \leq x \leq 2$ (phần tô đậm trong hình vẽ). Diện tích của (H) bằng

A. $\frac{2 π + 5 \sqrt{3}}{3}$
B. $\frac{4 π + 5 \sqrt{3}}{3}$
C. $\frac{4 π + \sqrt{3}}{3}$
D. $\frac{2 π + \sqrt{3}}{3}$
Câu 103 : Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên đoạn [1; 4], f(1) = 12 và $\int_{1}^{4} f' (x) d x = 17$ .Giá trị của f(4) bằng

A. 29
B. 5
C. 19
D. 9
Câu 104 : Cho $\int_{0}^{1} \frac{1}{\sqrt{x + 2} + \sqrt{x + 1}} d x = a \sqrt{b} - \frac{8}{3} \sqrt{a} + \frac{2}{3} (a, b \in ℕ^{*})$ .Tính a + 2b

A. a + 2b = 7
B. a + 2b  = 8
C. a + 2b  = -1
D. a + 2b  = 5
Câu 105 : Một đám vi khuẩn tại ngày thứ x có số lượng là N(x). Biết rằng N'(x) = $\frac{2000}{1 + x}$ và lúc đầu số lượng vi khuẩn là 5000 con. Vậy ngày thứ 12 số lượng vi khuẩn (sau khi làm tròn) là bao nhiêu con?

A. 10130.
B. 5130.
C. 5154.
D. 10132.

Câu 106 : Cho $\int_{1}^{2} f (x^{2} + 1) x d x = 2$ . Khi đó I = $\int_{2}^{5} f (x) d x$ bằng

A. 2.
B. 1.
C. -1.
D. 4.
Câu 107 : Biết $\int_{a}^{b} (2 x - 1) d x = 1$ . Khẳng định nào sau đây đúng?

A. b - a = 1
B. $a^{2} - b^{2} = a - b + 1$
C. $b^{2} - a^{2} = b - a + 1$
D. a - b = 1
Câu 108 : Xét hàm số f(x) liên tục trên đoạn [0; 1] và thỏa mãn 2f(x) + 3f(1-x) = $\sqrt{1 - x^{2}}$ .Tính I = $\int_{0}^{1} f (x) d x$

A. $\frac{π}{4}$
B. $\frac{π}{6}$
C. $\frac{π}{20}$
D. $\frac{π}{16}$
Câu 109 : Cho hàm số y = f(x) có $1 \leq f' (x) \leq 4$ với mọi $x \in [2; 5]$ . Hỏi khẳng định nào dưới đây là khẳng định đúng?

A. $3 \leq f (5) - f (2) \leq 12$
B. $- 12 \leq f (5) - f (2) \leq 3$
C. $1 \leq f (5) - f (2) \leq 4$
D. $- 4 \leq f (5) - f (2) \leq - 1$

Câu 110 : Cho m thỏa mãn $\int_{1}^{2} [m^{2} + (4 - 4 m) x + 4 x^{3}] d x = \int_{2}^{4} 2 x d x$ . Nghiệm của phương trình $\log_{3} (x + m) = 1$ là:

A. x = 0.
B. x = 1.
C. x = 2.
D. x = 3.
Câu 111 : Tính tích phân $I = \int_{1}^{5} \frac{1}{x \sqrt{3 x + 1}} d x$ được kết quả I = aln3 + bln5 với a, b là các số hữu tỉ. Giá trị của a² + ab + 3b² là

A. 4.
B. -1.
C. 0.
D. 5.
Câu 112 : Cho $\int_{1}^{2} f (x) d x = - 3$ . Tính $\int_{2}^{4} f (\frac{x}{2}) d x$

A. -6.
B. $\frac{- 3}{2}$ .
C. -1.
D. 5.
Câu 113 : Cho hàm số f(x) thỏa mãn $\int_{0}^{1} (x + 1) f' (x) d x = 10$ và 2f(1) – f(0) = 2. Tính I = $\int_{0}^{1} f (x) d x$

A. I = -12.
B. I = 8.
C. I = 12.
D. I = -8.

Câu 114 : Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và $\int_{0}^{2} F (x) g (x) d x$ = 3 . Tính tích phân hàm: $\int_{0}^{2} G (x) f (x) d x$

A. I = 3.
B. I = 0.
C. I = -2.
D. I = -4.
Câu 115 : Tính S hình phẳng được giới hạn bởi các đường $y = \frac{3^{x} - 1}{(3^{- x} + 1) \sqrt{3^{x} + 1}}$ ; y = 0; x=1

A. $\frac{2 (3 - 2 \sqrt{2})}{\ln 3}$
B. $\frac{2 (2 \sqrt{2} - 1)}{\ln 3}$
C. $\frac{(3 - 2 \sqrt{2})}{\ln 3}$
D. $\frac{(2 \sqrt{2} - 1)}{\ln 3}$
Câu 116 : Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x² , y = 4x - 4 và y = -4x - 4

A) 6/3
B) 16/3
C) 26/3
D) 16/9
Câu 117 : Tính diện tích giới hạn bởi các đường cong y = (x - 1)lnx và y = x - 1.

A. $\frac{e^{2} - 4 e + 5}{4}$
B. $\frac{3 e^{2} - 2 e + 5}{2}$
C. $\frac{7 e^{2} - e + 2}{3}$
D. $\frac{4 e^{2} + 3 e - 2}{5}$

Câu 118 : Tính diện tích giới hạn bởi các đường cong y=(e+1)x; y = (e^x + 1)x

A. $\frac{e}{5} - \frac{19}{100}$
B. $\frac{2 e}{3} - \frac{73}{50}$
C. $\frac{e}{3} - \frac{11}{20}$
D. $\frac{e}{2} - 1$
Câu 119 : Tính diện tích giới hạn bởi các đường cong y = (x - 1)ln(x + 1) và trục hoành

A. 3 – 2ln2
B. $- \frac{3}{4} + 2 \ln 2$
C. $- \frac{5}{4} + 2 \ln 2$
D. 4 + ln2
Câu 120 : Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi y = $\frac{1}{1 + \sqrt{4 - 3 x}}$

A. $\frac{2}{9} (6 \ln \frac{3}{2} - 1)$
B. $\frac{1}{9} (6 \ln \frac{3}{2} - 1)$
C. $\frac{π}{9} (6 \ln \frac{3}{2} - 1)$
D. $\frac{π}{3} (6 \ln \frac{3}{2} + 1)$
Câu 121 : Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi y = $\sqrt{x (3^{x} + 1)}$ trục hoành và x = 1 xung quanh trục hoành.

A. $π (\frac{3}{\ln 3} - \frac{2}{\ln^{2} 3} + \frac{1}{2})$
B. $(\frac{3}{\ln 3} - \frac{2}{\ln^{2} 3} + \frac{1}{2})$
C. $\frac{π}{2} (\frac{5}{\ln 3} - \frac{5}{\ln^{2} 3} + \frac{1}{3})$
D. $\frac{1}{3} (\frac{5}{\ln 3} - \frac{5}{\ln^{2} 3} + \frac{1}{2})$

Câu 122 : Gọi D là miền giới hạn bởi (P): y = 2x - x² và trục hoành. Tính thể tích vật thể V do ta quay (D) xung quanh trục Oy.

A. $\frac{12 π}{13}$
B. $\frac{8 π}{3}$
C. $\frac{2 π}{9}$
D. $\frac{π}{15}$
Câu 123 : Kết quả tính $\int \frac{- x^{3} + 5 x + 2}{4 - x^{2}} d x$ bằng
Câu 124 : Tìm nguyên hàm của hàm số $f (x) = \sin^{3} x . \sin 3 x$ .
Câu 125 : Họ nguyên hàm của hàm số $f (x) = \frac{x^{2} + x + x^{3} + 1}{x^{3}}$ là hàm số nào?

Câu 126 : Gọi F(x) là nguyên hàm của hàm số $f (x) = \sin^{4} (2 x)$ thoả mãn F(0) = 3/8. Khi đó F(x) là:
Câu 127 : Tìm nguyên hàm: $I = \int \frac{d x}{e^{x} + 2 e^{- x} - 3}$
Câu 128 : Tìm nguyên hàm của hàm số $I = \int \frac{\ln x . d x}{x (1 + \sqrt{3 \ln x + 2})}$ với t = $\sqrt{3 \ln x + 2}$
Câu 129 : Tìm nguyên hàm: I= $\int \frac{\ln^{2} x + 1}{x} d x$

Câu 130 : Tìm nguyên hàm: $I = \int \frac{x^{3} - 1}{x (x^{6} + 3 x^{3} + 2)} d x .$
Câu 131 : Tìm nguyên hàm: $J = \int \frac{d x}{x {(x^{6} + 1)}^{2}} .$
Câu 132 : Tìm nguyên hàm của hàm số $f (x) = \frac{1}{\sin x . \cos x}$ .
Câu 133 : Tìm nguyên hàm của hàm số: $f (x) = \cos 2 x (\sin^{4} x + \cos^{4} x) .$

Câu 134 : Tìm nguyên hàm của hàm số $f (x) = (\tan x + e^{2 \sin x}) \cos x .$
Câu 135 : Tìm nguyên hàm: $I = \int \frac{x^{4} d x}{{(x^{2} - 1)}^{2}}$
Câu 136 : Tìm nguyên hàm của hàm số $f (x) = \frac{1}{\sin x + \cos x + \sqrt{2}}$ .
Câu 137 : Tìm nguyên hàm $J = \int \frac{x e^{x} + 1}{{(x + e^{x})}^{2}} d x$

Câu 138 : Kết quả tính $\int 2 x \ln (x - 1) d x$ bằng:
Câu 139 : Tìm nguyên hàm của hàm số $f (x) = \frac{x^{3} - 2 x}{\sqrt{x^{2} + 1}}$
Câu 140 : Tìm nguyên hàm của hàm số: $I = \int \frac{d x}{{(x^{2} - 1)}^{2}}$
Câu 141 : Tìm nguyên hàm của hàm số: $J = \int \frac{x^{3} + 2 x + 1}{x^{2} + 2 x + 1} d x$

Câu 142 : Tính nguyên hàm của hàm số sau: $K = \int \frac{2 x^{2} + 1}{{(x + 1)}^{5}} d x$
Câu 143 : Tính $F (x) = \int \frac{\sin 2 x}{\sqrt{4 \sin^{2} x + 2 \cos^{2} x + 3}} d x$ . Hãy chọn đáp án đúng.
Câu 144 : Một nguyên hàm F(x) của hàm số $f (x) = \ln (x + \sqrt{x^{2} + 1})$ thỏa mãn F(0) = 1. Chọn kết quả đúng
Câu 145 : Tính $F (x) = \int \frac{1 + x \sin x}{\cos^{2} x} d x$ . Chọn kết quả đúng

Câu 146 : Một nguyên hàm F(x) của hàm số $f (x) = \sin x + \frac{1}{\cos^{2} x}$ thỏa mãn điều kiện $F (\frac{π}{4}) = \frac{\sqrt{2}}{2}$ là
Câu 147 : Một nguyên hàm F(x) của hàm số $f (x) = 2 \sin 5 x + \sqrt{x} + \frac{3}{5}$ thỏa mãn đồ thị của hai hàm số F(x) và f(x) cắt nhau tại một điểm nằm trên trục tung là:
Câu 148 : Một nguyên hàm F(x) của hàm số f(x) = a + bcos2x thỏa mãn $F (0) = \frac{π}{2}, F (\frac{π}{2}) = \frac{π}{6}, F (\frac{π}{12}) = \frac{π}{3}$ là
Câu 149 : Cho hàm số $F (x) = a x^{3} + b x^{2} + c x + 1$ là một nguyên hàm của hàm số f(x) thỏa mãn f(1) = 2, f(2) = 3, f(3) = 4. Hàm số F(x) là

Câu 150 : Một nguyên hàm F(x) của hàm số f(x) = tanx.sin2x thỏa mãn điều kiện $F (\frac{π}{4}) = 0$ là

Đáp án có ở chi tiết câu hỏi nhé!!! (click chuột vào câu hỏi).

Lớp 12 Toán học Lớp 12 - Toán học

Xem thêm