Giải bài 13 trang 106 - Sách giáo khoa Toán 9 tập 1

Đề bài

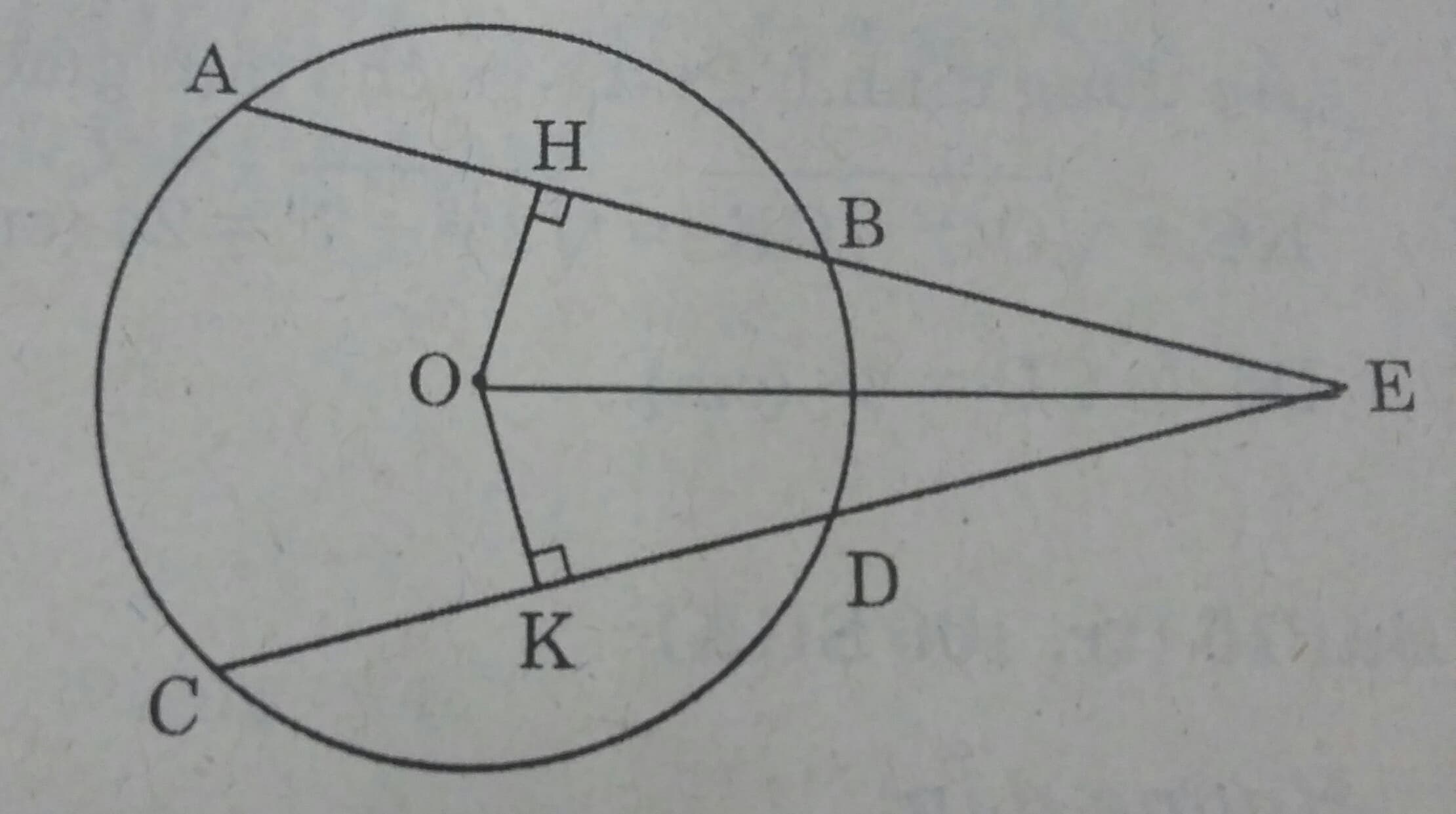
   Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm E nằm bên ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng:

   a) EH = EK

   b) EA = EC.

Hướng dẫn giải

   Hướng dẫn: 

a) Áp dụng định lí: Hai dây bằng nhau thì cách đều tâm.

 Ta có: OH= OK \( \Rightarrow \Delta OEH = \Delta OEK \)  ( cạnh huyền, cạnh góc vuông bằng nhau) \(\Rightarrow EH= EK\) 

b) Chứng minh HA= KC từ đó suy ra EA= EC.

  Giải: 

 a) Có \(OH \perp AB; OK \perp CD\)( vì đường kính đi qua trung điểm của một dây thì vuông góc với dây ấy) 

 Mà AB= CD \(\Rightarrow OH =OK \)( vì hai dây bằng nhau thì cách đều tâm) 

Xét hai tam giác vuông \(\Delta OEH \ và \ \Delta OEK \) có :

 OH =OK, OE là cạnh chung.

 Nên \(\Delta OEH = \Delta OEK \) ( Cạnh huyền và cạnh góc vuông bằng nhau) 

 Vậy EH = EK .

 b) Có \( HA= HB = \frac{AB}{2} \ và \ KC =KD = \frac{CD}{2}\)

 mà AB= CD suy ra: HA= KC 

Vậy EA= Ec ( Vì theo câu a, EH =EK )