Giải bài 43 trang 96 - Sách giáo khoa Toán 9 tập 1

Đề bài

    Đố

   Vào khoảng năm 200 trước Công Nguyên, Ơratôxten, một nhà toán học và thiên văn học Hi Lạp, đã ước lượng được "chu vi" của Trái Đất (chu vi đường Xích Đạo) nhờ hai quan sát sau: 

   1) Một ngày trong năm, ông ta để ý thấy Mặt Trời chiếu thẳng các đáy giếng ở thành phố Xy-en (nay gọi là At-xu-an), tức là tia sáng chiếu thẳng đứng.

    2) Cùng lúc đó ở thành phố A-lếch-xăng-đri-a cách Xy-en 800km, một tháp cao 25m có bóng trên mặt đất dài 3,1m.

   Từ hai quan sát trên, em hãy tính xấp xỉ "chu vi" của Trái Đất.

   

 

Hướng dẫn giải

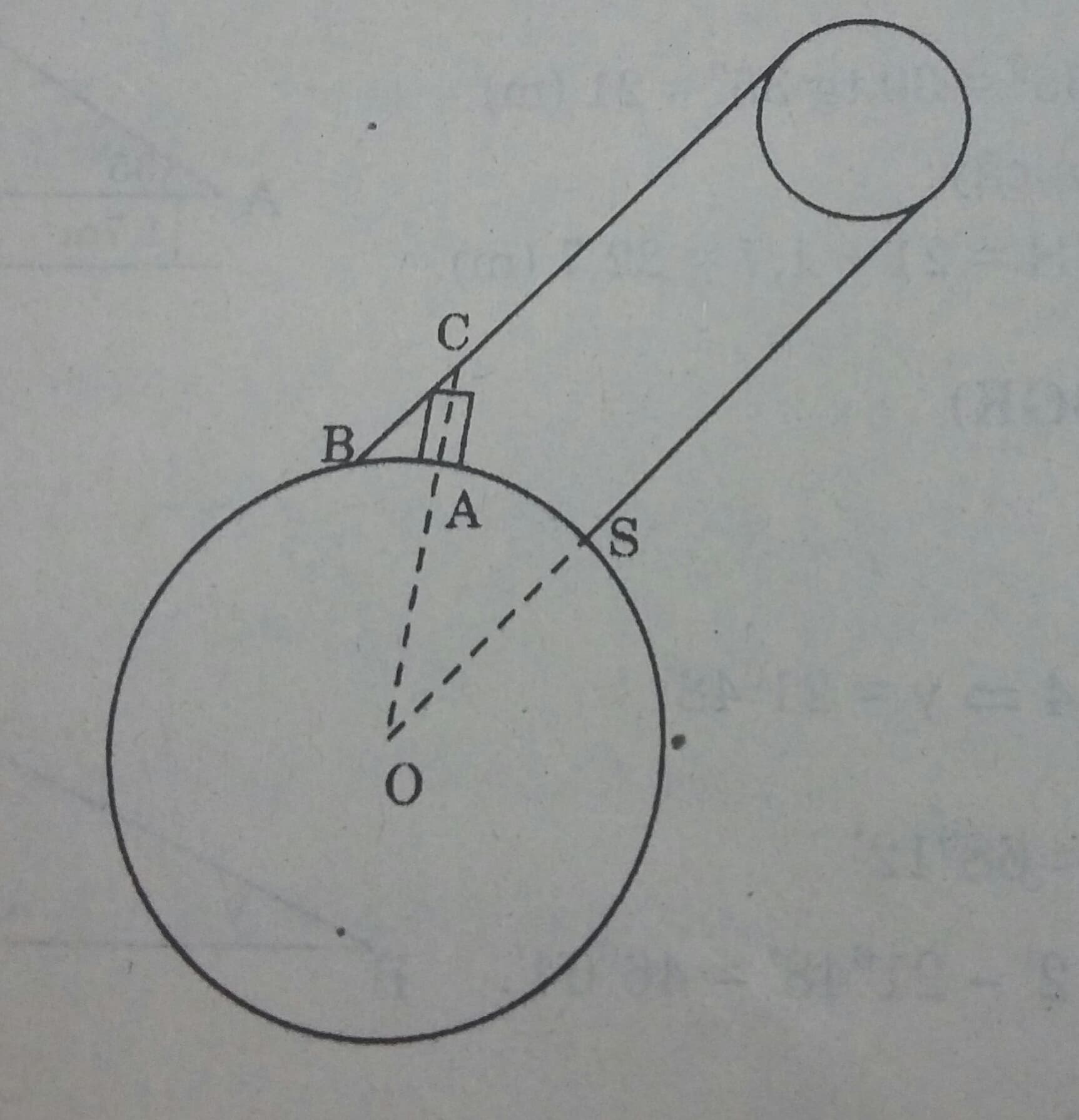
   Xét tam giác vuông ABC có:

   \(tg C= \frac{AB}{AC}= \frac{3,1}{2,5} \approx 1,24 \Rightarrow \widehat{C} \approx 7,0685^0 \)

   \( \Rightarrow \widehat{O}= 7,0686^0 \) ( Vì BC// SO nên \( \widehat{C} \ và\ \widehat{O}\) là hai góc so le) 

   Chu vi trái đất: \(P= \frac{800.360}{7,0686} \approx 40743(km)\)