Bài 64 trang 126 SGK Toán 6 tập 1
Đề bài
Cho hai đoạn thẳng \(AB\) dài \(6cm\). Gọi \(C\) là trung điểm của \(AB\). Lấy \(D\) và \(E\) là hai điểm thuộc đoạn thẳng \(AB\) sao cho \(AD=BE=2cm\). Vì sao \(C\) là trung điểm của \(DE\)?
Hướng dẫn giải
C là trung điểm của đoạn thẳng DE khi C nằm giữa D, E và cách đều D, E (CD = CE).
Lời giải chi tiết
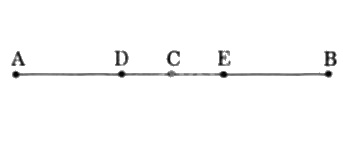
Vì \(C\) là trung điểm của \(AB\) nên \(C\) nằm giữa \(A\) và \(B\) và \(CA=CB= AB : 2 = 6:2 = 3(cm)\).
Trên tia \(AB\) có: \(AD Trên tia \(BA\) có: \(BE Từ các dữ kiện trên suy ra điểm \(C\) nằm giữa \(D\) và \(E\). Mặt khác có \(CD=CE(=1cm)\) nên \(C\) là trung điểm của \(D\) và \(E\).

