Bài 35 trang 87 SGK Toán 6 tập 2
Đề bài
Vẽ góc bẹt xOy. Vẽ tia phân giác Om của góc đó. Vẽ tia phân giác Oa của góc xOm. Vẽ tia phân giác Ob của góc mOy. Tính số đo góc aOb.
Hướng dẫn giải
Góc bẹt là góc có số đo bằng 180 độ.
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.
Lời giải chi tiết
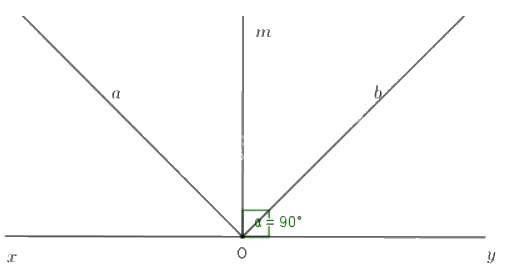
Cách 1. Giải tương tự bài 34 ta được \(\widehat{a'Ob}\) = 900
Ta có: tia Om là tia phân giác của góc xOy nên: \(\widehat {xOm} = \widehat {yOm} = \frac{{\widehat {xOy}}}{2}\) = 900
Lại có: Tia Oa là tia phân giác của góc xOm nên ta có: \(\widehat {xOa} = \widehat {aOm} = \frac{{\widehat {xOm}}}{2}\) \(=\frac{{{{90}^0}}}{2} = {45^0}\)
Tia Ob là tia phân giác của góc yOm nên ta có:\(\widehat {bOm} = \widehat {yOb} = \frac{{\widehat {yOm}}}{2}\) \(=\frac{{{{90}^0}}}{2} = {45^0}\)
Ta có: tia Om nằm giữa hai tia Oa và Ob nên ta có: \(\widehat {aOb} = \widehat {aOm} + \widehat {bOm} = {45^0} + {45^0} = {90^0}\)
Vậy \(\widehat {aOb} = {90^0}\)
Cách 2. Tia Oa là tia phân giác của góc xOm nên góc aOm= \(\frac{\widehat{xOa}}2\)
Tia Ob là tia phân giác của góc yOm nên bOm= \(\frac{\widehat{yOm}}2\).
Tia Om nằm giữa hai tia Oa, Ob do đó: \(\widehat{aOb}\)= \(\widehat{aOm}\) + \(\widehat{bOm}\) = 900

