Giải bài 34 trang 87 - Sách giáo khoa Toán 6 tập 2
Đề bài
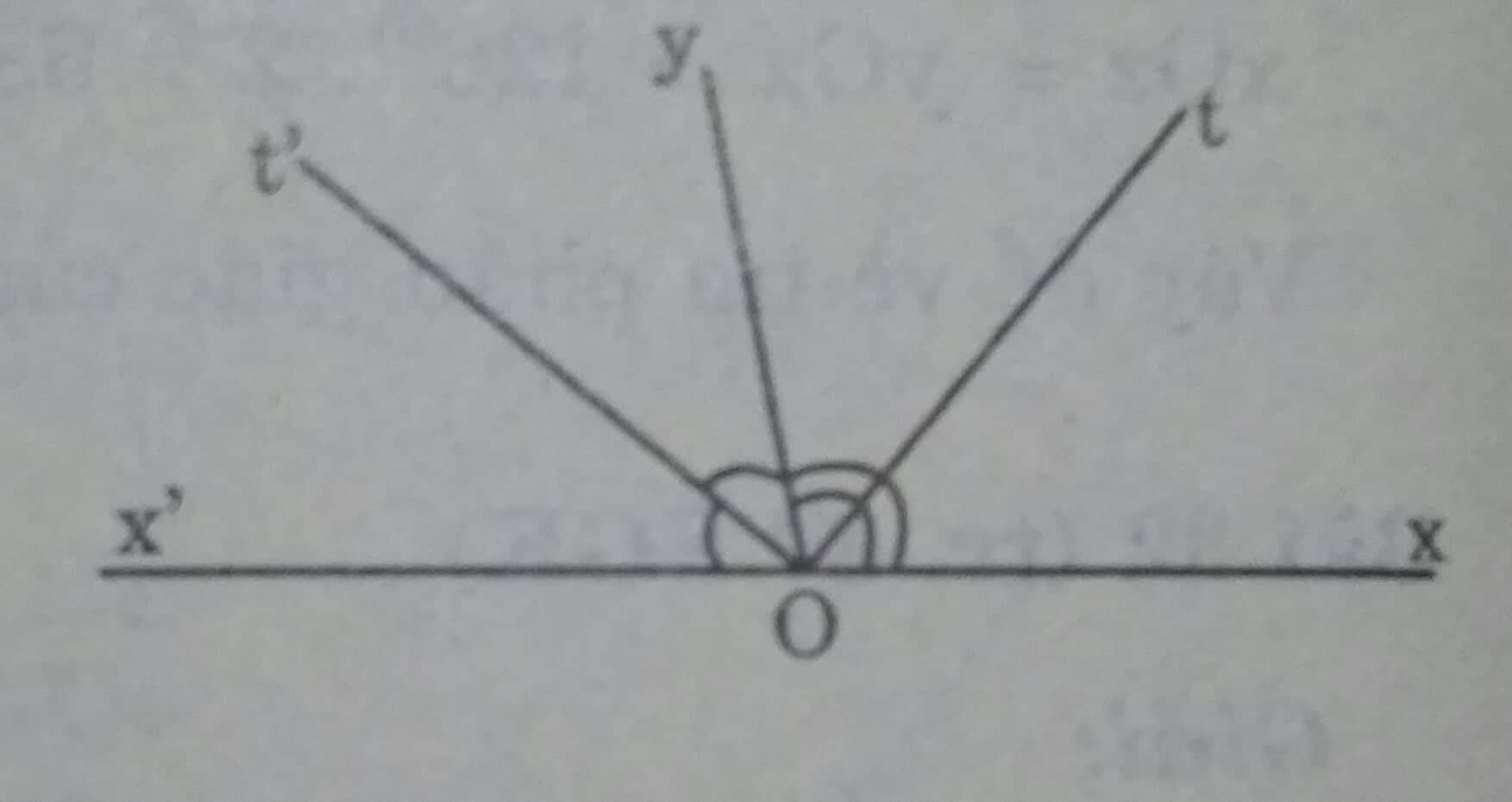
Vẽ hai góc kề bù xOy, yOx', biết góc xOy = 100o. Gọi Ot là tia phân giác của góc xOy, Ot' là tia phân giác của góc x'Oy. Tính góc x'Ot, góc xOt', góc tOt'.
Hướng dẫn giải
Vẽ hai góc kề bù \(\widehat{xOy }\ và \ \widehat{x'Oy}\)
Vẽ hai tia Ox và Ox' đối nhau.
- Vẽ góc \(\widehat{xOy}= 100^0\)
Ta có: \(\widehat{x'Oy}= 180^0 - 100^0 = 80^0\)
Tia Ot là tia phân giác của góc \(\widehat{xOy}\) nên:
\(\widehat{xOt}= \widehat{xOy}: 2= 100^0 : 2= 50^0\)
Hai góc \(\widehat{x'Ot} \ và \ \widehat{xOt}\) kề bù nên:
\(\widehat{x'Ot}= 180^0 - \widehat{xOt}\)
\(\widehat{x'Ot}= 180^0 - 50^0 = 130^0.\)
Tia Ot' là tia phân giác của góc \(\widehat{x'Oy}\) nên.
\(\widehat{x'Ot'}= \widehat{x'Oy}: 2= 80^0 : 2= 40^0\)
Hai góc \( \widehat{x'Ot'} \ và \ \widehat{xOt'}\) kề bù nên:
\(\widehat{xOt'}= 180^0 - \widehat{x'Ot'}\)
\(\widehat{xOt'}= 180^0 - 40^0 = 140^0\)
Tia Ot nằm giữa hai tia Ox và Ot' nên \(\widehat{xOt}+ \widehat{tOt'}= \widehat{xOt'}\)
Do đó \(50^0 + \widehat{tOt'}= 140^0 - 50^0 = 90^0\)