Bài 34 trang 87 SGK Toán 6 tập 2

Đề bài

Vẽ hai góc kề bù xOy  và yOx', biết \(\widehat{xOy}\) =  100⁰ . Gọi Ot là tia phân giác của góc xOy và Ot' là tia phân giác của góc x'Oy. Tính số đo các góc x'Ot, xOt', tOt'.

Hướng dẫn giải

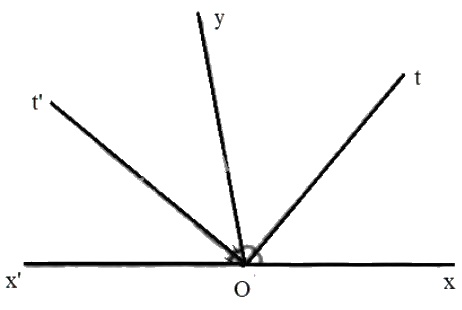
Hai góc xOy và x'Oy là hai góc kề bù mà \(\widehat{xOy}\) =  100⁰ nên \(\widehat{x'Oy}\)=  180⁰ - 100⁰  = 80⁰.

Ot là tia phân giác của góc xOy nên \(\widehat {xOt} = \widehat {tOy} = {{\widehat {xOy}} \over 2} = {{{{100}^0}} \over 2} = {50^0}\)

Ot' là tia phân giác của góc x'Oy nên \(\widehat {x'Ot'} = \widehat {t'Oy} = {{\widehat {x'Oy}} \over 2} = {{{{80}^0}} \over 2} = {40^0}\)

\(\eqalign{
& \widehat {x'Ot} = \widehat {x'Oy} + \widehat {tOy} = {80^0} + {50^0} = {130^0} \cr
& \widehat {xOt'} = \widehat {xOy} + \widehat {t'Oy} = {100^0} + {40^0} = {140^0} \cr
& \widehat {tOt'} = \widehat {tOy} + \widehat {t'Oy} = {50^0} + {40^0} = {90^0} \cr} \)