Giải bài 13 trang 135 - Sách giáo khoa Toán 9 tập 2

Đề bài

   Cho đường tròn (O), cung BC có số đo bằng 120o, điểm A di chuyển trên cung lớn BC. Trên tia đối tia AB lấy điểm D sao cho AD = AC. Hỏi điểm D di chuyển trên đường nào? 

Hướng dẫn giải

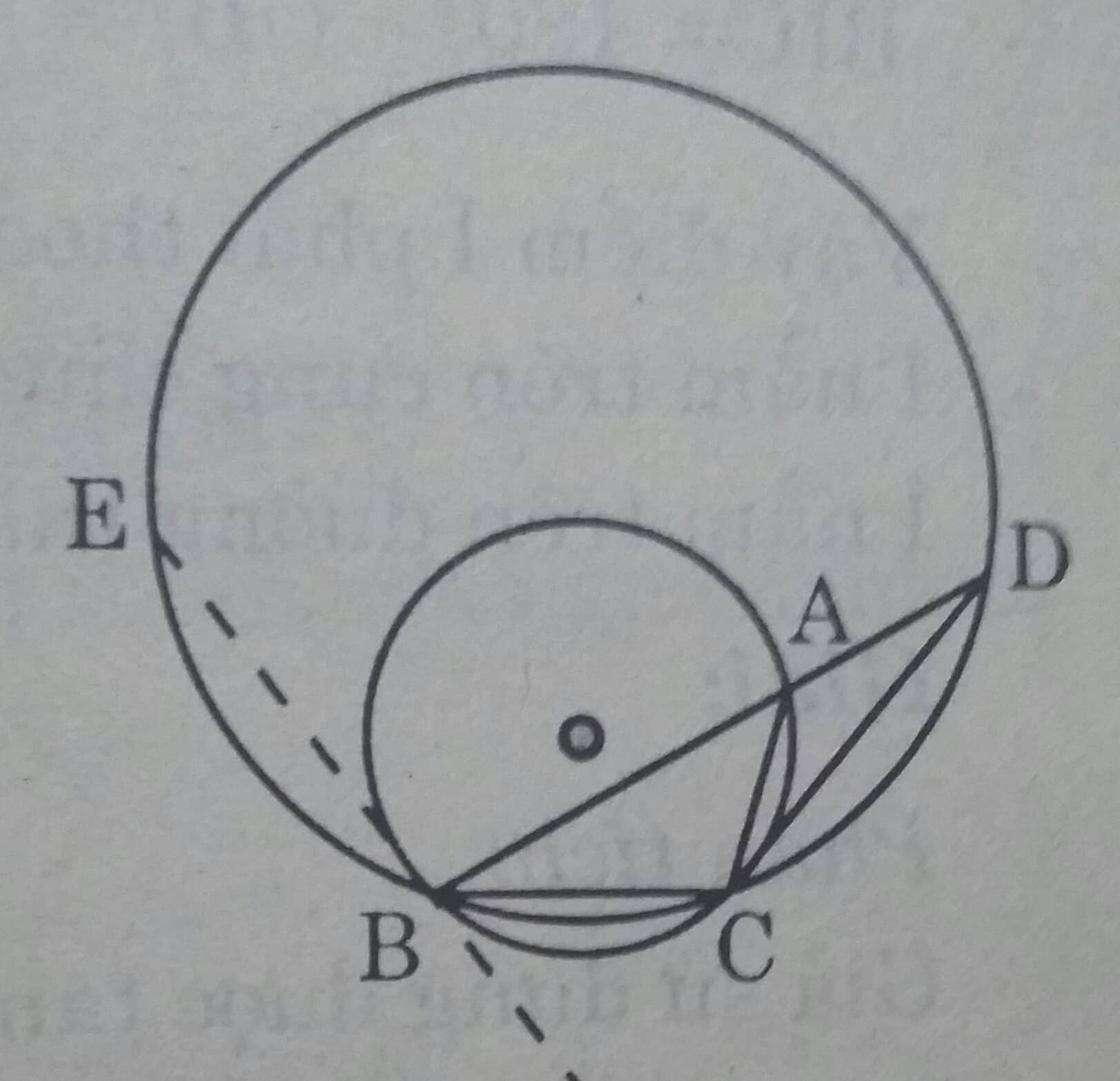
   Góc \(\widehat{BAC}\) nội tiếp nên

   \(\widehat{BAC}= \dfrac{1}{2}sđ \stackrel\frown{BC}= \dfrac{120^0}{2}= 60^0\\\)

   \(\Delta ACD \ có \ AD = AC \ nên \ : \widehat{ADC}=\widehat{ACD}= \dfrac{1}{2}\widehat{BAC}\)

   Vậy \(\widehat{BDC}= 60^0 :2= 30^0\)

   Điểm D nhìn BC cho trước dưới một góc \(30^0\) nên D nằm trên cung chứa góc \(30^0\) dựng trên đoạn BC.

   Khi điểm A trùng với điểm C thì điểm D trùng với điểm C.

   Khi điểm A trùng với B thì điểm D trùng với điểm E ( BE là tiếp tuyến của đường tròn (O) tại điểm B)

   Vậy khi A di chuyển trên cung lớn BC thì điểm D di chuyển trên cung CE thuộc cung chứa góc \(30^0\) dựng trên đoạn BC( cung này cùng phía với A đối với BC)