Bài 37 trang 20 SGK Toán 9 tập 1

Đề bài

Đố: Trên lưới ô vuông, mỗi ô vuông cạnh $1cm$, cho bốn điểm $M,\ N,\ P,\ Q$ (h.3).

Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác $MNPQ$.

Hướng dẫn giải

+ Sử dụng định lí Py-ta-go trong tam giác vuông.

+ Công thức tính diện tích hình vuông cạnh $a$ là: $S=a^2$.

+ Dấu hiệu nhận biết hình vuông: hình thoi có hai đường chéo bằng nhau (hay tứ giác có bốn cạnh bằng nhau và có hai đường chéo bằng nhau) thì là hình vuông.

Lời giải chi tiết

Nối các điểm ta có tứ giác $MNPQ$

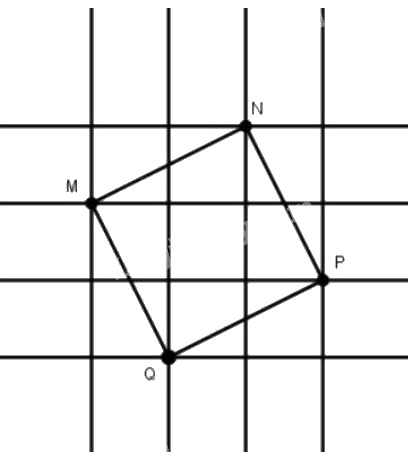
Tứ giác $MNPQ$ có:

- Các cạnh bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài $2cm$, chiều rộng $1cm$. Do đó theo định lí Py-ta-go:

$MN=NP=PQ=QM=\sqrt{2^{2}+1^{2}}=\sqrt{5} (cm)$.

- Các đường chéo bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài $3cm$, chiều rộng $1cm$ nên độ dài đường chéo là:

$MP=NQ=\sqrt{3^{2}+1^{2}}=\sqrt{10}(cm).$

Từ các kết quả trên suy ra $MNPQ$ là hình vuông. Vậy diện tích tứ giác $MNPQ$ bằng $MN^{2}=(\sqrt{5})^{2}=5(cm)$.