Bài 4 trang 69 SGK Toán 9 tập 1

Đề bài

Hãy tính \(x\) và \(y\) trong hình sau:

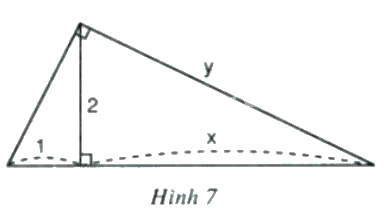
Hướng dẫn giải

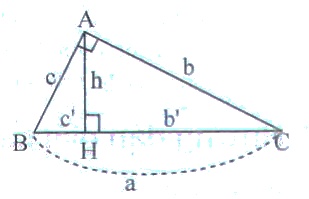
+) Sử dụng hệ thức liên quan đến đường cao và hình chiếu  \(h^2=b'.c'\). Biết \(h,\ c'\) tính được \(b'\).

+) Tính độ dài cạnh huyền: \(a=b'+c'\).

+) Sử dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền \(b^2=b'.a\). Biết \(a,\ b'\) tính được \(b\).

Lời giải chi tiết

Đặt tên các đỉnh của tam giác như hình bên dưới

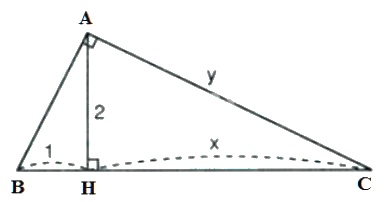
Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\).

Áp dụng hệ thức liên quan đến đường cao, ta có:

                     \(h^{2}=b'.c'\) 

             \(\Leftrightarrow AH^{2}=HB.HC\)

             \(\Leftrightarrow 2^2=1.x\)

             \(\Leftrightarrow 4=x\)

             \(\Leftrightarrow x= 4.\)

Áp dụng hệ thức \(b^{2}=b'.a\), ta có:

                     \(AC^{2}=CH.BC\)

               \(   \Leftrightarrow y^{2}=5. 4\)

              \(\Leftrightarrow y^2=\sqrt{20}\)

              \(\Leftrightarrow y =\sqrt{20}=2\sqrt{5}.\)

Vậy \(x=4,\ y=2\sqrt 5\).