Tóm tắt lý thuyết phương trình mặt phẳng và bài tập trắc nghiệm có lời giải

Tóm tắt lý thuyết phương trình mặt phẳng và bài tập trắc nghiệm có lời giải

Một dạng bài hết sức quan trọng trong chương trình học THPT đó là dạng bài tập về phương trình mặt phẳng trong hệ tọa độ Oxyz. Bài học cung cấp tới bạn đọc các khái niệm về phương trình mặt phẳng và các dạng bài tập tiêu biểu. Chúng tôi hy vọng chúng hữu ích đối vớ bạn!

I. Định nghĩa

1. Phương trình mặt phẳng trong không gian:

Chi tiết tại đây: Phương trình của mặt phẳng

Phương trình mặt phẳng Oxyz có dạng:

\(Ax + By + Cz + D = 0(A^2 + B^2 + C^2 ≠ 0) \)

Phương trình mặt phẳng qua điểm \(M(x_o,y_o,z_o)\) và có vtpt \(\overrightarrow {n}= (A,B,C)\) là:

\(A(x-x_o) + B(y-y_o) + C(z-z_o) = 0\)

Nếu mặt phẳng a cắt các trục Ox,Oy,Oz lần lượt tại \(A(a,0,0), B(0,b,0), C(0,0,c) (a,b,c≠0)\) thì a có phương trình: \(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\)(1)

Ta gọi phương trình (1) là phương trình mặt phẳng theo đoạn chắn.

Trường hợp đặc biệt:

Cho mặt phẳng a : Ax + By + Cz = 0

a qua gốc O suy ra D = 0
a // Ox suy ra A = 0 và D ≠ 0
a qua (chứa) Ox suy ra A = D = 0
a // (Oxy) suy ra A = B = 0 và D ≠ 0
Các trường hợp a //Oy; a //Oz; a qua Oy; a qua Oz; a // (Oxz); a // (Oyz) được suy ra tương tự.

Phương trình các mặt phẳng tọa độ:

(Oxy): z = 0
(Oxz): y = 0
(Oyz): x = 0

Xem ngay tại:

2. Vị trí tương đối giữa hai mặt phẳng

Cho 2 mặt phẳng:

\(a : Ax + By +Cz + D = 0 ( \overrightarrow{ n} = (A,B,C)) \)

\(a' : A'x + B'y +C'z + D' = 0 ( \overrightarrow{ n} = (A',B',C')) \)

a cắt a' \(\leftrightarrow A:B:C \neq A':B':C' \leftrightarrow [\overrightarrow n_\alpha,\overrightarrow n'_\alpha]\neq \overrightarrow {0}\)
a // a' \(\leftrightarrow \dfrac{A}{A'}=\dfrac{B}{B'}=\dfrac{C}{C'}\neq\dfrac{D}{D'}\)
a ≡ a' \(\leftrightarrow \dfrac{A}{A'}=\dfrac{B}{B'}=\dfrac{C}{C'}=\dfrac{D}{D'}\)
a vuông góc a' \(\leftrightarrow [\overrightarrow n_\alpha,\overrightarrow n'_\alpha] =0 \leftrightarrow AA'+BB'+CC'=0\) .

II. Cách viết phương trình mặt phẳng

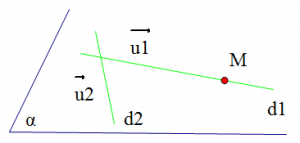
1. Viết phương trình mặt phẳng đi qua 3 điểm

Vì mặt phẳng (P) đi qua 3 điểm A, B, C. Nên mặt phẳng (P) có 1 cặp vector chỉ phương là \(\overrightarrow{AB};\overrightarrow{AC}\)

Khi đó ta gọi \(\overrightarrow{n}\) là một vector pháp tuyến của (P), thì \(\overrightarrow{n}\) sẽ bằng tích có hướng của hai vector \(\overrightarrow{AB}\)và \(\overrightarrow{AC}\). Tức là \(\overrightarrow{n}= [\overrightarrow{AB};\overrightarrow{AC}]\).

phương trình mặt phẳng đi qua 3 điểm

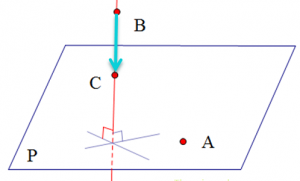
2. Viết phương trình mặt phẳng đi qua 1 điểm và vuông góc với đường thẳng

Vì mặt phẳng (P) đi qua điểm \(M(x_0;y_0;z_0)\)

Mặt phẳng (P) có vector pháp tuyến \(\overrightarrow {n}= (A,B,C)\)

Khi đó phương trình mặt phẳng (P): \(A(x−x_0)+B(y−y_0)+C(z−z_0)=0\)

phương trình mặt phẳng đi qua 1 điểm và vuông góc với đường thẳng

3. Viết phương trình mặt phẳng đi qua 1 điểm và song song với mặt phẳng

Mặt phẳng (P) đi qua điểm \(M(x_0;y_0;z_0)\) và song song với mặt phẳng (Q): Ax + By + Cz + m =0

Vì M thuộc mặt phẳng (P) nên thế tọa độ M và pt (P) ta tìm được M.

Khi đó mặt phẳng (P) sẽ có phương trình là:

\(A(x–x_0)+B(y–y_0)+C(z–z_0)=0\)

Chú ý: Hai mặt phẳng song song có cùng vector pháp tuyến.

III. Một số bài tập trắc nghiệm phương trình mặt phẳng tham khảo

Câu 1: Trong hệ tọa độ Oxyz, a là mặt phẳng đi qua điểm A (2;-1.5) và vuông góc với hai mặt phẳng \(P:3x-2y+z-7=0;Q:5x-4y+3z+1=0\). Phương trình mặt phẳng a là:

A. \(x+2y+z-5=0\)

B. \(2x-4y-2z-10=0\)

C. \(2x+4y+2z-10=0\)

D. \(x+2y-z+5=0\)

Câu 2: Trong hệ tọa độ Oxyz, tọa độ điểm M nằm trên Oy và cách đều hai mặt phẳng: \(P:x+y-z+1=0;Q: x-y+z-5=0\)là:

A. \(M(0;-3;0)\)

B. \(M(0;3;0)\)

C. \(M(0;-2;0)\)

D. \(M(0;1;0)\)

Câu 3: Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (1;2;3). Gọi a là mặt phẳng chức trục Oy và cách M một khoảng lớn nhất. Phương trình của a là:

A. \(x+3z=0\)

B. \(x+2z=0\)

C. \(x-3z=0\)

D. \(x=0\)

Câu 4: Trong hệ tọa độ Oxyz, cho điểm M (1;2;3). Mặt phẳng P qua M và cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích khối tứ diện OABC là nhỏ nhất có phương trình là:

A. \(6x+3y+2z-18=0\)

B. \(6x+3y+2z=0\)

C. \(x+2y+3z-14=0\)

D. \(x+y+z-6=0\)

Ngoài ra để củng cố thêm dạng bài tập này bạn có thể tham khảo thêm tại Phương trình mặt phẳng - Toán lớp 12 Nâng cao

Với những kiến thức chúng tôi đã tổng hợp trên đây, bạn hiểu được bao nhiêu phần trăm bài học, hãy để lại bình luận cho chúng tôi biết. Chúc các bạn có một buổi học vui vả và thu lượm được các kiến thức bổ ích!