Lý thuyết Tỉ số lượng giác của góc nhọn chi tiết nhất

Tỉ số lượng giác của góc nhọn là một trong những bài lý thuyết quan trọng nhất chương trình Toán 9 nghiên cứu về các yếu tố trong một tam giác vuông. Cunghocvui xin gửi tới các bạn bài lý thuyết và một số bài tập toán 9 tỉ số lượng giác của góc nhọn chi tiết nhất. Hy vọng với bài giảng tỉ số lượng giác của góc nhọn, các bạn sẽ thấy hữu ích!

A. Tóm tắt lý thuyết tỉ số lượng giác của góc nhọn

1. Một số kiến thức cần nhớ về tỉ số lượng giác của góc nhọn lớp 9

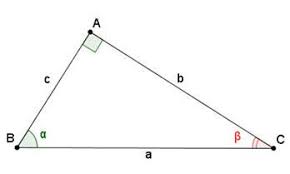
Góc nhọn \(\alpha \) trong một tam giác vuông có các tỉ số lượng giác được xác định theo các công thức như sau:

- Thương của hai độ dài cạnh đối chia cho cạnh huyền thì được gọi là \(sin\alpha \) (\(sin\alpha= \dfrac{AB}{BC}\))

- Thương của hai độ dài cạnh kề chia cho cạnh huyền thì được gọi là \(cos\alpha \) (\(cos\alpha= \dfrac{AC}{BC}\))

- Thương của hai độ dài cạnh đối chia cho cạnh kề thì được gọi là \(tan\alpha \) (\(tan\alpha= \dfrac{AB}{AC}\))

- Thương của hai độ dài cạnh kề chia cho cạnh đối thì được gọi là \(cot\alpha \) (\(cot\alpha= \dfrac{AC}{AB}\))

2. Một số tính chất cần nhớ về tỉ số lượng giác của góc nhọn lớp 9

- Tính chất 1: Nếu tổng của hai góc trong một tam giác bất kì bằng \(90^0\) thì \(sin\alpha= cos\beta\), \(tan\alpha= cot\beta \) và ngược lại \(sin\beta =cos\alpha \) và \(tan\beta =cot\alpha \)

- Tính chất 2: Cho hai góc nhọn \(\alpha \) và \(\beta\), ta có tính chất nếu \(sin\alpha =sin\beta \) hoặc \(cos\alpha =cos\beta \) thì \(\alpha =\beta \)

- Tính chất 3: Có \(\alpha <90^0\), ta có một số tính chất sau:

+ \(tan\alpha >0\), \(cot\alpha >0\), \(sin\alpha \) nằm trong đoạn \(\left [ 0;1 \right ]\), \(cos\alpha \) nằm trong đoạn \(\left [ 0;1 \right ]\)

+ \(sin^2\alpha +cos^2\alpha =1\), \(tan\alpha .cot\alpha =1\)

+ \(1+tan^2\alpha =\dfrac{1}{cos^2\alpha }\), \(1+cot^2\alpha =\dfrac{1}{sin^2\alpha }\)

Tỉ số	\(0^0\)	\(30^0\)	\(45^0\)	\(60^0\)	\(90^0\)
\(sin\alpha \)	\(​​0\)	\(\dfrac{1}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{\sqrt{3}}{2}\)	\(1\)
\(cos\alpha \)	\(1\)	\(\dfrac{\sqrt{3}}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{1}{2}\)	\(​​0\)
\(tan\alpha \)	\(​​0\)	\(\dfrac{\sqrt{3}}{3}\)	\(1\)	\(\sqrt{3}\)
\(cot\alpha \)		\(\sqrt{3}\)	\(1\)	\(\dfrac{1}{\sqrt{3}}\)	\(​​0\)

B. Bài tập về tỉ số lượng giác của góc nhọn

Dạng 1: Tính giá trị của các tỉ số lượng giác, cạnh, góc trong một tam giác

a, Cách làm tỉ số lượng giác của góc nhọn lớp 9

Vận dụng các công thức về tỉ số lượng giác, định lý Py-ta-go, hệ thức lượng đối với tam giác vuông

b, Một số bài tập vận dụng tỉ số lượng giác của góc nhọn luyện tập

Bài 1: Biết rằng \(sin\alpha .cos\alpha =\dfrac{12}{25}\), tính các giá trị của \(sin\alpha \) và \(cos\alpha \)

Hướng dẫn giải bài tập:

Ta có \((sin\alpha +cos\alpha )^2\) = \(sin^\alpha +cos^2\alpha +2.sin\alpha .cos\alpha \) = \(1+2.\dfrac{12}{25}\) = \(\dfrac{49}{25}\)

=> \(sin\alpha +cos\alpha \) = \(\dfrac{7}{5}\) <=> \(sin\alpha \) = \(\dfrac{7}{5}\) - \(cos\alpha \)

Theo dữ kiện đề bài \(cos\alpha \) (\(\dfrac{7}{5}\) - \(cos\alpha \)) = \(\dfrac{12}{25}\) <=> \(\dfrac{7}{5}\)\(cos\alpha \) - \(cos^2\alpha \) - \(\dfrac{12}{25}\) = 0

<=> (5\(cos\alpha \) - 4)(5\(cos\alpha \) - 3) = 0 <=> Hoặc \(cos\alpha \) = \(\dfrac{4}{5}\) hoặc \(cos\alpha \) = \(\dfrac{3}{5}\)

Với  \(cos\alpha \) = \(\dfrac{4}{5}\) thì \(sin\alpha \) = \(\dfrac{3}{5}\)

Với  \(cos\alpha \) = \(\dfrac{3}{5}\) thì \(sin\alpha \) = \(\dfrac{4}{5}\)

Bài 2: Biết rằng \(sin\alpha =\dfrac{3}{15}\), tính các giá trị của \(tan\alpha \), \(cot\alpha \) và \(cos\alpha \)

Với một tác giác vuông ABC có  \(\widehat{A}=90^0\). Ta có công thức tỉ số lượng giác sau:

\(sin\alpha= \dfrac{AC}{BC}\) = \(\dfrac{5}{13}\) => \(\dfrac{AC}{5}=\dfrac{BC}{13}=k\) <=> \(AC=5k\), \(BC=13k\)

Vì \(\Delta ABC \) có \(\widehat{A}=90^0\), vận dụng định lý Py-ta-go ta có:

\(AB^2=BC^2-AC^2=(13k)^2-(5k)^2=144k^2\) => \(AB=12k\)

Theo công thức về tỉ số lượng giác trong tam giác vuông ta có:

\(cos\alpha= \dfrac{AB}{BC}\) = \(\dfrac{12k}{13k}\) = \(\dfrac{12}{13}\)

\(tan\alpha= \dfrac{AC}{AB}\) = \(\dfrac{5k}{12k}\) = \(\dfrac{5}{12}\)

\(cot\alpha= \dfrac{AB}{AC}\) = \(\dfrac{12k}{5k}\) = \(\dfrac{12}{5}\)

Dạng 2: Rút gọn các biểu thức chứa các biểu thức lượng giác và tính giá trị của chúng 

Vận dụng các công thức trong mục "tính chất 3" của phần lý thuyết

a, \(A=(\dfrac{1}{cos2x}+1).tanx\)

b, \(B=\dfrac{sinx+sin3x+sin5x}{cosx+cos3x+cos5x}\)

c, \(C=\dfrac{sin^42x+cos^42x}{tan(\frac{\pi }{4}-x).tan(\frac{\pi }{4}+x)}\)

d, \(D=cos10x+2cos^24x+6cos3x.cosx-cosx-8cosx.cos^33x\)

Hướng dẫn giải làm tỉ số lượng giác của góc nhọn bài tập:

a, \(A=(\dfrac{1}{cos2x}+1).tanx\) 

= \(\dfrac{1+cos2x}{cos2x}.tanx\) = \(\dfrac{2cos^2x}{cos2x}.\dfrac{sinx}{cosx}\) 

= \(\dfrac{2.cosx.sinx}{cos2x}\) = \(\dfrac{sin2x}{cos2x}\) = \(tan2x\)

b, \(B=\dfrac{sinx+sin3x+sin5x}{cosx+cos3x+cos5x}\) 

= \(\dfrac{sinx+sin5x+sin3x}{cosx+cos5x+cos3x}\) 

= \(\dfrac{2sin3x.cos2x+sin3x}{2cos3x.cos2x+cos3x}\) 

= \(\dfrac{sin3x.(2cos2x+1)}{cos3x.(2cos2x+1)}\) = \(\dfrac{sin3x}{cos3x}\) = \(tan3x\)

c, \(C=\dfrac{sin^42x+cos^42x}{tan(\dfrac{\pi }{4}-x).tan(\dfrac{\pi }{4}+x)}\) 

= \(\dfrac{(sin^22x+cos^22x)^2-2.sin^22x.cos^22x}{tan(\dfrac{\pi }{4}-x).cot(\dfrac{\pi }{4}-x)}\) = \(1-\dfrac{sin^24x}{2}\)

d, \(D=cos10x+2cos^24x+6cos3x.cosx-cosx-8cosx.cos^33x\) 

= \(cos10x+1+cos8x-cosx-2(4coss^33x-3cos3x)cosx\) 

= \(2.cos9x.cosx+1-cosx-2.cos9x.cosx\) = \(1-cosx\)

Tham khảo thêm >>> Giải bài tập về Tỉ số lượng giác của góc nhọn Toán 9

Cunghocvui đã mang tới cho các bạn kiến thức lý thuyết và các dạng bài tập về tỉ số lượng giác của góc nhọn chi tiết nhất thông qua bài viết toán 9 tỉ số lượng giác của góc nhọn. Nếu có đóng góp hay thắc mắc gì về bài giảng tỉ số lượng giác của góc nhọn, hãy để lại comment dưới phần bình luận nhé!