Bài 44 trang 86 SGK Toán 9 tập 2

Đề bài

Cho tam giác \(ABC\) vuông ở \(A\), có cạnh \(BC\) cố định. Gọi \(I\) là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm \(I\) khi \(A\) thay đổi.

Hướng dẫn giải

Với đoạn thẳng \(AB\) và góc \(\alpha\, \, (0^0 < \alpha < 90^0)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat{AMB}=\alpha\) là hai cung chứa góc \(\alpha\) dựng trên đoạn \(AB.\)

Lời giải chi tiết

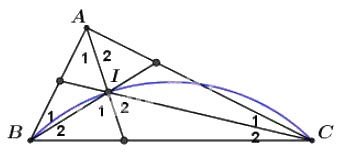
Theo tính chất của góc ngoài tam giác, ta có;

\(\widehat{I_{1}}= \widehat{A_{1}} + \widehat{B_{1}}\)            (1)

\(\widehat{I_{2}} = \widehat{A_{2}}+ \widehat{C_{1}}\)           (2)

 Cộng vế (1) và (2) vế với vế:

\(\widehat{I_{1}}+\widehat{I_{2}} = \widehat{A_{1}}+\widehat{A_{2}}+\widehat{B_{1}}+\widehat{C_{1}}\)

Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0 \Rightarrow \widehat{A_1}+\widehat{B_1}+\widehat{C_1}=90^0\)

Lại có: \(\widehat{A}=90^0 \Rightarrow \widehat{A_1} =  \widehat{A_2} = 45^0.\)

\(\Rightarrow\widehat{BIC} = 90^{\circ} +45^{\circ}= 135^{\circ}.\)

Điểm \(I\) nhìn đoạn thẳng \(BC\) cố định dưới góc \(135^{\circ}\) không đổi, vậy quỹ tích của \(I\) là góc cung chứa góc \(135^{\circ}\) dựng trên đoạn thẳng \(BC\).