Bài 50 trang 87 SGK Toán 9 tập 2

Đề bài

Cho đường tròn đường kính \(AB\) cố định. \(M\) là một điểm chạy trên đường tròn. Trên tia đối của tia \(MA\) lấy điểm \(I\) sao cho \(MI = 2MB.\)

a) Chứng minh \(\widehat{AIB}\) không đổi.

b) Tìm tập hợp các điểm \(I\) nói trên.

Hướng dẫn giải

Với đoạn thẳng \(AB\) và góc \(\alpha\, \, (0^0 <\alpha <90^0)\) cho trước thì quỹ tích các điểm \(m\) thỏa mãn \(\widehat{amb}="\alpha\)" là hai cung chứa góc \(\alpha\) dựng trên đoạn \(ab.\)

Lời giải chi tiết

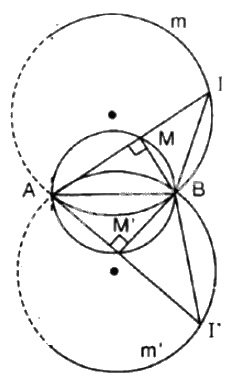
a) Vì \(\widehat{BMA} = 90^0\)  (góc nội tiếp chắn nửa đường tròn) suy ra trong tam giác vuông \(MIB\) có \(tan\widehat{AIB}=\frac{MB}{MI} = \frac{1}{2} \Rightarrow \widehat{AIB}= 26^0 34'.\) 

Vậy \(\widehat{AIB}\) không đổi.

b) Phần thuận:

Khi điểm \(M\) chuyển động trên đường tròn đường kính \(AB\) thì điểm \(I\) cũng chuyển động, nhưng luôn nhìn đoạn thẳng \(AB\) cố định dưới góc \(26^0 34'\) , vậy điểm \(I\) thuộc hai cung chứa góc \(26^0 34'\) dựng trên đoạn thẳng \(AB\) (hai cung \(\overparen{AmB}\) và \(\overparen{Am'B}\))

Phần đảo:

Lấy điểm \(I'\) bất kì thuộc \(\overparen{AmB}\) hoặc \(\overparen{Am'B},\) \(I'A\) cắt đường tròn đường kính \(AB\) tại \(M'.\)

Tam giác vuông \(BMT,\) có \(tan \widehat{I'} = \frac{M'B}{M'I'} = tan 26^0 34’\)

Kết luận: Quỹ tích điểm \(I\) là hai cung \(\overparen{AmB}\) và \(\overparen{Am'B}.\)