Bài 49 trang 87 SGK Toán 9 tập 2

Đề bài

Dựng tam giác \(ABC,\) biết \(BC = 6cm,\)  \(\widehat{A}=40^0\) và đường cao \(AH = 4cm.\)

Hướng dẫn giải

Với đoạn thẳng \(AB\) và góc \(\alpha\, \, (0^0 < \alpha < 90^0)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat{AMB}=\alpha\) là hai cung chứa góc \(\alpha\) dựng trên đoạn \(AB.\)

Lời giải chi tiết

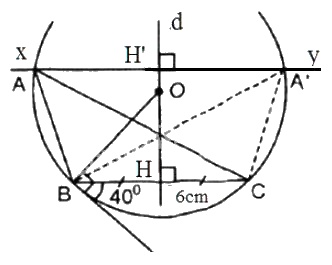
Trình tự dựng gồm 3 bước:

- Dựng đoạn thẳng \(BC = 6cm.\)

- Dựng cung chứa góc \({40^0}\) trên đoạn thẳng \(BC\).

- Dựng đường thẳng \(xy\) song song với \(BC\) và cách \(BC\) một khoảng là \(4cm\) như sau:

Trên đường trung trực \(d\) của đoạn thẳng \(BC\) lấy đoạn \(HH' = 4cm\) (dùng thước có chia khoảng mm). Dựng đường thẳng \(xy\) vuông góc với \(HH'\) tại \(H\).

Gọi giao điểm \(xy\) và cung chứa góc là \(\widehat{A}\), \(\widehat{A'}\). Khi đó tam giác \(ABC\) hoặc \(A'BC\) đều thỏa yêu cầu của bài toán.