Giải bài 44 trang 86 - Sách giáo khoa Toán 9 tập 2

Đề bài

   Cho tam giác ABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm I khi A thay đổi.

Hướng dẫn giải

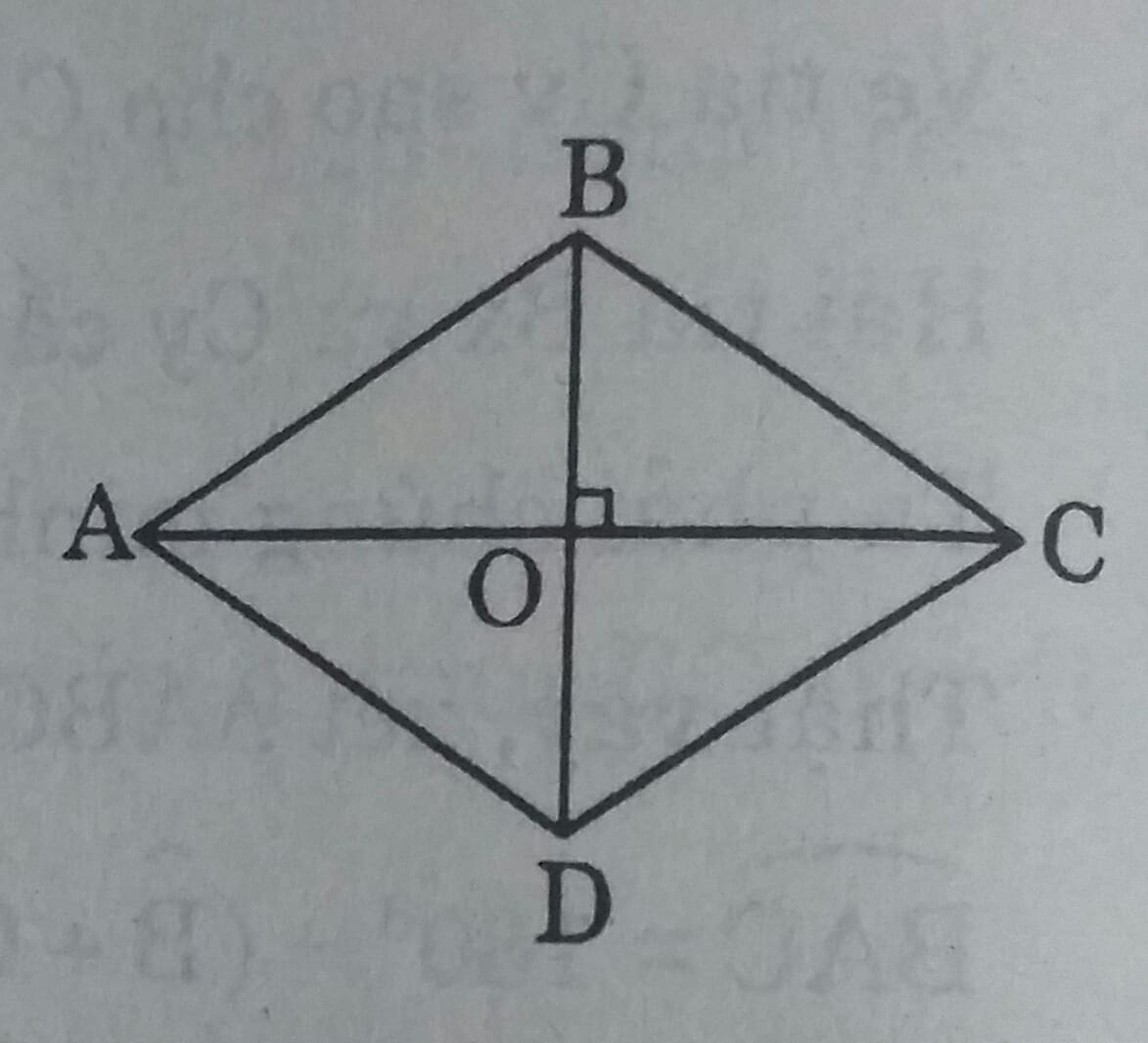
    Phần thuận: Tứ giác ABCD là hình thoi \(\Rightarrow AC \perp BD \Rightarrow \widehat{AOB}=90^0\)

  Vậy điểm O nằm trên đường tròn đường kính AB ( trừ hai điểm A và B)

  Phần đảo: 

  Lấy điểm O bất kì trên đường tròn đường kính AB ( điểm O khác A và B) 

  Vẽ tia AO trên đố lấy điểm C sao cho O là trung điểm của AC.

  Vẽ tia BO trên đó lấy điểm D sao cho O là trung điểm của BD. Ta phải chứng minh tứ giác ABCD là hình thoi.

  Thật vậy, tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường nên tứ giác ABCD là hình bình hành.

  Mặt khác \(\widehat{AOB }= 90^0\)( góc nội tiếp chắn nửa đường tròn đường kính AB) 

  Nên \(AC \perp BD\) 

 Vậy tứ giác ABCD là hình thoi.

 Kết luận: Quỹ tích điểm của O là đường tròn đường kính AB ( trừ hai điểm A và B)