Bài 31 trang 89 SGK Toán 9 tập 1

Đề bài

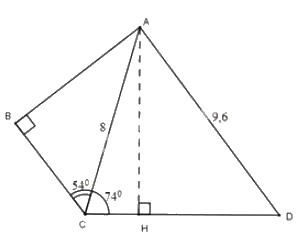
Trong hình 33, $AC=8cm,\ AD=9,6cm,\ \widehat{ABC}=90^o,\ $

$\widehat{ACB}=54^o$ và $\widehat{ACD}=74^o$. Hãy tính:

a) AB;

b) $\widehat {ADC}$.

Hướng dẫn giải

a) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông: $\Delta{ABC}$ vuông tại $B$ thì: $AB=AC. \sin C$.

b) Kẻ thêm đường cao để làm xuất hiện tam giác vuông (Kẻ $AH ⊥ CD$)

+) Sử dụng hệ thức về cạnh và góc trong tam giác vuông: $\Delta{ABC}$ vuông tại $A$ khi đó: $AB=BC. \sin C$ hoặc $AC=AB. \sin B$.

+) Biết $\sin \alpha$ dùng máy tính ta tính được số đo góc $\alpha$.

Lời giải chi tiết

a) Xét tam giác $ABC$ vuông tại $B$ có:

$AB = AC.\sin C = 8.\sin {54^0} \approx 6,472\left( {cm} \right)$

b) Kẻ $AH$ vuông góc với $CD$.

Xét tam giác $ACH$ vuông tại $H$ có:

$AH = AC.\sin C = 8.\sin {74^0} \approx 7,690\left( {cm} \right)$

Xét tam giác $AHD$ vuông tại $H$ có:

$\sin {\rm{D}} = \dfrac{AH}{AD} \approx \dfrac{7,690}{9,6} \approx 0,801 \Rightarrow \widehat D \approx {53^0}$.