Giải bài 31 trang 89 - Sách giáo khoa Toán 9 tập 1
Đề bài
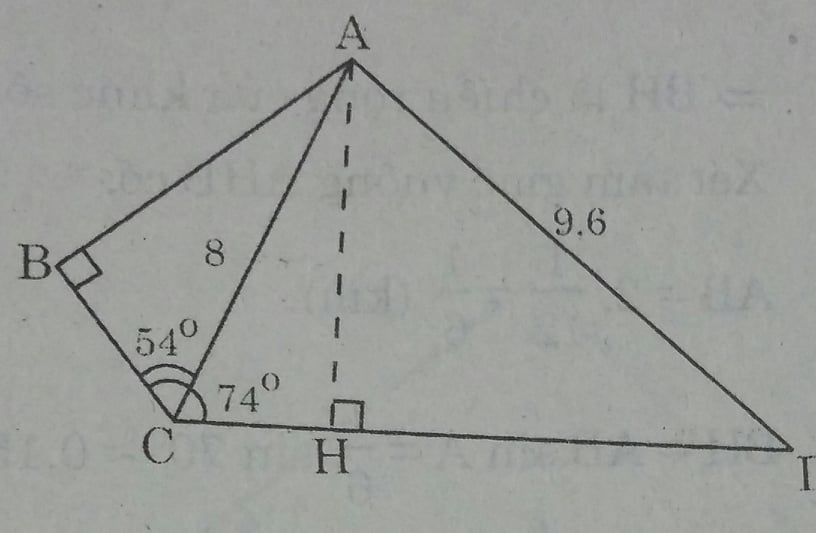
Trong hình 33, AC = 8cm, AD = 9,6 cm, ∠ABC = 90\(^0\), ∠ACB = 54\(^0\) và ∠ACD = 74\(^0\).
Hướng dẫn giải
Hướng dẫn:
Kẻ thêm đường cao AH của tam giác ACD.
Vận dụng hệ thức giữa các cạnh và các góc của một tam giác vuông để tính độ dài AB và \(\widehat{ADC}\)
b=a.sin B=a.cos C
c= a.sin C= a.cos B.
Giải:
a) Xét tam giác vuông ABC có:
\(AB=AC.sin C= 8. sin 54^0 \approx 6,472.\)
b) Kẻ đường cao AH của tam giác ACD ( \(( AH \perp CD ) \)
Xét tam giác vuông AHC có: \(AH= AC.sin C= 8.sin 74^0 \approx 7,690\)
Xét tam giác vuông AHD có: \(sin D = \frac{AH}{AD}=\frac{7,690}{9,6} \approx 0,8010\)
\(\Rightarrow \widehat{D} \approx 53^0\)

