Giải bài 30 trang 89 - Sách giáo khoa Toán 9 tập 1

Đề bài

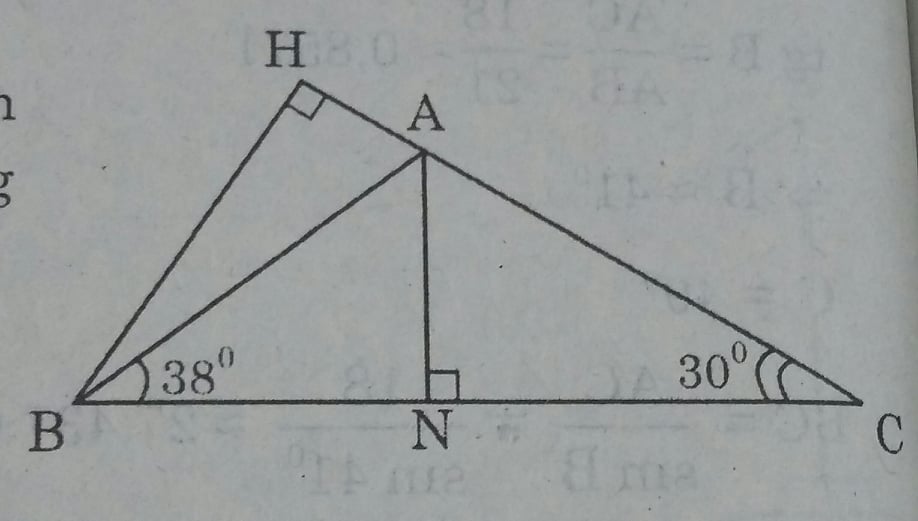
    Cho tam giác ABC, trong đó BC = 11cm, ∠ABC = 38o, ∠ACB = 30o. Gọi điểm N là chân của đường vuông góc kẻ từ A đến cạnh BC. Hãy tính:

   a) Đoạn thẳng AN

   b) Cạnh AC

Hướng dẫn giải

   Hướng dẫn: 

- vẽ thêm đường cao BH.

- Vận dụng hệ thức giữa các cạnh và các góc của tam giác vuông để tính độ dài AN và AC:

   b=a.sin B= a.cos C

   c=a.sin C=a.cos B 

      Giải:

   Kẻ \( BH \perp AC\)

   Xét tam giác vuông BHC có:

   BH= BC.sin C= \(11.sin30^0=5,5(cm)\)

   \( \widehat{HBC}=90^0 - \widehat{HCB}=60^0 \Rightarrow \widehat{HBA}=22^0\)

   Xét tam giác vuông HBA có: 

   \(AB= \frac{BH}{cos\widehat{BHA} }= \frac{5,5}{cos22^0} \approx 5,932(cm)\)

     a) Xét tam giác vuông ABN có: AN= AB.\(sin 38^0 \approx 3,625(cm)\)

     b) Xét tam giác vuông ANC có: \(AC= \frac{AN}{sin C}= 7,304(cm) \)