Khối đa diện và bộ công thức tính thể tính đa diện không thể bỏ qua
Khối đa diện và bộ công thức tính thể tính đa diện không thể bỏ qua
Lý thuyết về khối đa diện và công thức tính thể tích khối là một trong các kiến thức cơ bản nhất mà chúng ta thường hay sử dụng trong các bài tập hình học không gian, tuy nhiên bạn gặp khó khăn trong việc ghi nhớ công thức cũng chưa biết cách giải nhanh các bài tập dạng này. Nhằm giúp các bạn hiểu rõ hơn về phần kiến thức này, chúng tôi đã tổng hợp các công thức cần thiết mời bạn cùng đón đọc.
I. Khái niệm về khối đa diện
Là khối gồm một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện:
- Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
- Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.
Khối phân chia không gian thành hai phần (phần bên trong và phần bên ngoài). Hình đa diện cùng với phần bên trong của nó gọi là khối đa diện.
Mỗi khối sẽ có thể phân chia được thành những khối tứ diện.
II. Phân loại
1. Khối đa diện lồi
Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thằng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện xác định (H) được gọi là đa diện lồi.
2. Khối đa diện đều
Khối đa diện đều là khối hình lồi có tính chất sau đây:
- Mỗi mặt của nó là một đa giác đều p cạnh.
- Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đều như vậy được gọi là khối đa diện đều loại {p ; q}.
Từ định nghĩa trên ta thấy các mặt của khối đều là những đa giác đều bằng nhau
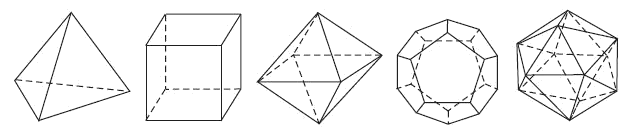
Các loại khối đa diện đều phổ biến:
- Tứ giác đều
- Hình lập phương
- Bát diện đều
- Mười hai mặt đều
- Hai mươi mặt đều
Xem ngay: Công thức tính diện tích tứ giác lồi
III. Công thức tính thể tích khối đa diện
1. Công thức tính thể tích các loại khối đa diện cơ bản
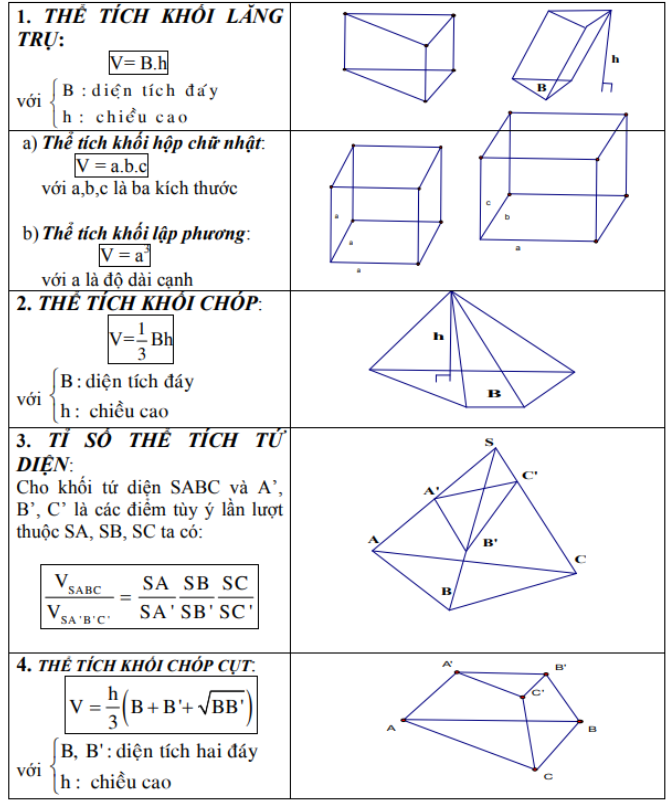
Mới nhất:
2. Các dạng bài tập thể tích khối đa diện
Dạng 1: Thể tích khối lăng trụ đứng có chiều cao hay cạnh đáy
Ví dụ: Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác ABC vuông cân tại A có cạnh \(BC = a \sqrt2\) và biết A'B = 3a. Tính thể tích khối lăng trụ?
Lời giải:
Ta có tam giác ABC vuông cân tại A nên AB = AC = a
ABC A'B'C' là lăng trụ đứng \(\Rightarrow AA' \bot AB \)
\(\Delta AA'B \) vuông tại A nên \(AA'^2=A'B^2-AB'^2=8a^2 \Rightarrow AA' = 2a\sqrt2 \)
Vậy \(V=B.h=S_{ABC}.AA'=a^3\sqrt2\).
Dạng 2: Lăng trụ đứng có góc giữa đường thẳng và mặt phẳng
Ví dụ: Cho lăng trụ đứng tam giác ABC A'B'C' có đáy ABC là tam giác vuông cân tại B với BA = BC = a ,biết A'B hợp với đáy ABC một góc 60 độ . Tính thể tích lăng trụ?
Lời giải:
Ta có \(AA' \bot (ABC )\Rightarrow A'A\bot AB \) và AB là hình chiếu của A'B trên đáy ABC.
Vậy góc \([A'B,(ABC)]=ABA'=60^{\circ}\)
Tam giác ABA' vuông tại A nên \(AA'=AB.tan 60=a\sqrt3\)
\(S_{ABC} =\dfrac{1}{2}.BA.BC=\dfrac{a^2}{2}\)
Vậy \(V= S_{ABC}.AA'=\dfrac{a^3\sqrt 3}{2}\).
Dạng 3: Thể tích khối chóp có cạnh bên vuông góc với cạnh đáy
Ví dụ: Cho hình chóp SABC có SB = SC = BC = CA = a . Hai mặt (ABC) và (ASC) cùng vuông góc với (SBC). Tính thể tích hình chóp?
Lời giải:
Ta có: \(\left\{\begin{array}{cc}(ABC)\bot (SBC)\\(ASC)\bot (SBc)\end{array}\right. \Rightarrow AC\bot (SBC)\)
Vậy \(V=\dfrac{1}{3}S_{SBC}.AC=\dfrac{1}{3}.\dfrac{a^2\sqrt 3}{4}.a=\dfrac{a^3\sqrt 3}{12}\).
Luyện thêm bài tập tại: Câu hỏi trắc nghiệm về khối đa diện
Bài viết này sẽ giúp các em học sinh ghi nhớ, khắc sâu kiến thức một cách dễ dàng, áp dụng nhanh chóng để tìm ra phương hướng chứng minh giải quyết các dạng bài tập liên quan đến các loại khối đa diện. Chúc các em học tốt ^^!

