Giải bài 63 trang 87 - Sách giáo khoa Toán 7 tập 2

Đề bài

Cho tam giác ABC với AC < AB. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Vẽ các đonạ thẳng AD, AE.

a) Hãy so sánh góc ADC và góc AEB.

b) Hãy so sánh các đoạn thẳng AD và AE.

Hướng dẫn giải

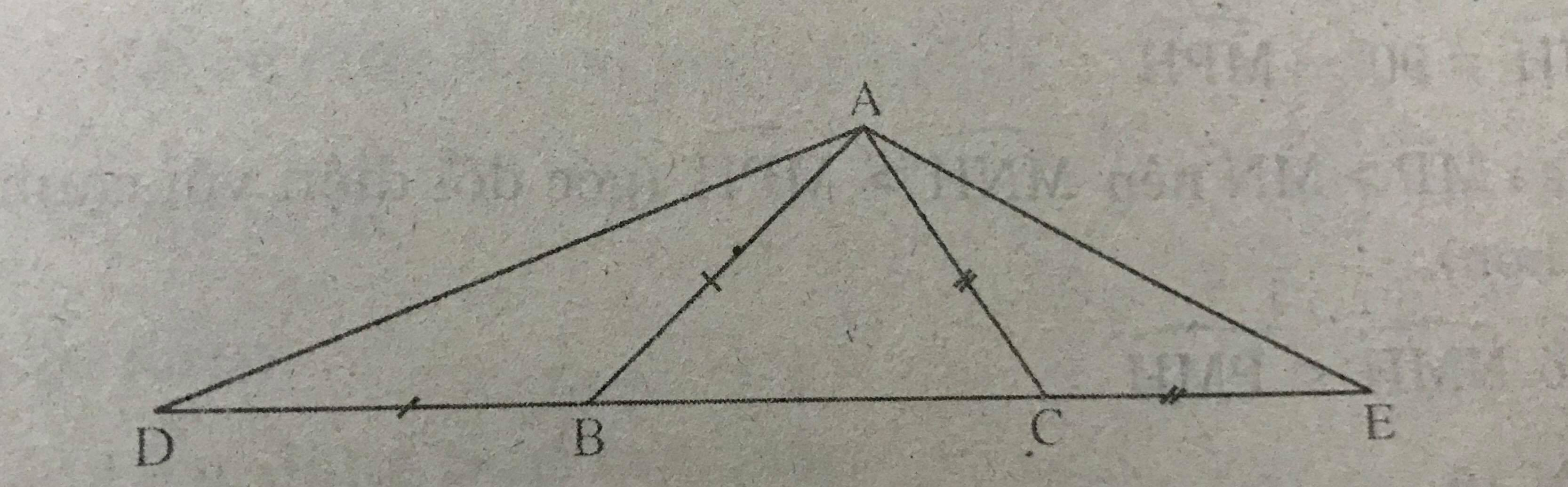
a) Xét tam giác ABC có: AC<AB(gt)

\(\Rightarrow \widehat{ABC}<\widehat{ACB}\,\ (1) \)(quan hệ giữa cạnh và góc đối diện trong tam giác)

Vì AB = BD(gt) \(\Rightarrow \Delta ABD\) cân tại B

\(\Rightarrow \widehat{ADB}=\widehat{DAB}\)

Mà \(\widehat{ABC}=\widehat{ADB}+\widehat{DAB}\) (góc ngoài tam giác ABD)

\(\Rightarrow \widehat{ADB}=\widehat{DAB}=\dfrac{1}{2}.\widehat{ABC}\,\ (2)\)

Chứng minh tương tự với tam giác AEC

\(\Rightarrow \widehat{AEC}=\dfrac{1}{2}.\widehat{ACB}\,\ (3)\)

Từ (1)(2)(3) \(\Rightarrow \widehat{ADC}<\widehat{AEB} (đpcm)\)

b) Xét tam giác ADE có: \(\widehat{ADE}<\widehat{AED}\)  (cmt)

\(\Rightarrow AE < AD\) (quan hệ giữa cạnh và góc đối diện trong tam giác)