Giải bài 45 trang 125 - Sách giáo khoa Toán 7 tập 1

Đề bài

Đố. Cho bốn đoạn thẳng AB, BC, CD, DA trên giấy kẻ ô vuông như ở hình 110. Hãy dùng lập luận để giải thích

a) AB = CD, BC = AD

b) AB // CD

Hướng dẫn giải

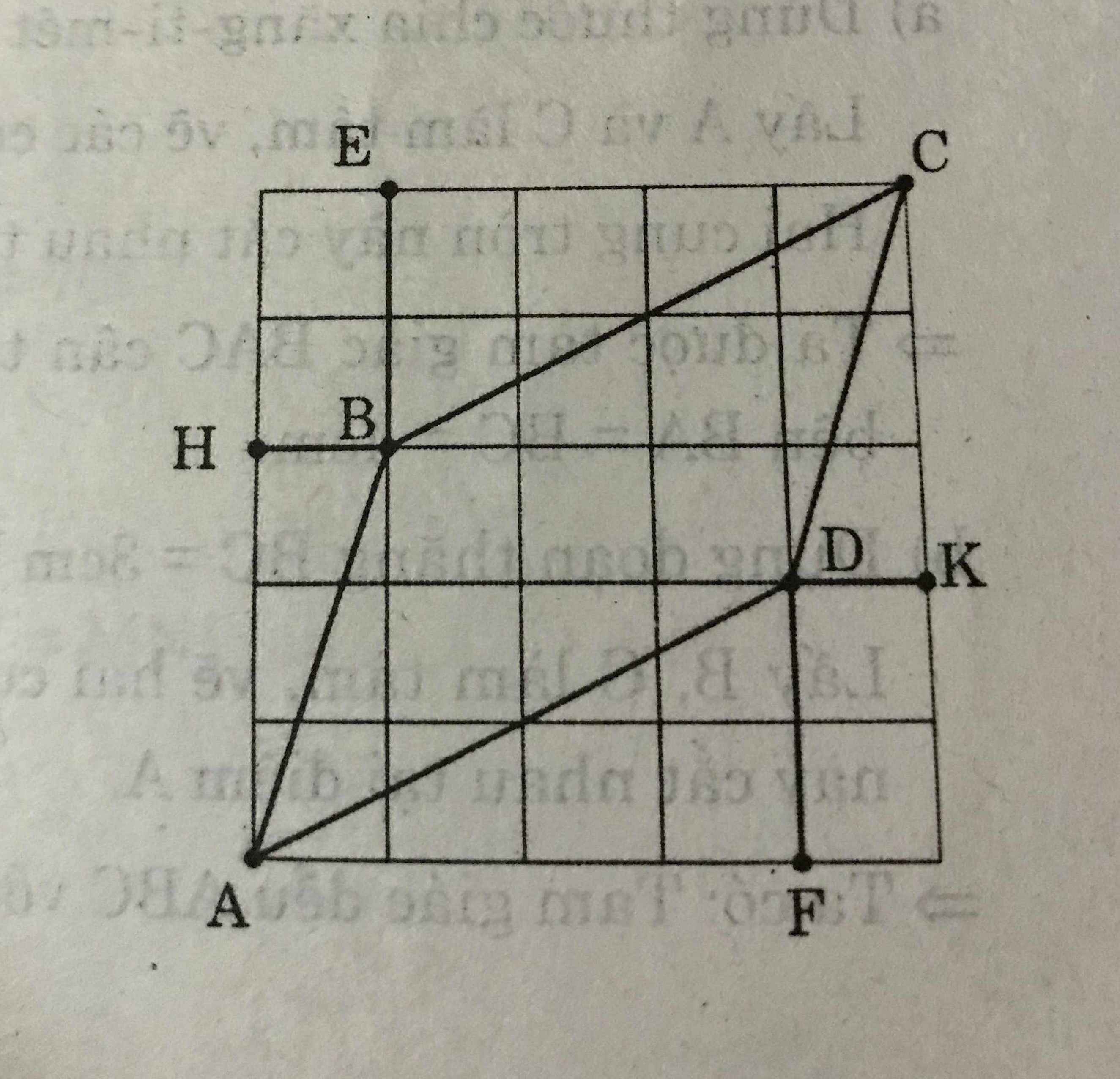
a) Xét ΔAHB và ΔCKD có : 

AH = CK ( = 3 đơn vị dài)

HB = KD ( = 1 đơn vị dài )

\(\widehat{H} = \widehat{K}\) ( = \(90^0\))

Nên  ΔAHB = ΔCKD (c.g.c)

=> AB = CD

Xét ΔCEB và ΔAFD có :

CE = AF ( = 4 đơn vị dài )

BE = DF ( = 2 đơn vị dài )

\(\widehat{E} = \widehat{F} (=90^0)\)

Nên ΔCEB = ΔAFD (c.g.c)

=> BC = AD

b) Xét ΔABD và ΔCDB có :

AB = CD (câu a)

BC = AD (câu a)

BD là cạnh chung

Nên ΔABD = ΔCDB (c.c.c)

=> \(\widehat{ABD} = \widehat{CDB} \)

=> AB // CD (hai góc so le trong bằng nhau)