Giải bài 44 trang 125 - Sách giáo khoa Toán 7 tập 1

Đề bài

 Cho ΔABC có góc B = góc C. Tia phân giác của góc A cắt BC tại D. Chứng minh rằng

a) ΔADB = ΔADC

b) AB = AC

Hướng dẫn giải

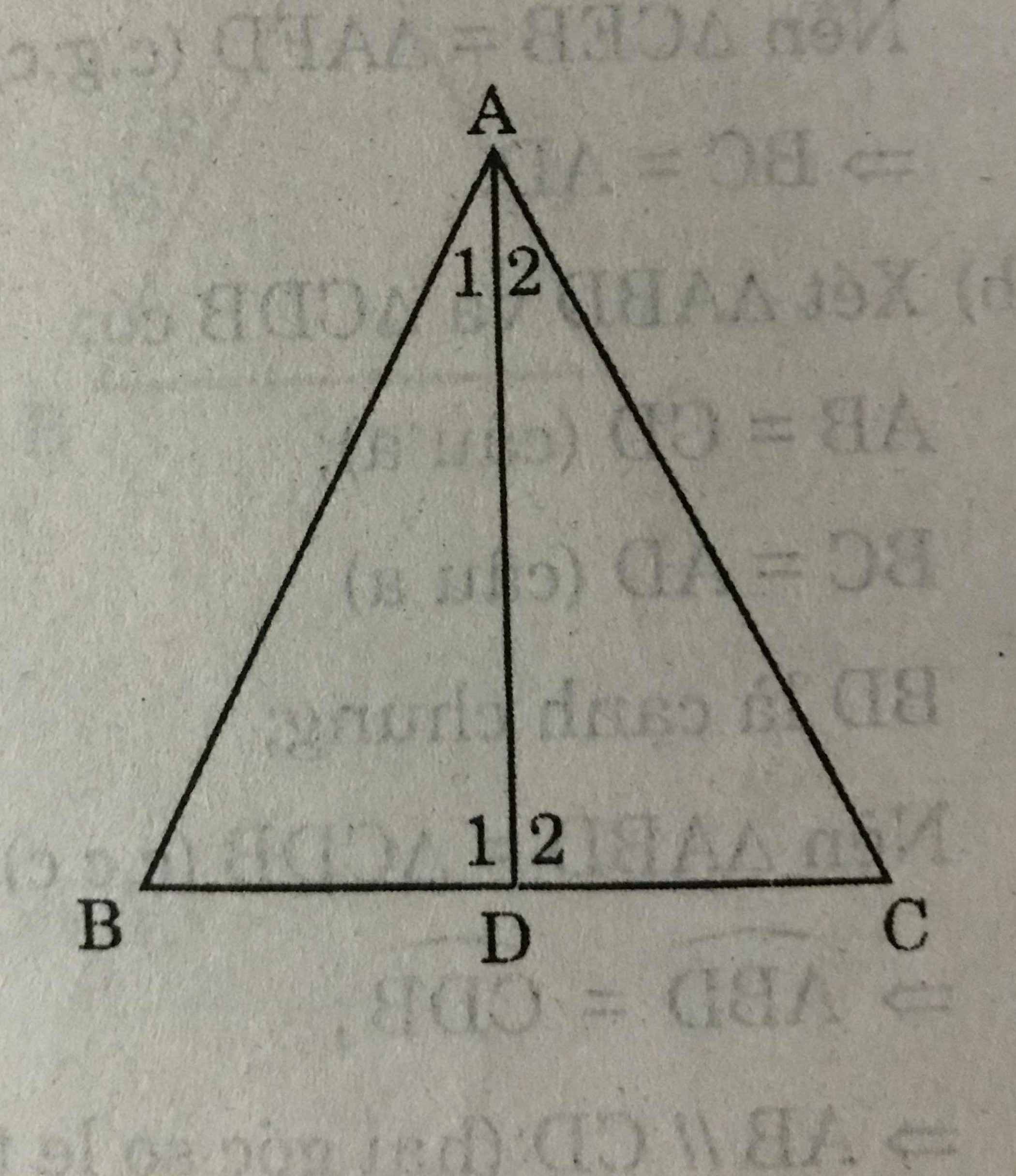
a) AD là tia phân giác của \(\widehat{A}\)

=> \(\widehat{A_1} = \widehat{A_2}\)

Mà \(\widehat{B} = \widehat{C}\) nên \(\widehat{D_1} = \widehat{D_2}\)

ΔABD và ΔACD có :

\(\widehat{B} = \widehat{C}\) (gt)

\(\widehat{D_1} = \widehat{D_2}\)

AD là cạnh chung

Nên ΔABD = ΔACD (g.c.g)

b) ΔABD = ΔACD (câu a) => AB = AC