Bài 90 trang 104 SGK Toán 9 tập 2

Đề bài

a) Vẽ hình vuông cạnh $4cm$.

b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính $R$ của đường tròn này.

c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính $r$ của đường tròn này.

Hướng dẫn giải

+) Đường tròn ngoại tiếp hình vuông là đường tròn đi qua tất cả các đỉnh của hình vuông.

+) Đường tròn nội tiếp hình vuông là đường tròn tiếp xúc với tất cả các cạnh của hình vuông.

Lời giải chi tiết

a) Dùng êke ta vẽ hình vuông $ABCD$ có cạnh bằng $4cm$ như sau:

- Vẽ $AB = 4cm$.

- Vẽ $BC \bot AB$ và $BC = 4cm$

- Vẽ $DC\bot BC$ và $DC = 4cm$

- Nối $D$ với $A$, ta có $AD\bot DC$ và $AD = 4cm$

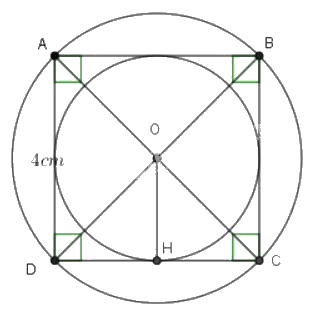
b)Ta có ABCD là hình vuông. Gọi O là giao điểm của 2 đường chéo AC và BD khi đó ta có: OA = OB = OC = OD. Nên O chính là tâm của đường tròn ngoại tiếp hình vuông.

Tam giác $ABC$ là tam giác vuông cân nên $AB = BC$.

Áp dụng định lí Pytago trong tam giác vuông $ABC$, ta có:

$\eqalign{ & A{C^2} = A{B^2} + B{C^2} = 2{\rm{A}}{B^2} \Leftrightarrow A{C^2} = {2.4^2} = 32 \cr & \Rightarrow AC = \sqrt {32} = 4\sqrt 2 \cr}$

Vậy $AO = R = {{AC} \over 2} = {{4\sqrt 2 } \over 2} = 2\sqrt 2$ 

Vậy $R  = 2\sqrt{2}$ $cm$

c) Vẽ $OH \bot DC$.Tương tự ta kẻ từ O các đường vuông góc đến các cạnh AD, AB, BC. Khi đó ta có

Đường tròn tâm $O$, bán kính $OH$. Đó là đường tròn nội tiếp hình vuông $ABCD$

Ta có: $OH = {{A{\rm{D}}} \over 2} = 2(cm)$  

Vậy $r = OH = 2cm$