Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 3 - Hình học 9
Đề bài
Bài 1: Trên tiếp tuyến tại A của đường tròn (O; R), lấy đoạn \(AI = R\sqrt 3 \).
a) Tính độ dài OI theo R.
b) Đường cao AH của ∆OAI cắt đường tròn (O) tại B. Chứng tỏ IB là tiếp tuyến của (O).
Bài 2: Cho đường tròn (O; R) và một điểm A ở ngoài đường tròn sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC đến đường tròn ( B, C là hai tiếp điểm). Từ B vẽ đường thẳng song song với AC cắt (O) tại D ( D khác B). Đường thẳng AD cắt (O) tại E ( khác D).
a) Chứng minh: \(AB^2 = AE.AD\)
b) Chứng minh: \(BC.EC = AC.BE\)
c) Tính khoảng cách giữa hai đường thẳng BD và AC theo R.
Hướng dẫn giải
Bài 1:
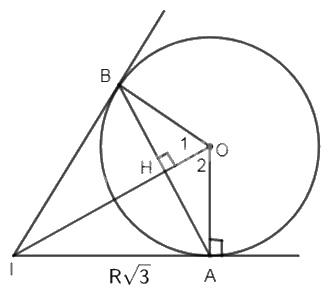
a) ∆OAI vuông tại A ( tính chẩt tiếp tuyến)
Ta có: \(OI = \sqrt {O{A^2} + A{I^2}} = \sqrt {{R^2} + {{\left( {R\sqrt 3 } \right)}^2}} = 2R\).
b) Có \(OH \bot AB\) (gt) nên H là trung điểm của AB ( định lí đường kính dây cung)
∆AOB cân có đường cao OH đồng thời là đường trung tuyến nên \(\widehat {{O_1}} = \widehat {{O_2}}\)
Xét ∆OBI và ∆OAI có :
+) OI cạnh chung,
+) \(\widehat {{O_1}} = \widehat {{O_2}}\) (cmt),
+) \(OB = OA ( = R)\)
Vậy \(∆OBI = ∆OAI\) (c.g.c) \(\Rightarrow \widehat {OBI} = \widehat {OAI} = 90^\circ \)
Chứng tỏ OB là tiếp tuyến của (O).
Bài 2:
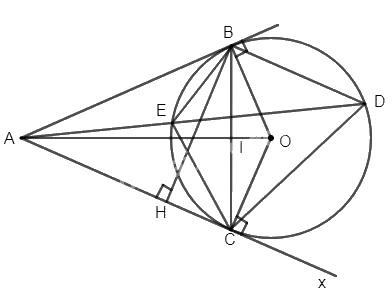
a) Ta có \(\widehat {ABE} = \widehat {BDE}\) ( góc giữa tiếp tuyến và một dây bằng góc nội tiếp cùng chắn cung EB)
Do đó ∆ABE và ∆ADB đồng dạng (g.g)
\( \Rightarrow \dfrac{{AD} }{ {AB}} = \dfrac{{AB} }{{AE}}\)
\( \Rightarrow A{B^2} = AE.AD\)
b) Nối CD.
Khi đó \(\widehat {DCx} = \widehat {CED}\) (góc giữa tiếp tuyến và một dây bằng góc nội tiếp cùng chắn cung CD)
BD // AC \( \Rightarrow \widehat {DCx} = \widehat {BDC}\) ( so le trong)
Do đó \(\widehat {BDC} = \widehat {CED}\) mà \(\widehat {CED} + \widehat {CEA} = 180^\circ \) và \(\widehat {BDC} + \widehat {BEC} = 180^\circ \) ( tổng hai góc đối của tứ giác BECD nội tiếp) \( \Rightarrow \widehat {CEA} = \widehat {BEC}\).
Lại có \(\widehat {EBC} = \widehat {ECA}\) (góc nội tiếp bằng góc giữa tiếp tuyến và một dây cùng chắn cung EC)
Do đó ∆BEC và ∆CEA đồng dạng (g.g)
\( \Rightarrow \dfrac{{BC}}{{AC}} = \dfrac{{BE} }{ {EC}}\)
\(\Rightarrow BC.EC = AC.BE\).
c) Gọi BH là khoảng cách giữa hai đường thẳng song song BD và AC.
Xét tam giác vuông ACO, ta có :
\(AC = \sqrt {A{O^2} - C{O^2}} = \sqrt {{{\left( {3R} \right)}^2} - {R^2}} \)\(\, = R\sqrt 8 \)
Gọi I là giao điểm của AO và BC ta có AO là đường trung trực của đoạn BC nên AO ^ BC tại I hay CI là đường cao của tam giác vuông ACO ta có : CI.AO = CA.CO ( hệ thức lượng)
\( \Rightarrow CI = \dfrac{{CA.CO} }{ {AO}} = \dfrac{{R\sqrt 8 .R} }{ {3R}} =\dfrac {{R\sqrt 8 } }{ 3} \)
\(\Rightarrow BC = {{2R\sqrt 8 } \over 3}\)
Xét tam giác vuông AIC ta có :
\(AI = \sqrt {A{C^2} - C{I^2}} \)\(\,= \sqrt {{{\left( {R\sqrt 8 } \right)}^2} - {{\left( {{{R\sqrt 8 } \over 3}} \right)}^2}} = {{8R} \over 3}\)
Hai tam giác vuông AIC và BHC có \(\widehat {ACI}\) chung nên :
∆AIC và ∆BHC đồng dạng (g.g)
\( \Rightarrow \dfrac{{BH} }{ {AI}} =\dfrac {{BC}}{ {AC}}\)
\( \Rightarrow BH = \dfrac{{AI.BC} }{ {AC}} = \dfrac{{{{8R} \over 3}.{{2R\sqrt 8 } \over 3}}}{ {R\sqrt 8 }} \)\(\,= \dfrac{{{{16{R^2}\sqrt 8 } \over 9}} }{{R\sqrt 8 }} = \dfrac{{16R}}{ 9}\)
Lưu ý : Ta có thể tính khoảng cách CK ( K là giao điểm của CO với BD).

