Tổng kết lý thuyết hình cầu, thể tích hình cầu là gì?

Trong bài viết này Cunghocvui sẽ gửi đến các bạn những kiến thức lý thuyết về hình cầu là gì, thể tích hình cầu, diện tích hình cầu,... Phần cuối sẽ là các dạng bài tập và bài tập luyện tập giúp bạn củng cố kiến thức.

A. Lý thuyết

I. Hình cầu

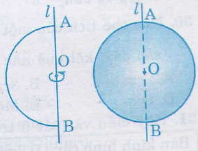
Quay nửa đường tròn tâm O, có bán kính R quanh đường kính AB cố định thì ta được một hình cầu. Thì khi đó:

• Tâm của hình cầu là điểm O
• Bán kính của hình cầu có độ dài R
• Nửa đường tròn ở phép quay trên tạo thành mặt cầu.

II. Diện tích mặt cầu

\(S = 4\pi R^2 = \pi d^2\)

Trong đó:

- S là diện tích mặt cầu

- R là bán kính

- d là đường kính mặt cầu

III. Thể tích hình cầu

\(V = \dfrac {4}{3}\pi R^3\)

Trong đó:

- V là thể tích hình cầu

- R là bán kính

B. Bài tập hình cầu, thể tích hình cầu, diện tích hình cầu (có đáp án)

Câu 1: Quay tam giác ABC vuông cân tại A quanh cạnh AB, biết rằng cạnh AB = a, cung tròn BC có tâm A bán kính a. Hỏi phần khối cầu nằm ngoài khối nón bằng bao nhiêu?

A. \(2\pi a^3\)

B. \(\dfrac {2\pi a^3}{3}\)

C. \(\dfrac {\pi a^3}{3}\)

D. 2\(\pi a^3\)

=> Đáp án đúng: C

=> Lý giải chi tiết:

- Thể tích của khối cầu được sinh ra sau khi quay tam giác ABC quanh cạnh AB là: V = \(\dfrac {1}{2}.\dfrac {4}{3}\pi R^3= \dfrac {2}{3}\pi a^3\)

- Thể tích của hình nón sinh ra sau khi quay tam giác ABC quanh cạnh AB là: V = \(\dfrac {1}{3}S.h= \dfrac {1}{3}\pi R^2=\dfrac {1}{3}\pi a^3\)

- Vậy phần khối cầu nằm ngoài khối nón có thể tích là: V = \(\dfrac {2}{3}\pi a^3 - \dfrac {1}{3}\pi a^3=\dfrac {1}{3}\pi a^3\)

Câu 2: Hình cầu có số đo diện tích mặt cầu được tính bằng đơn vị \(dm^2\) và bằng với số đo thể tích hình cầu(\(dm^3\)). Vậy diện tích của mặt cầu sẽ bằng bao nhiêu?

A. 36\(\pi\) (\(dm^2\))

B. 30\(\pi\) (\(dm^2\))

C. 26\(\pi\) (\(dm^2\))

D. 20\(\pi\) (\(dm^2\))

=> Đáp án đúng: A

=> Lý giải chi tiết:

- Gọi bán kính của hình cầu, diện tích mặt cầu, thể tích hình cầu lần lượt là R, S, V.

- Do số đo diện tích mặt cầu bằng với số đo thể tích hình cầu nên \(4\pi R^2 = \dfrac {4}{3}\pi R^3 \Leftrightarrow R=3 (dm)\)

- Vậy theo công thức tính diện tích mặt cầu trên là: \(S = 4\pi R^2 = 4\pi 3^2 = 36\pi (dm^2)\)

Câu 3: Hình cầu có diện tích mặt ầu bằng 64\(\pi (cm^2)\). Hãy tính thể tích hình cầu vừa rồi.

A. \(\dfrac {32}{3}\pi\)

B. \(64\pi\)

C. \(\dfrac{256}{3}\pi\)

D. \(265\pi\)

=> Đáp án đúng: C

=> Lý giải chi tiết: Áp dụng công thức tính thể tích hình cầu \(V = \dfrac {4}{3}\pi R^3\) 

Câu 4: Hình cầu có số đo diện tích mặt cầu được tính bằng đơn vị \(dm^2\) và bằng với số đo thể tích hình cầu(\(dm^3\)). Vậy thể tích ch của mặt cầu sẽ bằng bao nhiêu? 

A. 36\(\pi\) (\(dm^3\))

B. 30\(\pi\) (\(dm^3\))

C. 26\(\pi\) (\(dm^3\))

D. 20\(\pi\) (\(dm^3\))

=> Đáp án đúng: A

=> Lý giải chi tiết:

- Gọi bán kính của hình cầu là R, diện tích mặt cầu là S, thể tích hình cầu là V

- Do số đo diện tích mặt cầu bằng với số đo thể tích hình cầu nên \(4\pi R^2 = \dfrac {4}{3}\pi R^3 \Leftrightarrow R=3 (dm)\)

- Vậy theo công thức tính thể tích mặt cầu trên là: \(V = \dfrac {4}{3}\pi R^3= \dfrac {4}{3}\pi 3^3=36\pi (dm^3)\)

Câu 5: Quả bóng có hình cầu bán kính 13cm lăn xuống một rãnh có chiều rộng bằng 24cm. Hỏi quả bóng sẽ bị hạ thấp xuống bao nhiêu centimet khi bóng lăn xuống rãnh?

A. 9 (cm)

B. 8 (cm)

C. 7 (cm)

D. 6 (cm)

=> Đáp án đúng: B

=> Lý giải chi tiết: 

- Đường cao OH = \(\sqrt{13^2 - 12^2} = 5\)

- Vậy quả bóng sẽ bị hạ thấp: 13 - 5 = 8 (cm)

Câu 6: Diện tích mặt cầu sẽ tăng gấp bao nhiêu lần nếu bán kính của hình cầu tăng gấp hai lần?

A. Hai lần

B. Bốn lần

C. Sáu lần

D. Tám lần

=> Đáp án đúng: B

Câu 7: Thể tích của hình cầu sẽ tăng gấp bao nhiêu lần nếu bán kính của hình cầu tăng gấp hai lần?

A. Sáu lần

B. Tám lần

C. Bốn ần

D. Sáu lần

=> Đáp án đúng: B

Câu 8: Cho một hình lập phương, bên trong hình lập phương đó được đặt vừa khít một hình cầu. Hỏi rằng phần thể tích hình lập phương nằm trong hình cầu với phần thể tích hình lập phương nằm ngoài hình cầu, phần nào lớn hơn (hay nhỏ hơn)?

A. Nhỏ hơn

B. Lớn hơn

C. Bằng nhau

D. Một đáp án khác

=> Đáp án đúng: B

=> Lý giải chi tiết:

- Gọi độ dài cạnh của hình lập phương đã cho là 1

- Bán kính hình cầu bằng 1/2.

- Thể tích của hình cầu sẽ là \(\dfrac {4}{3}\pi (\dfrac{1}{2})^3 = \dfrac {\pi}{6}>\dfrac {1}{2}\)

Vậy phần thể tích hình lập phương nằm trong hình cầu lớn hơn so với phần thể tích hình lập phương nằm ngoài hình cầu.

Xem thêm >>>  Giải bài tập toán 9 bài Hình cầu, thể tích hình cầu - SGK

Trên đây là toàn bộ những kiến thức lý thuyết về hình cầu, thể tích hình cầu, diện tích hình cầu, các câu bài tập trắc nghiệm mà Cunghocvui muốn gửi đến các bạn học, mong rằng bài viết sẽ giúp ích được nhiều cho quá trình học tập của các bạn. Chúc các bạn học tập tốt <3