Giải bài 54 trang 63 - Sách giáo khoa Toán 9 tập 2
Đề bài
Vẽ đồ thị của hai hàm số:
Hướng dẫn giải
Lập bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| \(y= \dfrac{1}{4}x^2\) | 1 | \(\dfrac{1}{4}\) | 0 | \(\dfrac{1}{4}\) | 1 |
| \(y= -\dfrac{1}{4}x^2\) | -1 | -\(\dfrac{1}{4}\) | 0 | - \(\dfrac{1}{4}\) | -1 |
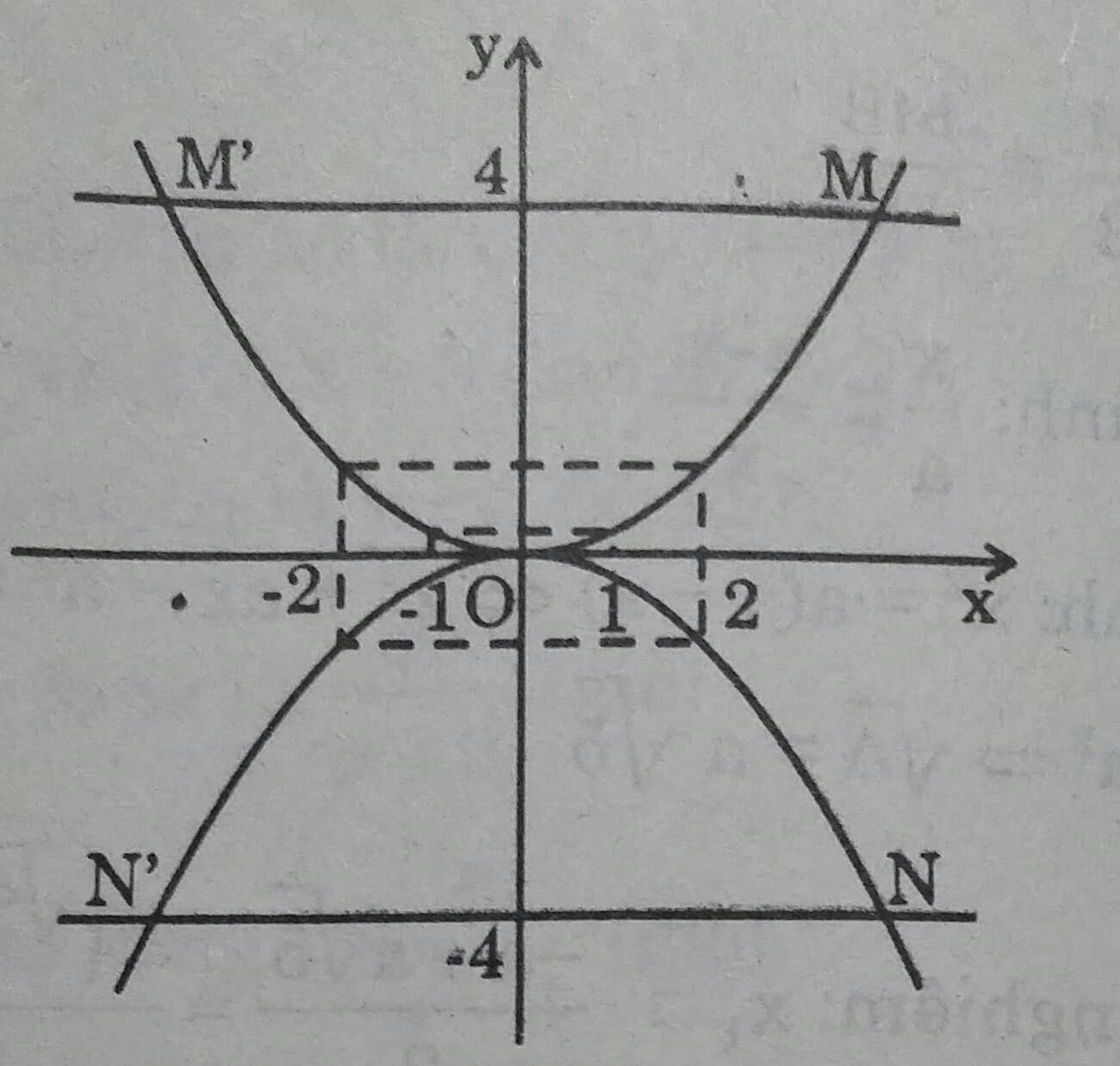 a) Hoành độ của M và M' thỏa mãn phương trình:
a) Hoành độ của M và M' thỏa mãn phương trình:
\(\dfrac{1}{4}x^2= 4 \Leftrightarrow x = \pm 4\)
M( 4;4); M'(-4;4).
b) N' đối xứng với M' qua Ox nên N'(-4;-4).
N đối xứng với M qua Ox nên N(4;-4).
Đường thẳng NN' song song với Ox vì N, N' thuộc đường thẳng y =-4.
Tìm tung độ N theo công thức
\(y = - \dfrac{1}{4}x^2 = - \dfrac{1}{4}4^2 = -4\)

