Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 2 - Hình học 9
Đề bài
Bài 1. Cho ∆ABC có ba góc nhọn nội tiếp đường tròn (O), các đường cao BE, CF cắt nhau tại H.
a. Chứng minh bốn điểm B, F, E, C thuộc cùng một đường tròn.
b. Kẻ đường kính AA’ của đường tròn (O). Chứng minh tứ giác BHCA’ là hình bình hành.
Bài 2. Cho đường tròn (O), dây AB không qua tâm O. Vẽ dây AC vuông góc với AB tại A. Chứng tỏ B, O, C thẳng hàng.
Hướng dẫn giải
Bài 1.
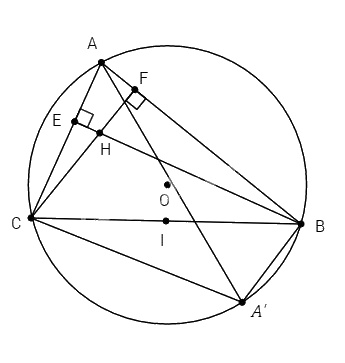
a. Gọi I là trung điểm của BC. Các tam giác vuông BFC và BEC lần lượt có các trung tuyến là IF và IE nên:
\(\eqalign{ & IF = IE = {1 \over 2}BC \cr & hay\,IB = IF = IE = IC \cr} \)
Chứng tỏ bốn điểm B, F, E, C thuộc cùng một đường tròn tâm I là trung điểm của BC.
b. Ta có: ∆ABA’ nội tiếp đường tròn có đường kính AA’ nên ∆ABA’ vuông tại B hay AB ⊥ A’B.
Lại có CH ⊥ AB (gt)
Do đó CH // A’B. Chứng minh tương tự ta có: AH // A’C
Vậy tứ giác BHCA’ là hình bình hành.
Lưu ý: Chứng minh tương tự như câu a, chúng ta sẽ có bốn điểm A, F, H, E thuộc cùng một đường tròn.
Bài 2.
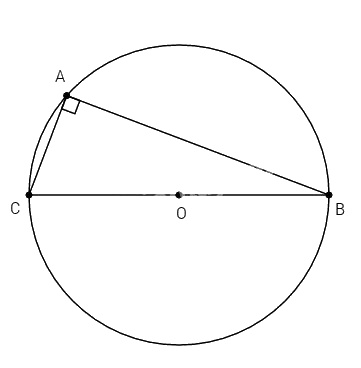
Ta có: AB ⊥ AC (gt) nên ∆ABC là tam giác vuông nội tiếp đường tròn (O). Do đó BC là đường kính của đường tròn (O) nên BC đi qua O. Hay ba điểm B, O, C thẳng hàng.

