Cực trị của hàm số - Tổng hợp lý thuyết không nên bỏ qua

KIẾN THỨC CẦN NHỚ VỀ CỰC TRỊ 

I. Cực trị hàm số

1. Cực trị là gì?

Giả sử hàm số \(f\) xác định và liên tục trên khoảng \((a; b)\) và điểm \(x_o \in (a; b)\).

a) Nếu \(f(x) < f(x_o)\) với mọi \(x \in (a; b)\)\  \(\begin{Bmatrix}x_o\end{Bmatrix}\) thì \(x_o\) là một điểm cực đại của hàm số. 

Khi đó \(f(x_o)\) được gọi là giá trị cực đại của hàm số \(f\).

b) Nếu \(f(x) > f(x_o)\) với mọi \(x \in (a; b)\) \  \(\begin{Bmatrix}x_o\end{Bmatrix}\) thì \(x_o\) là một điểm cực tiểu của hàm số. 

Khi đó \(f(x_o)\) được gọi là giá trị cực tiểu của hàm số \(f\).

Điểm \(M(x_o; f(x_o))\) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số. 

Các điểm cực đại và điểm cực tiểu gọi chung là điểm cực trị. 

Giá trị cực đại và giá trị cực tiểu còn gọi là cực đại (cực tiểu) và gọi chung là cực trị của hàm số. 

2. Điều kiện để hàm số có cực trị 

a) Điều kiện cần 

Định lý 1:

Nếu hàm số \(y = f(x)\) có đạo hàm trên khoảng \( (a; b)\) và đạt cực đại hoặc cực tiểu tại \(x_o\) thì \(f'(x_o) = 0\).

Chú ý: Đạo hàm \(f'\) có thể bằng 0 tại điểm \(x_o\) nhưng hàm số \(f\) không đạt cực trị tại điểm \(x_o\).

Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm. 

b) Điều kiện đủ 

Định lý 2: 

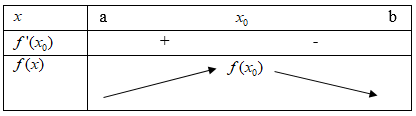
Nếu hàm số \(f\) xác định và liên tục trên khoảng \((a; x_o)\) và \(f'(x_o) < 0\) trên khoảng \((x_o; b)\) thì \(x_o\) là một điểm cực đại của hàm số \(f(x)\).

- Nếu \(f'(x_o)\) trên khoảng \((a; x_o)\) và \(f'(x_o) < 0\) trên khoảng \((x_o; b)\) thì \(x_o\) là một điểm cực đại của hàm số \(f(x)\).

Có thể nói, nếu \(f'(x_o)\) đổi dấu từ dương sang âm khi \(x\) đi qua điểm \(x_o\) thì hàm số đạt cực đại tại \(x_o\). 

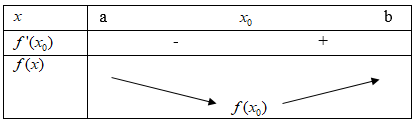
- Nếu \(f'(x_o) < 0 \) trên khoảng \((a; x_o)\) và \(f'(x_o) > 0\) trên khoảng \((x_o; b)\) thì \(x_o\) là điểm cực tiểu của hàm số \(f(x)\).

Có thể nói, nếu \(f'(x_o)\) đổi dấu từ âm sang dương khi \(x\) đi qua điểm \(x_o\) thì hàm số đạt cực tiểu tại \(x_o\).

3. Quy tắc tìm cực trị của hàm số

Định lý 3: 

Giả sử hàm số \(f\) có đạo hàm cấp hai trên khoảng \((a; b)\) với mọi \(x_o \in (a; b)\). Khi đó: 

- Nếu \(f'(x_o) = 0, f''(x_o) > 0 \) thì \(x_o\) là điểm cực tiểu. 

- Nếu \(f'(x_o) = 0, f''(x_o) < 0 \)thì \(x_o\) là điểm cực đại. 

Quy tắc: 

- Quy tắc 1: Áp dụng định lý 2 

+ Tìm tập xác định. 

+ Tính \(f'(x)\). Tìm các điểm \(x_i (i = 1, 2, 3,...)\) tại đó \(f'(x) = 0\) hoặc \(f'(x)\) không xác định. 

+ Lập bảng biến thiên. 

+ Xét dấu \(f'(x)\), nếu \(f'(x)\) đổi dấu khi \(x\) qua điểm \(x_i\) thì hàm số đạt cực trị tại điểm \(x_i\).

- Quy tắc 2: Áp dụng định lý 3

+ Tìm tập xác định. 

+ Tính \(f'(x)\). Tìm các điểm \(x_i (i = 1, 2, 3,...)\)của phương trình \(f'(x) = 0\).

+ Tính \(f''(x_i)\).

Nếu \(f''(x_i) < 0\) thì hàm số đạt cực đại tại \(x_i\).

Nếu \(f''(x_i) > 0\) thì hàm số đạt cực tiểu tại \(x_i\).

II. Cực trị số phức

1. Phương pháp đại số 

a) Bất đẳng thức tam giác 

\(\begin{vmatrix}z_1 + z_2 \end{vmatrix} \leq \begin{vmatrix}z_1\end{vmatrix} +\begin{vmatrix}z_2\end{vmatrix}\), dấu "=" xảy ra khi \(z_1 = kz_2\) với \(k \geq 0\).

\(\begin{vmatrix}z_1 - z_2 \end{vmatrix} \leq \begin{vmatrix}z_1\end{vmatrix} +\begin{vmatrix}z_2\end{vmatrix}\), dấu "=" xảy ra khi \(z_1 = kz_2\) với \(k \leqslant 0\).

\(\begin{vmatrix}z_1 + z_2 \end{vmatrix} \geqslant \begin{vmatrix}\begin{vmatrix}z_1\end{vmatrix} -\begin{vmatrix}z_2\end{vmatrix}\end{vmatrix}\), dấu "=" xảy ra khi \(z_1 = kz_2\) với \(k \leqslant 0\).

\(\begin{vmatrix}z_1 - z_2 \end{vmatrix} \geq \begin{vmatrix}\begin{vmatrix}z_1\end{vmatrix} -\begin{vmatrix}z_2\end{vmatrix}\end{vmatrix}\), dấu "=" xảy ra khi \(z_1 = kz_2\) với \(k \geq 0\).

b) Công thức trung tuyến: 

\(\begin{vmatrix}z_1 + z_2\end{vmatrix}^2 + \begin{vmatrix}z_1 - z_2\end{vmatrix}^2 = 2(\begin{vmatrix}z_1 \end{vmatrix}^2 + \begin{vmatrix}z_2\end{vmatrix}^2)\)

2. Phương pháp hình học 

Phương pháp tập hợp điểm: 

\(\begin{vmatrix}z - (a + bi)\end{vmatrix} = r\): Đường tròn tâm I(a; b) bán kính r. 

\(\begin{vmatrix}z - (a_1 + b_1i)\end{vmatrix} = \begin{vmatrix}z - (a_2 + b_2i)\end{vmatrix}\): Đường trung trực AB với \(A(a_1; b_1), B(a_2; b_2)\).

\(\begin{vmatrix}z - (a_1 + b_1i)\end{vmatrix} + \begin{vmatrix}z - (a_2 + b_2i)\end{vmatrix} = 2a\); 

- Đoạn thẳng AB với \(A(a_1; b_1), B(a_2; b_2)\) nếu \(2a = AB\). 

- Elip \((E)\) nhận \(A, B\) làm hai tiêu điểm với độ dài trục lớn là \(2a\) nếu \(2a > AB\). 
Đặc biệt: \(\begin{vmatrix}z + c \end{vmatrix} + \begin{vmatrix}z - c\end{vmatrix} = 2a\). Elip \((E)\): \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\) với \(b = \sqrt{a^2 - c^2}\).

Sau khi học xong lý thuyết, các em tham khảo các dạng bài tập tại cunghocvui.com.