Bài 97 trang 105 SGK Toán 9 tập 2

Đề bài

Cho tam giác \(ABC\) vuông ở \(A\). Trên \(AC\) lấy một điểm \(M\) và vẽ đường tròn đường kính \(MC\). Kẻ \(BM\) cắt đường tròn tại \(D\). Đường thẳng \(DA\) cắt đường tròn tại \(S\). Chứng minh rằng:

a) \(ABCD\) là một tứ giác nội tiếp;

b) \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{D}}}\) ;

c) \(CA\) là tia phân giác của góc \(SCB\)

Hướng dẫn giải

Một số dấu hiệu nhận biết tứ giác nội tiếp

- Tứ giác có tổng hai góc đối bằng \({180^0}\)

- Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.

- Tứ giác có 4 đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác.

- Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới 1 góc \(\alpha \)

Lời giải chi tiết

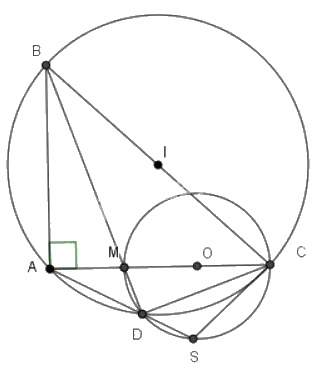
a) Ta có góc \(\widehat {MDC}\) là góc nội tiếp chắn nửa đường tròn \((O)\) nên \(\widehat {MDC} = {90^0}\)

⇒ \(∆CDB\) là tam giác vuông nên nội tiếp đường tròn đường kính \(BC\).

Ta có \(∆ABC\) vuông tại \(A\).

Do đó \(∆ABC\) nội tiếp trong đường tròn tâm \(I\) đường kính \(BC\).

Ta có \(A\) và \(D\) là hai đỉnh kề nhau cùng nhìn \(BC\) dưới một góc \(90^0\) không đổi nên tứ giác \(ABCD\) nội tiếp đường tròn đường kính \(BC\)

b) Ta có \(\widehat {AB{\rm{D}}}\) là góc nội tiếp trong đường tròn \((I)\) chắn cung \(AD\).

Tương tự góc \(\widehat {AC{\rm{D}}}\) là góc nội tiếp trong đường tròn \((I)\) chắn cung \(AD\)

Vậy \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{D}}}\)

c) Ta có:

\(\widehat {ADB} + \widehat {BDS} = {180^0}\) ( 2 góc kề bù)

Mà \(\widehat {MCS} + \widehat {MDS} = {180^0}\) (tứ giác CMDS nội tiếp đường tròn (O))

Từ đó ta có: \(\widehat {ADB}=\widehat {MCS}\) (1)

Lại có tứ giác ABCD nội tiếp nên \(\widehat {ADB}=\widehat {ACB}\) (2)

Từ (1) và (2) ta suy ra \(\widehat {MCS}=\widehat {ACB}\)

Vậy tia \(CA\) là tia phân giác của góc \(SCB\)