Bài 87 trang 100 SGK Toán 9 tập 2

Đề bài

Lấy cạnh \(BC\) của một tam giác đều làm đường kính, vẽ một nửa đường tròn về cùng một phía với tam giác ấy đối với đường thẳng \(BC\). Cho biết cạnh \(BC = a\), hãy tính diện tích hình viên phân được tạo thành.

Hướng dẫn giải

+) Sử dụng các công thức tính hình quạt tròn và diện tích tam giác đều.

+) Diện tích hình viên phân = Diện tích cung tròn \(MqB\) - Diện tích tam giác \(OMB.\)

Lời giải chi tiết

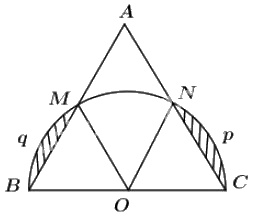
Gọi nửa đường tròn tâm \(O\) đường kính \(BC\) cắt hai cạnh \(AB\) và \(AC\) lần lượt tại \(M\) và \(N\).

\(∆ONC\) có \(OC = ON, \, \,  \widehat{C} = 60^0\) nên \(∆ONC\) là tam giác đều, do đó \(\widehat{NOC} = 60^0.\)

\(S_{quạt \, \, NOC} = \frac{\pi \left ( \frac{a}{2} \right )^{2}.60^{\circ}}{360^{\circ}} = \frac{\pi a^{2}}{24}\).

\(S_{\Delta NOC} = \frac{\left ( \frac{a}{2} \right )^{2}\sqrt{3}}{4}= \frac{a^{2}\sqrt{3}}{16}\)

Diện tích hình viên phân: 

\({S_{CpN}} = \frac{{\pi {a^2}}}{{24}} - \frac{{{a^2}\sqrt 3 }}{{16}} = \frac{{{a^2}}}{{48}}\left( {2\pi  - 3\sqrt 3 } \right).\)

Vậy diện tích hai hình viên phhân bên ngoài tam giác là:

            \(S=2.{S_{CpN}}=\frac{a^{2}}{24}\left ( 2\pi -3\sqrt{3} \right ).\)