Giải bài 84 trang 99 - Sách giáo khoa Toán 9 tập 2
Đề bài
a) Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1cm. Nêu cách vẽ.
b) Tính diện tích miền gạch sọc.
Hướng dẫn giải
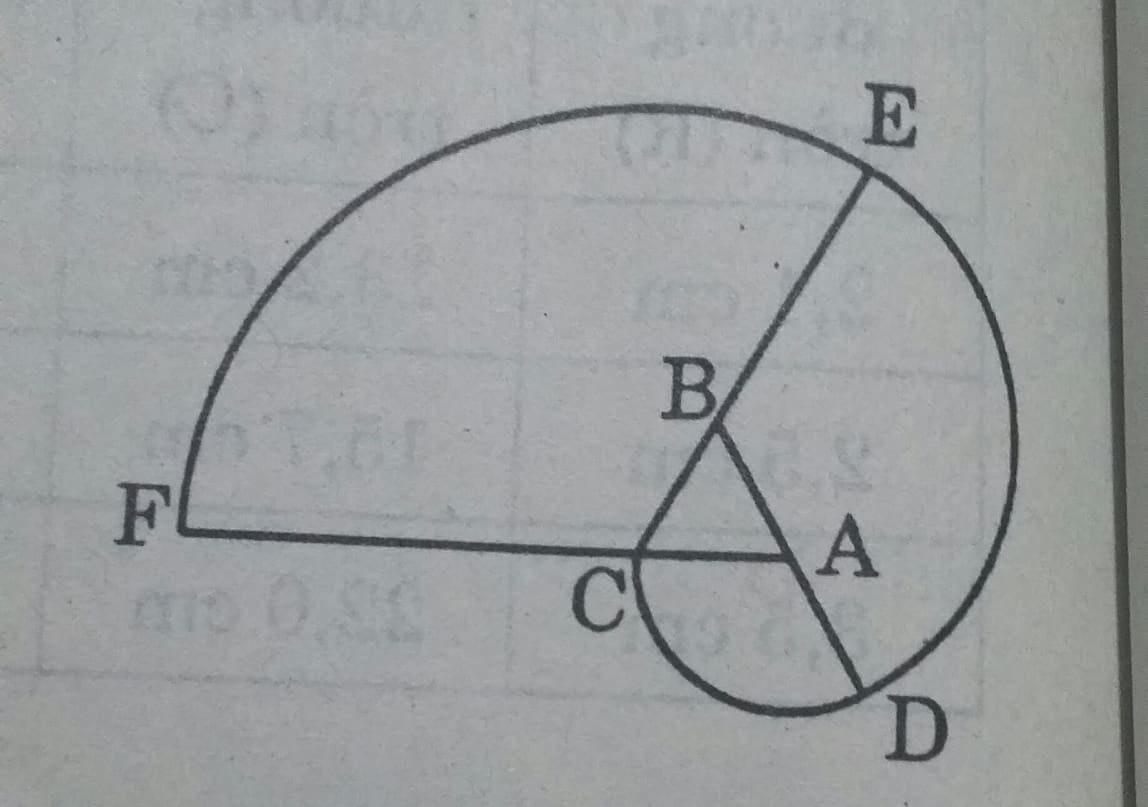
a) Vẽ tam giác đều ABC cạnh 1cm.
Vẽ cung CD có tâm A, bán kính 1 cm( D thuộc tia đối của tia AB)
Vẽ cung DE có tâm B, bán kính 2cm ( E thuộc tia đối của tia BC)
Vẽ cung EF có tâm C, bán kính 3 cm ( F thuộc tia đối của tia CA)
b) Diện tích miền gạch sọc là tổng diện tích của ba hình quạt.
Diện tích hình quạt ACD là: \(S_1 = \dfrac{1}{3}\pi 1^2= \dfrac{1}{3}\pi (cm^2)\)
Diện tích hình quạt BDE là: \(S_2 = \dfrac{1}{3}\pi 2^2= \dfrac{4}{3}\pi (cm^2)\)
Diện tích hình quạt CEF là: \(S_3= \dfrac{1}{3}\pi 3^2=3\pi (cm^2)\)
Diện tích phần gạch sọc là là:
\(S= S_1 + S_2 + S_3 = \dfrac{14}{3}\pi (cm^2)\)

