Bài 75 trang 96 SGK Toán 9 tập 2
Đề bài
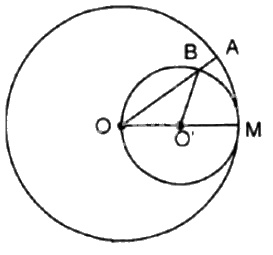
Cho đường tròn \((O)\), bán kính \(OM\). Vẽ đường tròn tâm \(O'\), đường kính \(OM\). Một bán kính \(OA\) của đường tròn \((O)\) cắt đường tròn \((O')\) ở \(B\).
Chứng minh cung \(MA\) và cung \(MB\) có độ dài bằng nhau.
Hướng dẫn giải
+) Góc nội tiếp có số đo bằng nửa số đo cung bị chắn.
+) Góc ở tâm có số đo bằng số đo cung bị chắn.
+) Độ dài cung \(n^0\) của đường tròn bán kính \(R\) là: \(l=\frac{\pi Rn}{180}.\)
Lời giải chi tiết
Đặt \(\widehat {MOB} = \alpha \)
\(\Rightarrow \widehat {MO'B} = 2\alpha\) (góc nội tiếp và góc ở tâm của đường tròn \((O’)\) cùng chắn cung \(BM\)).
Ta có: \(\widehat{BO'M}\) là góc ở tâm chắn cung \(BM \Rightarrow sđ\overparen{MB}= 2\alpha. \)
\(\Rightarrow\) Độ dài cung \(MB\) là:
\({{l_\overparen{MB}}} = {{\pi .O'M.2\alpha } \over {{{180}^0}}} = {{\pi .O'M.\alpha } \over {{{90}^0}}}(1)\)
Ta có: \(\widehat{AOM}\) là góc ở tâm chắn cung \(AM \Rightarrow sđ\overparen{AM}= \alpha. \)
\(\Rightarrow\) Độ dài cung \(MA\) là:
\({{l_\overparen{MA}}} = {{\pi .OM.\alpha } \over {{{180}^0}}} = {{2\pi .O'M.\alpha } \over {{{180}^0}}} = {{\pi O'M.\alpha } \over {{{90}^0}}}(2)\)
(Vì \(OM = 2O’M\))
Từ (1) và (2) \(\Rightarrow {l_\overparen{MB}}={l_\overparen{MA}}\).

