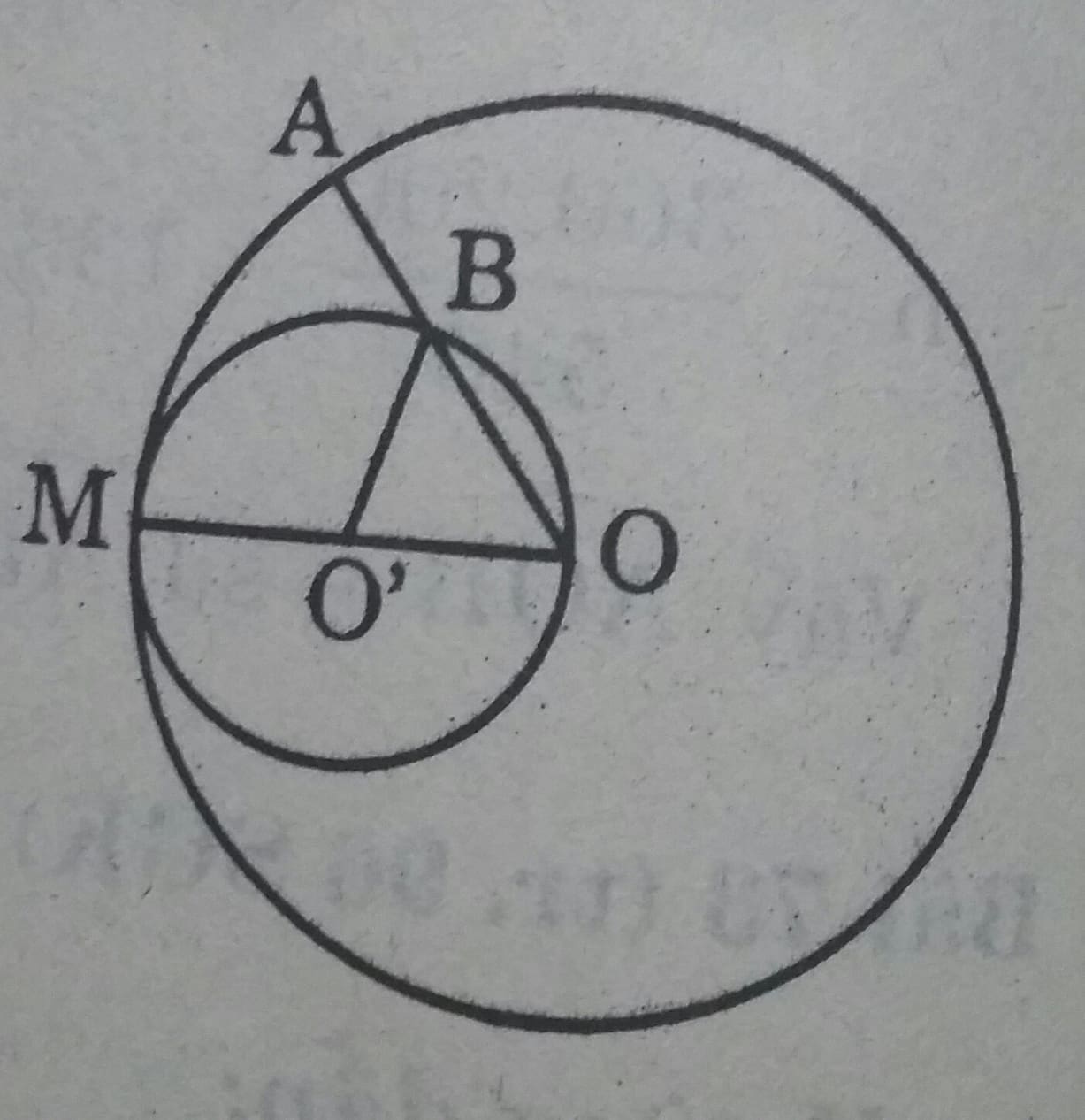Giải bài 75 trang 96 - Sách giáo khoa Toán 9 tập 2

Đề bài

   Cho đường tròn (O), bán kính OM. Vẽ đường tròn tâm O', đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.

Hướng dẫn giải

   Ta có \(\widehat{MOB}= \dfrac{1}{2} \widehat{MO'B}\) ( góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung).

  Giả sử

 \(\widehat{MOB}=x^0 \ thì \ \widehat{MO'B}= 2.x^0 \\ Suy \ ra \ sd \stackrel\frown{MA} = x^0 ; sd \stackrel\frown{MB}= 2.x^0.\\ Ta có l_{ \stackrel\frown{MA}}= \dfrac{\pi.OM.x}{180 } \ (1)\\ l_{ \stackrel\frown{MB}}= \dfrac{\pi.O'M.x}{180 }= \dfrac{\pi.OM.x}{180 }( vì \ OM = 2.O'M) (2)\\Từ \ (1) \ và (2) \ suy \ ra\ l_{ \stackrel\frown{MA}}=l_{ \stackrel\frown{MB}}\)