Bài 22 trang 76 SGK Toán 9 tập 2

Đề bài

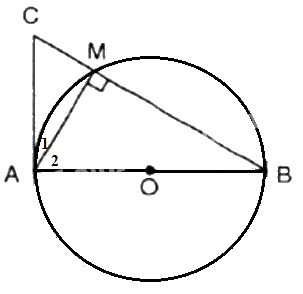
Trên đường tròn \((O)\) đường kính \(AB\), lấy điểm \(M\) (khác \(A\) và \(B\)). Vẽ tiếp tuyến của (O) tại \(A\). Đường thẳng \(BM\) cắt tiếp tuyến đó tại \(C\). Chứng minh rằng ta luôn có: \(M{A^2} = MB.MC\)

Hướng dẫn giải

Ta có: \(\begin{array}{l}
\widehat {{A_2}} + \widehat B = {90^0};\widehat C + \widehat B = {90^0} \Rightarrow \widehat {{A_2}} = \widehat C\\
\widehat {{A_1}} + \widehat {{A_2}} = {90^0};\widehat {{A_2}} + \widehat B = {90^0} \Rightarrow \widehat {{A_1}} = \widehat B
\end{array}\)

Ta có: \(∆MAB\) đồng dạng \(∆MCA\)  (\(\widehat{A_{2}}\) = \(\widehat{C}\); \(\widehat{B}\) = \(\widehat{A_{1}}\))

nên \(\frac{MA}{MB}\) = \(\frac{MC}{MA}\)

Suy ra  \(M{A^2} = MB.MC\)