Bài 21 trang 76 SGK Toán 9 tập 2
Đề bài
Cho hai đường tròn bằng nhau \((O)\) và \((O')\) cắt nhau tại \(A\) và \(B\). Vẽ đường thẳng qua \(A\) cắt \(O\) tại \(M\) và cắt \((O')\) tại \(N\) ( \(A\) nằm giữa \(M\) và \(N\)). Hỏi \(MBN\) là tam giác gi? Tại sao?
Hướng dẫn giải
Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Lời giải chi tiết
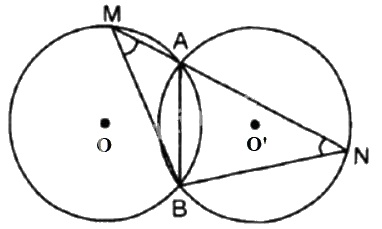
Do hai đường tròn bằng nhau nên hai cung nhỏ \(\overparen{AB}\) bằng nhau. Vì cùng căng dây \(AB\).
Suy ra \(\widehat N = \widehat M\) (cùng chắn hai cung bằng nhau) nên tam giác \(BMN\) là tam giác cân đỉnh \(B\)

