Giải bài 26 trang 76 - Sách giáo khoa Toán 9 tập 2
Đề bài
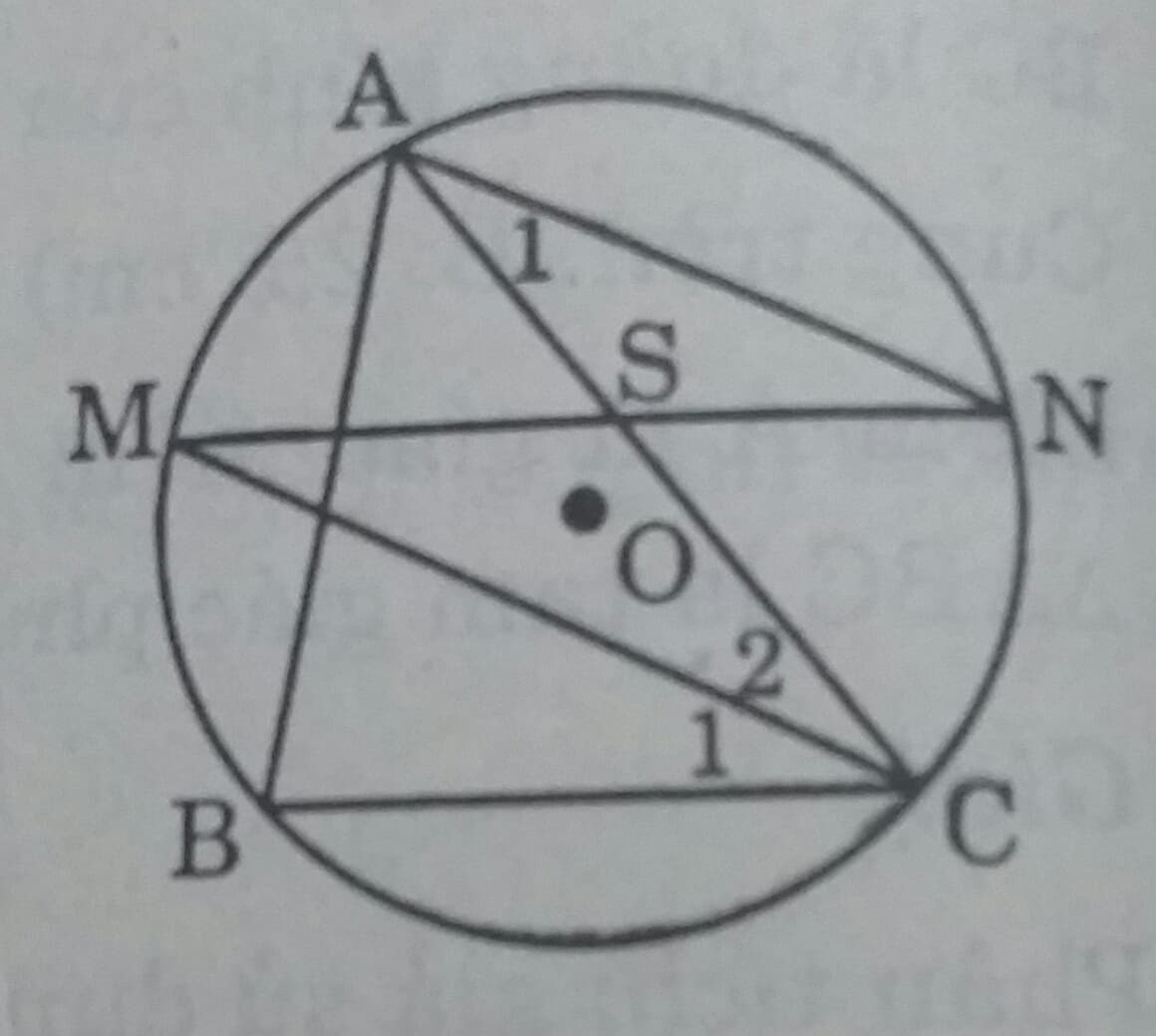
Cho AB, BC, CA là ba dây của đường tròn (O). Từ điểm chính giữa M của cung AB vẽ dây MN song song với dây BC.Gọi giao điểm của MN và AC là S.Chứng minh SM = SC và SN = SA.
Hướng dẫn giải
Ta có MN// BC
\(\Rightarrow \widehat{SMC}= \widehat{C_1}\\ \stackrel\frown{MA}= \stackrel\frown{MB} \Rightarrow \stackrel\frown{C_2}= \stackrel\frown{C_1}\)
( hai góc nội tiếp cùng chắn hai cung bằng nhau)
Suy ra \( \widehat{SMC}= \widehat{C_2} \Rightarrow \Delta SMC \)( cân tại S \(\Rightarrow SM = SC\))
Ta có \(\widehat{A_1}= \widehat{SMC}\)( hai góc nội tiếp cùng chắn cung \(\stackrel\frown{CN}\))
Ta có \(\widehat{C_2}= \widehat{ANM}\)( hai góc nội tiếp cùng chắn cung AM)
Vì \(\widehat{SMC}= \widehat{C_2}\) ( chứng minh trên) nên \(\widehat{A_1}= \widehat{ANM}\)
Suy ra \(\Delta SAN \ cân \ tại \ S \Rightarrow SN = SA\)