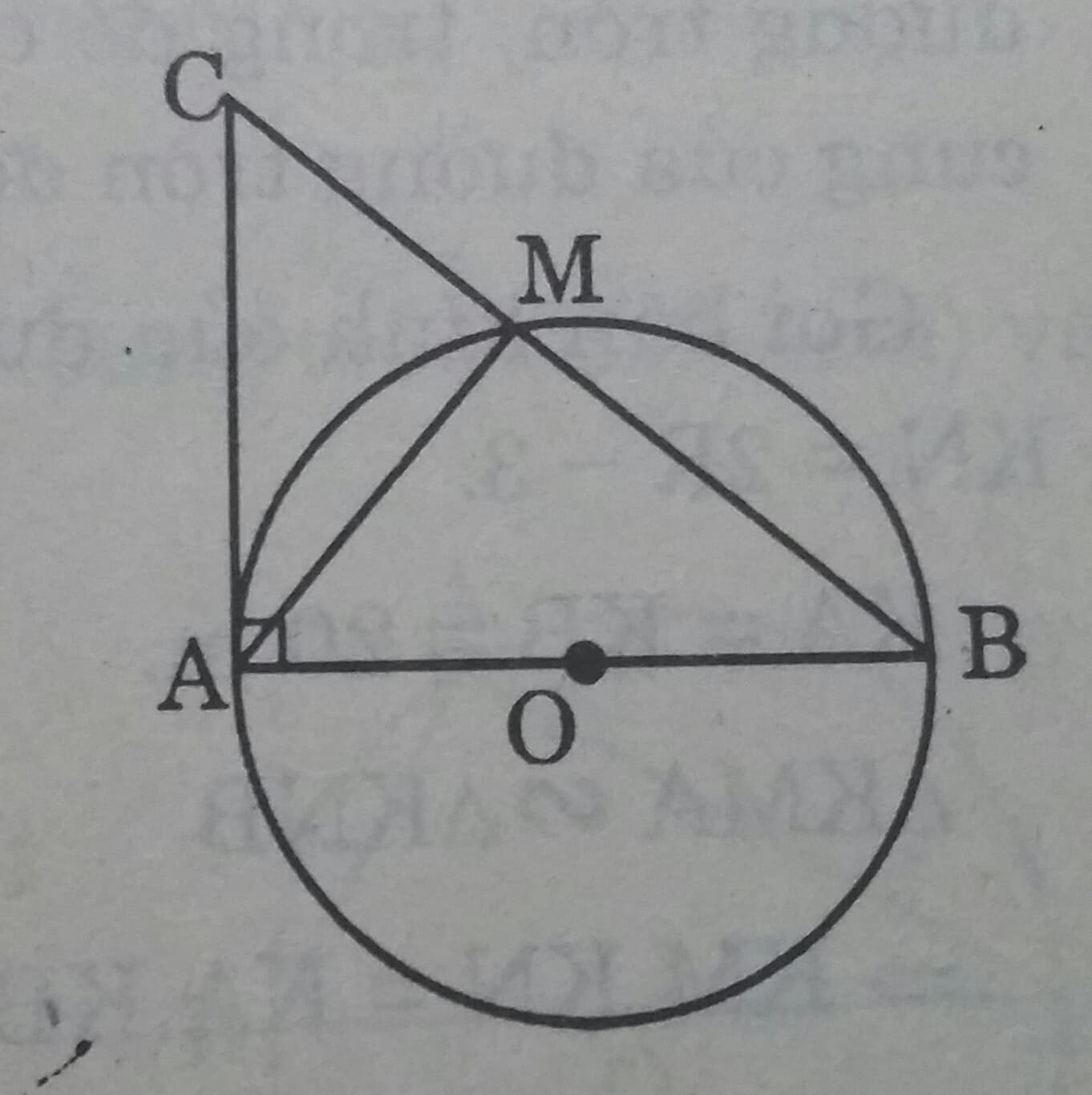Giải bài 22 trang 76 - Sách giáo khoa Toán 9 tập 2

Đề bài

      Trên đường tròn (O) đường kính AB, lấy điểm M (khác A và B). Vẽ tiếp tuyến của (O) tại A. Đường thẳng BM cắt tiếp tuyến đó tại C. Chứng minh rằng ta luôn có:

$MA^2 = MB . MC$

Hướng dẫn giải

   Ta có $AC \perp AB$( tính chất của tiếp tuyến)

   $\widehat{AMB}= 90^0$ ( góc nội tiếp chắn nữa đường tròn đường kính AB) $\Rightarrow AM \perp BC$

   Do đó $\Delta ABC$ vuông tại A, và AM là đường cao của tam giác

   Áp dụng hệ thức lượng $h^2 = b'.c'$ vào tam giác vuông ABC ta được:   $MA^2= MB.MC$