Giải bài 24 trang 76 - Sách giáo khoa Toán 9 tập 2
Đề bài
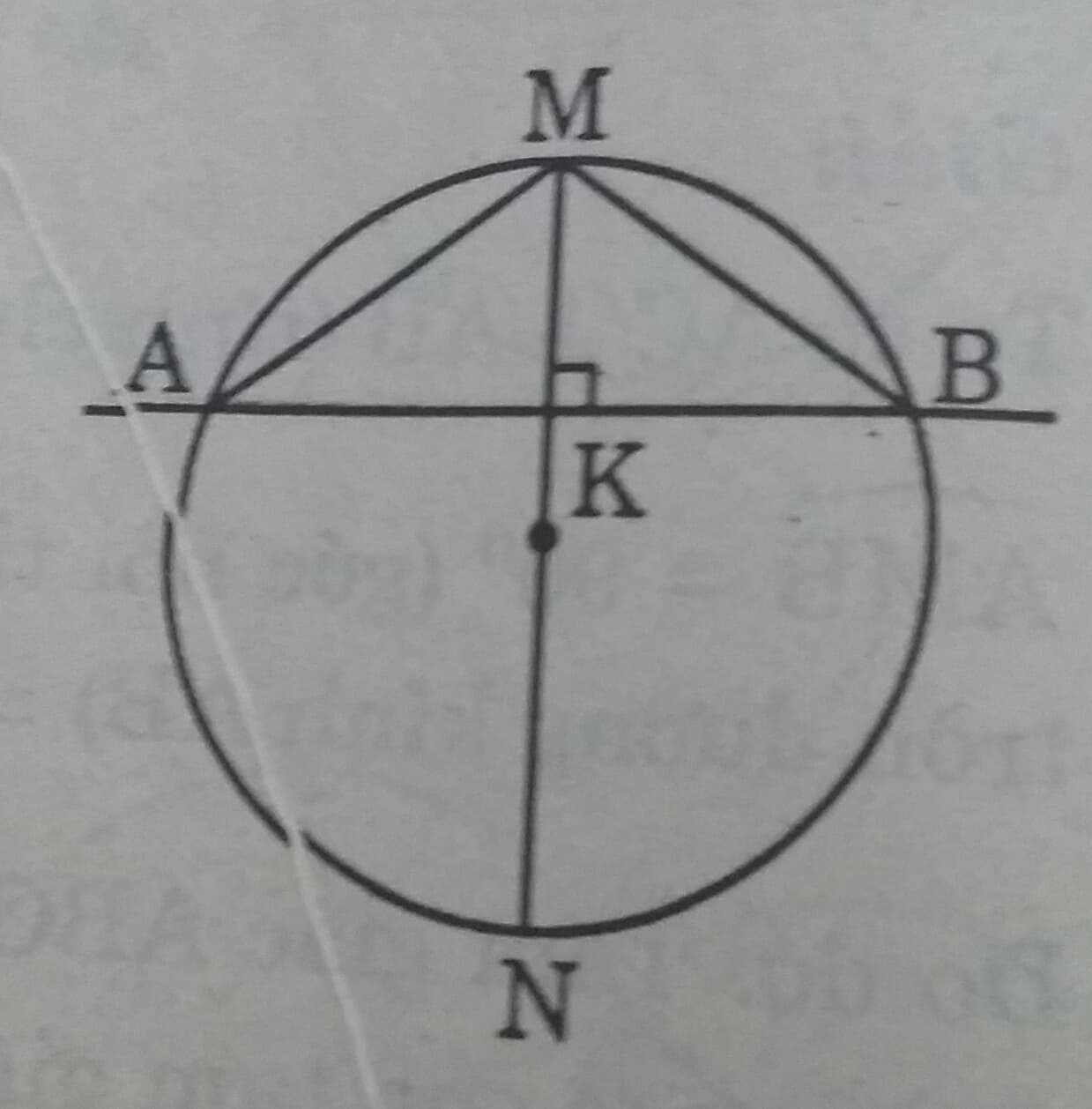
Một chiếc cầu được thiết kế như hình 21 có độ dài AB = 40m, chiều cao MK = 3m. Hãy tính bán kính của đường tròn chứa cung AMB.
Hướng dẫn giải
MK nằm trên đường kính MN của đường tròn, trong đó cung AMB là một cung của nửa đường tròn đó.
Gọi bán kính của đường tròn là R thì KN=MN-MK = 2R-3
Vì \( MN \perp AB \) nên KA= KB = 20m
Xét
\(\Delta KMA \ và \ \Delta KNB \ có :\\ \widehat{MKA}= \widehat{NKB}= 90^0\)
\(\widehat{KAM}= \widehat{KNB}\) ( hai góc nội tiếp cùng chắn cung MB)
Do đó \(\Delta KMA \sim \Delta KNB \Rightarrow KM.KN= KA.KB \Rightarrow3(2R-3)= 20.20 \\\Rightarrow R= 68,2(m)\)