Bài 26 trang 76 SGK Toán 9 tập 2
Đề bài
Cho \(AB, BC, CA \) là ba dây của đường tròn \((O)\). Từ điểm chính giữa \(M\) của \(\overparen{AB}\) vẽ dây \(MN\) song song với dây \(BC\). Gọi giao điểm của \(MN\) và \(AC\) là \(S\). Chứng minh \(SM = SC\) và \(SN = SA\)
Hướng dẫn giải
Ta có:
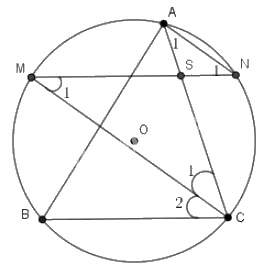
+) Chứng minh SM = SC
\(\widehat {{M_1}} = \widehat {{C_2}}\) (2 góc ở vị trí so le trong)
\(\widehat{{{C}_{1}}}=\widehat{{{C}_{2}}}\) (2 góc nội tiếp chắn 2 cung bằng nhau \(\overset\frown{BM}=\overset\frown{AM}\) )
Nên suy ra \(\widehat{{{M}_{1}}}=\widehat{{{C}_{1}}}\)
Suy ra tam giác SMC là tam giác cân tại S. Vậy SM = SC.
+) Chứng minh SA = SN
Ta có: \(\widehat {{M_1}} = \widehat {{A_1}}\)( 2 góc nội tiếp cùng chắn cung NC)
\(\widehat {{C_1}} = \widehat {{N_1}}\)(2 góc nội tiếp cùng chắn cung AM)
Mà \(\widehat{{{M}_{1}}}=\widehat{{{C}_{1}}}\) (chứng minh trên)
\(\widehat{{{A}_{1}}}=\widehat{{{N}_{1}}}\) (vì cùng bằng 2 góc bằng nhau)
Vậy tam giác SAN cân tại S. Nên SA = SN

