Hình Elip - Phương trình Elip và bộ công thức tính diện tính hình Elip

Hình Elip - Phương trình Elip và bộ công thức tính diện tính hình Elip

Trong hệ thống hình học lớp 10, bạn chắc chắn sẽ không thể bỏ qua nội dung liên quan đến hình Elip. Dưới đây là những kiến thức tổng hợp về phần Elip để bạn có thể lưu lại và trau dồi thêm cho bản thân về mảng hình học ở cấp bậc trung học phổ thông!

I. Định nghĩa

1. Hình Elip là gì?

Cho 2 điểm cố định \(F_1, F_2 \ với \ F_1F_2=2c\)  và một độ dài không đổi \(2a(a>c)\).

Khi đó, Elip là tập hợp những điểm M sao cho:

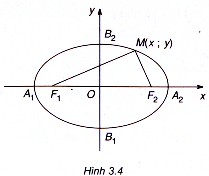
• \(F_1,F_2\): là hại tiêu điểm
• \(F_1F_2=2c\): tiêu cự
• \(F_1M;F_2M\): Bán kính qua tiêu

 

2. Cách vẽ hình Elip

Bước 1: Vẽ 2 đường tròn tâm O qua 2 đường kính AB và CD biết AB là trục dài, CD là trục ngắn

Bước 2: Chia 2 đường tròn thành 12 phần bằng nhau

Bước 3: Từ các điểm 1,2,3.. và 1',2',3' kẻ các đường thẳng song song với trục AB và CD

Khi đó, giao điểm của các đường 1-1',2-2' là các điểm nối thành Elip.

Xem thêm:

• Lý thuyết phương trình đường tròn trong mặt phẳng tọa độ
• Các công thức liên quan đến Elip
• Các công thức Hypebol

3. Đặc điểm hình học

• Elip có hai trục đối xứng (AB, CD trên hình vẽ) vuông góc và cắt nhau tại tâm đối xứng, cắt đường elip tại các trục lớn AB và nhỏ CD. Nửa chiều dài của các trục này được gọi lần lượt là bán trục lớn (a) và bán trục nhỏ (b). Khoảng cách từ tâm e-líp đến mỗi tiêu điểm được gọi là bán tiêu cự (c).

Trong một elip ta luôn có:

\({\displaystyle c^{2}=a^{2}-b^{2}}\)

• Độ dẹt của elíp (hay còn gọi là tâm sai hay độ lệch tâm của elip) là tỉ số giữa tiêu cự và độ dài trục lớn:

\({\displaystyle e={\frac {c}{a}}} \) (0 ≤ e < 1)

e = 0 khi 2 tiêu điểm trùng nhau và hình elíp lúc bấy giờ là hình tròn.

II. Phương trình Elip

Pt Elip như sau:

1. Phương trình chính tắc

Cho hình Elip có tiêu điểm \(F_1 \ và \ F_2\), chọn hệ trục tọa độ Oxy sao cho \(F_1(−c;0), F_2(c;0)\).

Khi đó phương trình chính tắc đường Elip được biểu diễn dưới dạng:

\(M(x;y) \ \in \ elip \ \Rightarrow (E) :\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}= 1\)

Trong đó: \(b^{2}= a^{2}-c^{2}\).

2. Phương trình tham số

Từ phương trình chính tắc của elip, ta có thể suy ra được dạng lượng giác như sau:

\(\left\{\begin{matrix}x = bcos\alpha & \\ y=acos\alpha & \end{matrix}\right.\)

Phương trình đường Elip dạng tham số giúp ta giải quyết được rất nhiều bài toán trong các trường hợp phương trình chính tắc phức tạp hơn. Sở dĩ việc chuyển phương trình về dạng phương trình tham số được sử dụng nhiều là vì nó làm đơn giản hóa bài toán nhờ tính chất của hàm số lượng giác.

3. Phương trình tiếp tuyến

Phương trình tiếp tuyến của (E) với \(M(x_0; y_0) \ \epsilon\ (E): \dfrac{x_0x}{a^2}+\dfrac{y_0y}{b^2}=1\)

Điều kiện tiếp xúc của (E) và Δ: Ax+By+C=0

\(A^2b^2+B^2b^2=C^2\)

Luyện tập tại: Bài tập về phương trình Elip BÀI 3 TRANG 103 SGK HÌNH HỌC 10  BÀI 9 TRANG 99 SGK HÌNH HỌC 10 BÀI 31 TRANG 103 SGK HÌNH HỌC 10 BÀI 1 TRANG 88 SGK HÌNH HỌC 10 BÀI 9 TRANG 93 SGK HÌNH HỌC 10.

III. Công thức tính diện tích Elip

Công thức tính diện tích hình Elip được tính như sau:

\(S=π.a.b\)

Trong đó:

• π là hằng số toán học có giá trị \(π = 3.14159265359\)
• a: nửa chiều dài của trục lớn
• b: nửa chiều dài của trục nhỏ

Công thức Elip trong tính chu vi: \({\displaystyle P=2\pi {\sqrt {\frac {r_{1}^{2}+r_{2}^{2}}{2}}}}\)

Còn về cách xây dựng những công thức tính trên có thể sử dụng phương pháp tính tích phân.

Vừa rồi chúng tôi đã giúp bạn tổng hợp các kiến thức cơ bản về hình Elip và đưa ra các bài tập liên quan có lời giải. Mọi thắc mắc về bài học xin vui lòng để lại dưới mục bình luận, cảm ơn quý bạn đọc đã quan tâm đến bài viết của chúng tôi!