Bài 9 trang 99 SGK Hình học 10

Đề bài

Cho elip \((E)\) có phương trình: \({{{x^2}} \over {100}} + {{{y^2}} \over {36}} = 1\)

a) Hãy xác định tọa độ các đỉnh, các tiêu điểm của elip \((E)\) và vẽ elip đó

b) Qua  tiêu điểm của elip dựng đường thẳng song song với \(Oy\) và cắt elip tại hai điểm \(M\) và \(N\). Tính độ dài đoạn thẳng \(MN\).

Hướng dẫn giải

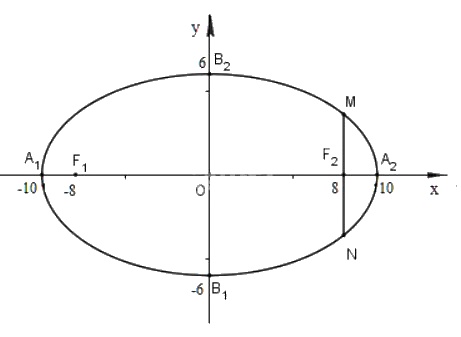
a) Ta có: \(a^2= 100 ⇒ a = 10\)

              \(b^2= 36 ⇒ b = 6\)

              \(c^2= a^2– b^2= 64 ⇒ c = 8\)

Từ đó ta được:

\(A_1(-10; 0), A_2(10; 0), B_1(0; -3), \)\(B_2(0;3), F_1(-8; 0), F_2(8; 0)\)

b) Thế \(x = 8\) vào phương  trình của elip ta được:

 \({{64} \over {100}} + {{{y^2}} \over {36}} = 1 \Rightarrow y =  \pm {{18} \over 5}\)

Ta có: \({F_2}M = {{18} \over 5} \Rightarrow MN = {{36} \over 5}\)